4. THE PHOTON COUNT DISTRIBUTION

Another powerful statistic tool to constrain the nature of the DGRB is provided by the photon count Probability Distribution Function (PDF). This technique can be used when the emission is represent by a pixelated sky-map. The photon count PDF is, then, built from the number of pixels n_k in which k photons are detected. The study of the photon count PDF is commonly used in radio and X-ray astronomy for the analysis of diffuse emissions, in particular when trying to estimate the contribution of faint unresolved sources. It can also be used at gamma-ray frequencies to single out different components in the DGRB, even if they are subdominant. Indeed, different PDFs are expected for different populations of gamma-ray emitters: bright but rare sources generate pixels with a large (or moderately large) number of photons, i.e. n_k will be significantly different from zero even at large k. On the other hand, a population of faint but numerous sources is normally associated with a Poissonian PDF. Intrinsically diffuse emissions also correspond to Poissonian PDFs.

Ref. [69] measures the PDF directly from 11 months of Fermi LAT data between 1 and 300 GeV. The data are binned into a HEALPix map with N_side = 32, corresponding to a binsize of approximately 0.4°. A region of 30° around the Galactic plane is masked, while point sources are not masked. The observed PDF is represented as red data points in Fig. 18. A model based on the so-called generating functions is developed to interpret the data. If p_k is the probability of finding k photons in a certain pixel (i.e. p_k = n_k / N_pixels, where N_pixels is the total number of pixels considered in the analysis), the corresponding generating function P(t) is defined as

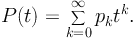(38)

Viceversa, the probabilities p_k can be derived from P(t) as the coefficients in front of each term in the power-law expansion of P(t). The generating function of an emission composed by multiple components is the product of the generating functions of the single components [421]. In particular, the model considered in Ref. [69] consists of 3 terms:

• point sources, both resolved and unresolved. The corresponding generating function is P(t) = exp[∑_m=1^∞(x_m t^m − x_m)], where x_m is the average number of sources emitting exactly m photons in a pixel. The set of {x_m} can be derived from the differential source count distribution dN / dS. In Ref. [69], dN / dS is taken to be a broken power law [18], leaving its 4 parameters free.
• the diffuse Galactic foreground, whose emission, in each pixel, is interpreted as a collection of sources that emit exactly 1 photon. The number of those sources is proportional to the intensity of the foreground in that pixel. Its generating function P(t, i) depends on the particular pixel i considered and it can be written as P(t, i) = exp(x_diffⁱ t − x_diffⁱ), where x_diffⁱ is the number of photons of foreground emission in the i-th pixel. In Ref. [69], the intensity and morphology of the foreground are derived from the Fermi LAT data itself.
• an isotropic component, included to represent the emission associated to faint abundant sources. As for the Galactic foreground, this term is modeled as a collection of x_iso sources emitting exactly 1 photon and its generating function is P(t) = exp(x_iso t − x_iso), for all the pixels. The quantity x_iso is left free in the fit.

The model is fitted to the photon count PDF in Fig. 18 in order to determine the free parameters, i.e. those characterizing dN / dS and the normalization of the isotropic component. The best-fit dN / dS is compatible with what found in Ref. [18]. The analysis of the PDF is different and complementary to Ref. [18] but it succeeds in reconstructing the properties of a population of non-Poissonian blazar-like sources. By integrating the best-fit dN / dS obtained in Ref. [69] below the sensitivity of the Fermi LAT, unresolved blazars are found to account for ∼ 23% of the DGRB reported in Ref. [8] above 1 GeV. We remark that this result is consistent with the independent estimation obtained in Ref. [18]. Similar results are also obtained in Ref. [364] using 5 years of simulated Fermi LAT data and a pixel size of 0.25°.

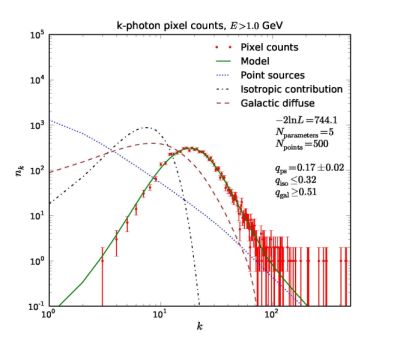Figure 18. nk is the number of pixels with k photons. The red dots correspond to the pixel counts derived from the data of the Fermi LAT, the error bars are equal to √nk. The model devised to interpret the data considers three classes of sources: i) AGN-like point-like objects (blue dotted line), ii) isotropic Poisson contribution (brown dashed line) and iii) anisotropic Galactic diffuse emission (black dash-dotted line). Note that the photon count PDF for the total (solid black line) on this plot is not the sum of the components, but the corresponding generating function of the PDF is the product of the generating functions of the three contributions. Nparameters is the number of parameters used in the fit. qps, qiso and qgal are the relative contributions of the point sources, of the isotropic and of the Galactic foreground, respectively. Npoints is the number of points in the x-axis employed in the fit and the log-likelihood of the best-fit is indicated in the legend. Taken from Ref. [69].

Predictions for the PDF are available not only for blazars: Ref. [36] computed the PDF expected from unresolved MSPs finding that their PDF is highly non-Poissonian.

In the case of DM-induced emission, the shape of the PDF is expected to depend on which DM structures are considered. Ref. [422] computes the probability P(F) of detecting a certain flux F due to Galactic DM subhalos in a generic pixel. The probability depends on the modeling of the subhalo population and, in particular, on the value of M_min. It can be written as follows (see the Appendix of Ref. [422] for a detailed derivation):

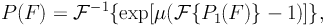(39)

where {f(x)} indicates the Fourier transform of f(x) and ⁻¹ its inverse. The quantity µ is the average number of sources expected inside one pixel and P₁(F) is the probability of having exactly one source emitting the flux F. The DGRB model in Ref. [422] also includes a background component with a Poissonian PDF. The authors prove that there exists a region in their parameter space in which Galactic DM subhalos are faint enough to escape detection as individual sources after 5 years of Fermi LAT data, but bright enough to be detected by studying the photon count PDF.

Ref. [423] also studies the possibility of separating the emission associated with Galactic DM subhalos from the diffuse Galactic foreground and from an isotropic background (both characterized by a Poissonian PDF). The authors choose some benchmark models for the description of the DM-induced emission and of the Poissonian backgrounds. After building the PDFs of the different components, they use them to generate mock sky-maps of the expected gamma-ray emission. This mimics a real observation and it allows to estimate the sensitivity of a PDF analysis to the DM signal. The mock photon count PDF is compared to model predictions in order to determine the free parameters in the model, as done in Ref. [69]. This relies on a a priori knowledge of the shape of the PDF for the different components in the model. Ref. [423] proves that, in an idealized case without background, the reconstructed intensity of the DM-induced emission depends significantly on the assumed shape of the PDF. Employing the wrong PDF would lead to biased reconstruction of the intensity of the DM component. However, when the Poissonian backgrounds are included, Ref. [423] finds that an unbiased reconstruction (within statistical uncertainties) can be obtained independently of the shape of the PDF.

Ref. [424] considered the gamma-ray emission of extragalactic DM halos and subhalos, instead. The authors derive P₁(F) analytically, relying on the halo model, and they show how its shape changes when using three different prescriptions for the subhalo boost. Then, they compute P(F) by means of the central limit theorem below a reference flux F_⋆, and through MC simulations above that. The resulting flux distribution P(E) exhibits two regimes: below 5 × 10⁻¹² cm⁻² s⁻¹ GeV⁻¹ sr⁻¹ it follows a Gaussian distribution, while it is a power law for larger fluxes. ⁴² The latter is the case when a few bright DM structures dominate the flux distribution. Ref. [424] also developed a model for the P(F) of the astrophysical components of the DGRB: for a fiducial subhalo boost model inspired by Ref. [280], the authors of Ref. [424] show that a measurement of {p_k} after 5 years of Fermi LAT data can lead to a detection of a DM signal, provided that the annihilation cross section is, at least, twice the thermal value, for a DM mass of 85 GeV and annihilations into b quarks.

⁴² The gamma-ray flux is computed at 1 GeV. Back.