© CAMBRIDGE UNIVERSITY PRESS 2000

7.2 Expansion of a homogeneous Universe

Because the cosmic background radiation is highly uniform, we infer that the Universe is isotropic - it is the same in all directions. We believe that on a large scale the cosmos is also homogeneous - it would look much the same if we lived in any other galaxy. Then, it can be shown that the length s of a path linking any two points at time t is given by integrating the expression

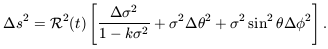
(7.5)

where , , are spherical polar coordinates in an expanding curved space. Apart from their small peculiar speeds, galaxies remain at points with fixed values of those coordinates. The coordinate is dimensionless, while the distance between galaxies expands according to the scale length (t).

Because they follow the galaxies as the Universe expands, , , are called comoving coordinates. The origin = 0 looks like a special point, but in fact it is not. Just as at the Earth's poles where lines of longitude converge, the curvature here is the same as everywhere else, and we can equally well take any point to be = 0. The constant k specifies the curvature of space. For k = 1, the Universe is closed, with positive curvature and finite volume, analogous to the surface of a sphere; (t) is the radius of curvature. If k = -1, we have an open Universe, a negatively curved space of infinite volume, while k = 0 describes familiar unbounded flat space. Near the origin, where >> 1, the formula for s is almost the same for all values of k; on a small enough scale, curvature does not matter. If we look at a tiny region, the relationships among angles, lengths, and volumes will be the same as they are in flat space.

Problem 7.7: In ordinary three-dimensional space, using cylindrical polar coordinates we can write the distance between two nearby points (R, , z) and (R + R, + , z + z) as s2 = R2 + R2 2 + z2. The equation R2 + z2 = 2 describes a sphere of radius : show that if our points lie on this sphere, then the distance between them is   (7.6) where = R / . When k = 1 in Equation 7.5, any surface of constant is the surface of a sphere of radius (t).

Further reading: For further discussion of cosmology in curved spacetime, see Chapters 6 and 7 of M.V. Berry, 1989, Principles of Gravitation and Cosmology, 2nd edition (Institute of Physics Publishing, London).

According to general relativity, Hubble's law is just one symptom of the expansion of curved space; the distance d between galaxies with fixed comoving coordinates , , expands proportionally to (t). Since d s, Equation 7.5 tells us that the two systems are carried away from each other at a speed

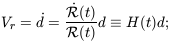
(7.7)

here H(t) is the Hubble parameter, which presently has the value H₀.

Relativity tells us that the distance between two events happening at different times and in different places depends on the motion of the observer. But all observers will measure the same proper time along a path through space and time connecting the events, given by integrating

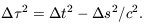
(7.8)

Light rays always travel along paths of zero proper time, = 0. If we place ourselves at the origin of coordinates, then the light we receive from a galaxy at comoving distance _e has followed the radial path

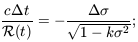
(7.9)

it covers less comoving distance per unit of time as the scale of the Universe grows. We can integrate this equation for a wavecrest that sets off at time t_e, arriving at our position at the present time t₀:

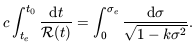
(7.10)

Suppose that _e is the wavelength of the emitted radiation; then the following wavecrest sets off later, by a time t_e = c _e. We receive it with wavelength _obs, at time t = c _obs after the previous crest. But the galaxy's comoving position _e, and the integral on the right of Equation 7.10, have not changed; so the left side also stays constant:

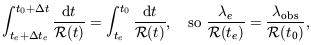
(7.11)

as long as t << (t) / 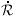(t). The wavelength grows along with the scale length (t), while the frequency, momentum, and energy of each photon decay proportionally to 1 / (t). The measured redshift z of a distant galaxy tells us how much expansion has taken place since the time t_e when its light was emitted. This is the cosmological redshift of Equation 1.28:

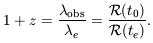
To describe processes in the expanding Universe, we can use redshift as a substitute for time: z(t) is the redshift of light emitted at time t, reaching us now at time t₀. The time corresponding to a given redshift depends on the function (t); once we know this, Equation 7.10 tells us the comoving distance _e from which the light would have started.

The rate at which the Universe expands is set by the gravitational pull of matter and energy within it. We first use Newtonian physics to calculate the expansion, and then discuss how general relativity modifies the result. Consider a small sphere of radius r, at a time t when our homogeneous Universe has density (t); we take r >> (t), so that we can neglect the curvature of space. Everything is symmetric about the origin r = 0, so we appeal to Newton's first theorem in Section 3.1: the gravitational force at radius r is determined only by the mass M (< r) within the sphere. If our sphere is large enough that gas pressure forces are much smaller than the pull of gravity (see Section 7.4 below), then Equation 3.20 gives the force on a gas cloud of mass m at that radius:

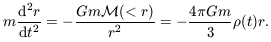
(7.12)

Our sphere of matter is expanding along with the rest of the Universe, so its radius r(t) (t). The mass m of the cloud cancels out, giving

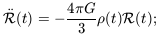
(7.13)

the higher the density, the more strongly gravity slows the expansion.

Nothing enters or leaves our sphere, so the mass within it does not change: (t) ³ (t) is constant. Multiplying by 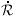(t) tells us how the kinetic energy decreases as the sphere expands:

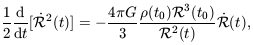
(7.14)

where the time t₀ refers to the present day. Integrating, we have

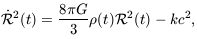
(7.15)

where k is a constant of integration. Although we derived it using Newtonian theory, Equation 7.15 is also correct in general relativity, which tells us that the constant k is the same one as in Equation 7.15. Since the pressure p of a gas contributes to its energy and hence to its gravitational force, general relativity amends Equation 7.13 to read

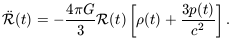
(7.16)

Equation 7.15 and 7.16 describe the Friedmann models, telling us how the contents of the Universe determine its expansion. For cool matter, where the sound speed c_s << c, we have p ~ c_s², and can safely neglect the pressure term. But for radiation, and particles moving almost at the speed of light, pressure is important: p c² / 3, where is now the energy density divided by c². For any mixture of matter and radiation, the term + 3p / c² must be positive, so the expansion always slows down. If the Universe enters a contracting phase, the collapse speeds up as time goes on.

The inflation theory postulates a vacuum energy, contributing density _VAC = / 8 G, and negative pressure or tension p_VAC = - c² / 8 G. The vacuum energy is now very small, but there are reasons to believe that very early, at 10^-34 s t 10^-32 s, _VAC might have been much larger than the density of matter or radiation. During this period, (t) inflated, growing exponentially by a factor ~ e¹⁰⁰. The almost uniform cosmos that we now observe would have resulted from the expansion of a tiny near-homogeneous region. Because this patch was so small, the curvature of space within it would be negligible; hence devotees of inflation expect our present Universe to be nearly flat, with k = 0.

Since (t) ² (t) decreases as (t) grows, in a closed Universe with k = 1 the right side of Equation 7.15 becomes negative at large . But 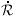² cannot be negative, so the distance between galaxies does not grow forever; (t) attains some maximum before shrinking again. In an open Universe with k 0, there is no such limit; expansion continues indefinitely and (t) grows without bound. In the borderline case k = 0, Equation 7.16 requires that the density is equal to the critical value

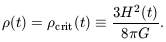
(7.17)

At the present day, the critical density _crit (t₀) = 3.3 x 10¹¹ h² M Mpc^-3: see Equation 1.24. We can measure the mass content of the Universe as a fraction of the critical density, defining the density parameter (t) as

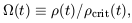
(7.18)

and writing ₀ for its present-day value. Equation 7.15 then becomes

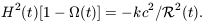
(7.19)

If the Universe is closed, with k = 1, then (t) > 1 and the density always exceeds the critical value, while if k = -1, we always have (t) < 1. If the density is now equal to the critical value, so that ₀ = 1, then (t) = 1 at all times. Most astronomers would agree that 0.05 ₀ 1; our real Universe is unlikely to be much denser than the critical value.

In its early stage, the Universe was radiation dominated. It was extremely hot, and its energy was almost entirely due to radiation and relativistic particles; these are particles moving close to light speed, so that their energy, momentum and pressure are related in the same way as for photons. The energy density _r c² of a gas of photons decreases as ^-4 (t): the number per unit volume is proportional to 1 / ³ (t), while by Equation 7.11 the energy of each photon falls as 1 / (t). As expansion proceeds, the density _m of matter decreases more slowly, since _m (t) ^-3 (t). So at late times, its energy density _m (t) c² exceeds that in radiation. Since the time t_eq of matter-radiation equality, about a million years after the Big Bang, the Universe has been matter dominated.

To measure the expansion of the Universe relative to the present day, we define the dimensionless scale factor a(t) (t) / (t₀). Using Equation 7.19 to rewrite (t₀) in terms of H₀ and ₀, Equation 7.15 becomes

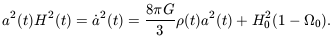
(7.20)

Most of the structure of galaxy clusters and voids that we see today developed after the Universe became matter dominated. In this phase, the density falls as a^-3, and from Equation 1.28, 1 + z = 1 / a(t); so Equation 7.20 reads

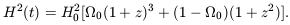
(7.21)

If the density is exactly at the critical value, with ₀ = 1 and k = 0, we have a^1/2, and a(t) t^2/3.

Since the Universe is not completely empty, ₀ > 0. Hence the first term on the right of Equation 7.21 will be large when a(t) is small, soon after the Big Bang; we again have a(t) t^2/3. Thus as t -> 0 in the early Universe, space is nearly flat and -> 1. If the density is below critical, with (t) < 1, then at late times the second term of Equation 7.21 takes over, giving a(t) t. Expansion then proceeds almost at a constant speed, barely slowed by the gravity of matter. Using the redshift z to specify time indirectly, in a matter-dominated Universe we can write

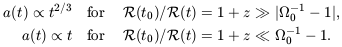
(7.22)

We believe that ₀ 0.05; so the Universe expanded with a(t) t^2/3 from the time of matter-radiation equality until at least z ~ 18.

Problem 7.12: Even if the cosmos has infinite volume, we can observe only a finite portion. From Equation 7.10, light reaching us at = 0 by time t originates within our horizon at comoving radius H, defined by   (7.23) At early times the Universe was radiation dominated, with (t) t1/2, and we can disregard the curvature k; show that then, (t) H = 2 c t. Explain why only points within this distance can exchange signals or particles before time t. (At the time of matter-radiation equality, a patch of diameter H (teq) would subtend about 3° on the sky. By the present, this region has expanded to ~ 13 (0 h2)-1 Mpc, and contains a mass MH 1015 (0 h2)-2 M in neutrons and protons. Little time elapsed between teq and recombination, when the matter became neutral, and photons of the cosmic background radiation could stream freely toward us. So it is somewhat surprising that the cosmic microwave background has almost the same spectrum across the whole sky. Inflation theory would allow large-scale uniformity to be established before expansion began to proceed according to Equation 7.20.)