


2.1 Morphological Classification of Collisional Forms
The short answer to the question above is - a tremendous variety of forms. This is perhaps the place for the reader to put down this article and peruse the Arp or Arp-Madore atlas for an hour or so, if he/she has not done so before! These galaxies would not have been tossed into the "peculiars" bin if they could have been fitted into simple scheme like the Hubble classification. On the other hand, the instinct to classify and order is strong, and all of the major collectors of images of these systems - Zwicky, Verontsov-Velyaminov, Arp, Madore - developed some phenomenological system. For example, Arp (1966) arranged his 338 atlas galaxies into 37 descriptive catagories. Arp and Madore (1987) used 24 similar, but simplified catagories. Vorontsov-Velyaminov (1977) has a longer list of descripters. Many of the terms used in these atlases, along with a number of other anecdotal descriptions, are now used commonly, but in no uniform way.
Schweizer (1990) has proposed a simple, elegant alternative. If the Hubble sequence from early-type ellipticals to late-type spirals is like a continuum line, then Schweizer's classification of collisional galaxies consists of the plane of Cartesian pairs of progenitor galaxies. Basically, he uses a simplified Hubble sequence of three types: ellipticals E, disk galaxies D, and gas-rich irregulars G. Given the difficulty in determining the detailed nature of the progenitors in many cases, this simplification seems imminently justified. Schweizer also adopts a clever device - upper case letters to indicate the large or primary galaxies in the system (e.g. DD to indicate a collision between two comparably sized disk galaxies), and lower case letter to indicate small companions (e.g. Ed for a collision between a small disk and a large elliptical).
Empiricists could object that this scheme is not a direct classification based only on features that are seen in the (optical) image of the galaxy. It requires an inference as to the type of the progenitors. Moreover, it assumes that the progenitors had a definite Hubble type, and that the distortions are mostly the result of the collision. However, the weight of the evidence overwhelmingly favors this assumption in most cases. In addition, in many cases the classification doesn't depend as much on interpretation as on the use of other types of data, such as 21 cm observations of gas content, or kinematical data to detect a disk component.
The advantage of the earlier descriptive systems is that they highlight the transient morphologies of the ongoing collision, whereas there are many morphologies within each category of Schweizer's scheme. Some of these morphologies are very short-lived, and others long-lived (see below), so (relative) lifetimes are also a natural parameter for classification. In a study of color trends among tidal features in interacting systems Schombert et al. (1990) used a very simple scheme (bridges, tails, mergers) based on this idea. Schweizer and Seitzer (1992, 1992) have developed a semiquantitative system to measure tidal features in isolated (but presumably merged) ellipticals and S0 galaxies. Other classification systems have been developed for specific purposes, but these examples illustrate both the difficulty of developing an all encompassing system, and the utility of specialized systems.
Nonetheless, should it not be possible to give a relatively complete physical characterization (including the nature of the progenitors and the collision parameters) of any collisional system by comparison to computer simulations? In principle this may be true, though there are many practical difficulties. Uniqueness theorems apply to the relevant stellar and gas dynamical equations, if the initial conditions are given with infinite accuracy. In practice, uniqueness at practical particle, spatial and velocity resolutions remains unproven, except in a few specific applications. Moreover, the theorem does not apply to two-dimensional projections (onto the sky) of three-dimensional results. In many cases this point is a mere academic quibble - there is no difficulty in distinguishing an Arp-Madore "Sacred Mushroom" type collisional ring galaxy from a well-developed merger remnant in either observations or simulations. However, less extreme cases are not so clear (see below). The question of uniqueness is also evolving as resolution increases in both observational and modeling realms.
However, even assuming that collisional forms are unique functions of progenitor orbital and structural parameters, their great multiplicity is a problem. Consider this multiplicity from a "first principles" viewpoint. The orbital parameters include a couple of angles of attack specifying the approach direction, and an impact parameter specifying the closest approach of the two centers. The amplitude of the collisional effects depends on the mass ratio of the two galaxies. Absolute timescales for the evolution of these effects depend on actual masses, but the actual values are not important to identifying morphologies, so we only need include the mass ratio among our parameters for the present. Most collisions are relatively quick and impulsive, but the magnitude of the effects does depend on the relative velocity at closest approach (see e.g. Binney and Tremaine 1987, sec. 7.2, henceforth BT). Finally, the orientation of the spin axis of each galaxy disk, relative to the axis of the relative orbit, also effects the outcome. This introduces a bare minimum of one more parameter, assuming only one galaxy has a disk. (Two orientation angles would obviously be better, but the primary effects depend on whether the orbit is prograde or retrograde relative to the disk spin.) Thus, we have a total of 6 or more orbital parameters.
Next we must consider structural parameters. The most important of these are the mass ratios of different components, e.g. bulge/disk/stellar bar/halo. The gas fraction in the disk is also important. The scale length of the various components, or relative compactness, is another important parameter. There are many other structural parameters, e.g. the velocity dispersions (or temperatures) of the various components, or their density profiles. Velocity dispersion is probably not independent of the other parameters, in fact, masses and scale lengths may not be independent. Moreover, the density profiles may be sufficiently universal that they can be omitted as a parameter. Nonetheless, we have a minimum of about 7 structural parameters.
We see that, if we consider a minimal grid of models, with say, 10 values for each parameter, we would need of order 1013 computational runs. Then, of course, time is a crucial parameter. Simulations generally show great temporal variations over the course of e.g. a Gyr. run, so we would probably want to look at 30 or more snapshots to represent the whole evolution. More if we want to see more than one orthogonal view at each timestep. This is beginning to make for a very large family photo album! We have also been assuming that collisions only involve two galaxies at a time, but encounters involving three or more galaxies are probably not uncommon in groups and clusters (see chapters 1, 9). Consideration of three body collisions would clearly enormously increase the number of runs needed for a complete catalog. It seems that direct physical classification by reference to a complete numerical atlas with adequate resolutions is not the way to go. There are too many possible computer realizations to assemble a complete atlas of all collisional systems.
This result has a number of nasty corollaries, including - the perfect computer match to a given system may be lost in an unexplored part of phase space. This can be true even if you've already found a "perfect" match, because uniqueness isn't guaranteed at any given level of resolution. Another interesting corollary - a hypothetical computer atlas like that described above would contain far more snapshots of collisional galaxies than will be observed on the sky within the foreseeable future. In fact, since there are of order 0.01 average galaxies per cubic megaparsec, and the volume of the observable universe is of order 1011 Mpc3, it would contain orders of magnitude more images than there are galaxies in the universe. All the more so since not all galaxies are interacting, and we only get one viewing angle of each system.
These realities certainly influence the choice of problems studied, and the progress made on these problems. For example, the multiplicity and uniqueness appear to significantly complicate studies of collisional shell galaxies, where observation-simulation comparisons are an intrinsic part of the research (see sec. 4.3). They did not have much of a role in early simulations of mergers (see sec. 4.4), where the basic questions of how long does merging take, and what is the approximate structure of the remnant, did not depend on many details. Now that this research has advanced to a much higher level of detail (see Hernquist 1993, Barnes 1998), they may be becoming important.
Nonetheless, the use of distinctive landmark morphologies and common sense rules make it possible to divide up the parameter space into more tractible regions. This judgement seems to be confirmed in the work of Howard et al. (1993), who actually assembled a quite extensive atlas of N-body simulations with 86 runs and 1700 snapshots. (Even so, they had to incorporate several substantial simplifications, including a rigid, inert gravitational potential for the companion galaxy and the halo of the primary galaxy, a two dimensional disk, i.e., not including warps and distortions, and an extremely approximate treatment of gas dynamics in the disk.) Howard et al. discussed a number of generalizations and rules of thumb derived from these simulations, especially with regard to prograde versus retrograde and direct (perpendicular) collisions. Other extensive simulation projects have been carried out and will be discussed below.
Some very useful insights into the role of the collision parameters (and into the uniqueness problem) are provided by Gerber and Lamb's (1994) work. This paper was primarily a comparison of semi-analytic kinematic models to fully self-consistent simulations, in the restricted setting of collisions between a small companion approaching on an orbit nearly perpendicular to the primary disk, though with a range of impact parameters. Gerber and Lamb pointed out that the perturbation in the kinematic models (which were found to match the simulations well at early times), depended on four dimensionless parameters. The first of these is just the time scaling. Another two are the dimensionless impact parameter, and a dimensionless measure of the compactness of the companion. Finally, there is a strength parameter equal to 2GM2 / (bVvc), where M2 is the mass of the companion, b is the impact parameter, V is the relative velocity at impact, and vc is the circular velocity in the primary disk (assuming a flat rotation curve, i.e. vc = constant). This parameter is the velocity disturbance derived from the Impulse Approximation (see Binney and Tremaine 1987, section 7.2 and references therein), divided by the disk orbital velocity, which is proportional to the escape velocity. Because it was derived for a restricted application, this set of dimensionless parameters is incomplete, and also some assumptions about the structure of the two galaxies are embedded in the parameters. However, it is a very good example of how to attack a limited part of the problem.
I will conclude this section with an attempt at a classification scheme that tries to pull together some of the insights from the older morphological systems as well as those derived from analytic and simulation studies of the effects of varying collision parameters. The specific motivation for attempting this here is to provide simple categories, which highlight the relationships between and the natural ordering of the many individual cases discussed in the rest of this article. The system is essentially a modification of Schweizer's system, with the addition of a few variables that are directly related to both the physical quantities characterizing the collision and to observable characteristics.
Because there are a number of collisional forms that are easily identifiable as either short-lived or old, the first variable is time. The actual development timescale of collisional features depends on the masses of the galaxies, and galaxy masses can range over at least 6 orders of magnitude. Thus, the presence or absence of specific features can only yield relative timescales. Age determinations of collision-induced stellar populations might be more accurate in some cases, especially when a single short starburst dominates. (However, in many cases the enhanced star formation may be of long duration, or there may be multiple bursts.) But whatever dating technique is used, for present purposes we limit this variable to three values: young, intermediate, and old (Y, I, O).
In collisions the dynamically cold disks respond the most strongly and the most quickly to the disturbance, so the relative mass of the disk component is significant as a first gauge of the magnitude of the collisional effects. If there is a substantial disk, the gas fraction in the disk is also important. The dynamically cool/hot component ratio and the gas fraction are related, and related to other quantities (as in the Hubble sequence), so it suffices to adopt Schweizer's Hubble pairs scheme. However, I would prefer to modify his definition of category D to include only early-type disks (S0-Sb), and of category G to cover all the later Hubble types. (There is increasing evidence that most gas-rich galaxies have a rotating disk, and are not irregular, see e.g., the recent review of Skillman (1996) on dwarf irregulars.)
I propose only two variables to describe the collision itself, one for
the magnitude and one for the directionality. For the former we can use
Gerber and Lamb's dimensionless strength parameter. As defined, this
parameter is not an observable, but it can be brought closer to observables
with some additional assumptions, which are valid for the most common cases.
Most collisions probably involve members of bound galaxy groups. If the mass
of the collisional system is dominated by a dark matter halo encompassing the
whole group, or by the halo of the primary galaxy (e.g. a small companion), it
is reasonable to assume that V  vc (relative impact velocity approximately equals
circular velocity in primary disk). Then using the equation of centrifugal
balance in the disk, we can substitute G/vc2
vc (relative impact velocity approximately equals
circular velocity in primary disk). Then using the equation of centrifugal
balance in the disk, we can substitute G/vc2
 R/M1, where
M1 (= M1(R)) and R are the mass and
disk radius of the primary. Then the strength parameter becomes,
R/M1, where
M1 (= M1(R)) and R are the mass and
disk radius of the primary. Then the strength parameter becomes,
The ratio b/R is still not an observable, but in most collisions with
significant effects, its value ranges from a bit less than unity up to of
order a few. (In head-on collisions b is replaced with an effective
"softening" length.) Thus, S is roughly equal to a factor of order
unity times the mass ratio M2 / M1, so at a coarse
level of description we can use the two
interchangably. Note: these approximations are not valid for high-velocity
collisions, such as occur in large galaxy clusters.
In this article a qualitative estimate of S, or just an indication of
whether it is small, medium or large will suffice. In the latter class are
collisions between nearly equal mass galaxies. We can define the
"small" class as consisting of collisions with companions of such
low mass that the companion is likely to be disrupted or stripped of
substantial mass, e.g. S < 0.1. (Of course, this consequence is determined
by more than just the mass ratio, a complication we accept as part of the grey
area between qualitative classes.) We again adopt a modified form of
Schweizer's notation, using upper case letters in the Hubble variable for the
primary galaxy and comparable companions, lower case for medium strength
companion interactions, and subscripts for low strength
encounters. Thus, Ed represents a disruptive collision between an
elliptical and a small disk.
The last classification variable is for directionality or angular
momentum coupling. For each disk component involved we assign a value of +,
0, or -, depending on whether the encounter is prograde, perpendicular (or
head-on), or retrograde, relative to the spin of that disk. Thus, a recent
planar encounter between two comparable disk galaxies, at an early stage might
have a classification of YDD+- (or YDD++ or YDD--). A variable of unknown
value will either be omitted, or highlighted with an x (e.g., YDDxx). Another
example, an elliptical shell galaxy would be OE; a model of this galaxy might
be OEd+. In the remainder of this article,
where appropriate, the collision categories described in each section will be
given in parenthesis in the section title. The classification variables and
the range of values considered are summarized in
Table 1.
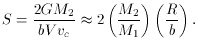
Timescale Y (young) I (intermediate) O (old)
 108 yr
108 yr
108-108 > 109
Hubble Type for each galaxy
E
D
G
(Disk component,
elliptical, spheroidal
significant disk
gas disk, or irregular
gas fraction)
Companion Mass,
Small < 10%
Intermediate  10-50%
10-50%
Large > 50%
perturbation Amplitude
denote by subscript
lower case
upper case
Spin-Orbit
+
0
-
coupling
Prograde
Orthogonal
Retrograde
(for each galaxy)