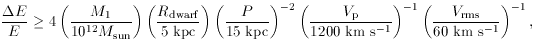4.1. Transient Mass Transfer and Bridges
Most collisions or near misses involve some exchange of material between galaxies. Under specific circumstances described below the amount of material exchanged can be considerable. In this subsection we will consider cases where the collision does not end in a prompt merger, and does not result in the large-scale disruption of the partners. Even in these cases the mass transfer can significantly influence the evolution of both galaxies. There are two general reasons for this. 1) A large fraction of the material transferred is usually ISG (interstellar gas), the seminal material of galaxy evolution. 2) The transfer, and the forces that drive it, upset the thermo-hydrodynamical (quasi-)equilibrium of the gas disks, initiating a long-term relaxation process. These points apply not only to mass exchanges between galaxies, but also to the case of mass forced out of galaxy disks into large tidal structures, such as bridges and tails. In both cases material falls onto the galaxy disks on an extended timescale. Transient mass transfer can also be viewed as a large scale experiment in ISG dynamics, and thus, can be used to further our understanding of these processes.
There are basically two modes of mass transfer in these situations: hydrodynamic and tidal. By the former, I mean the case of a direct collision between the gas disks of the two galaxies. (In this category we also include the collision of the hot gas halo components, but this is generally of minor importance for the two galaxies, see section 1.) In the second mode material is pulled out of at least one galaxy by gravitational forces. Specifically, this mode usually works by increasing angular momentum via tidal torques, rather than by direct gravitational attraction. Thus, it is the dynamically cold, spinning disk material that is most vulnerable to the exchange process. The resulting tidal features often have a large gas fraction because the neutral hydrogen disks of most galaxies are larger than the stellar disk, and the outer parts are more loosely bound. We will consider each of these modes separately.
4.1.1. Splashes: Bridges and Infall in Direct Collisions (YDd0)
As discussed in section 1, when two gas disks collide, the diffuse gas clouds within them will collide at highly supersonic speeds. Thus, we can expect an extensive gas splash, and the observable effects of shock heating and radiative cooling. We do not have to look far for examples of supersonic collisions involving external clouds. Our Milky Way galaxy contains a population of so-called High Velocity Clouds (HVCs), which unlike other interstellar clouds, are not confined to the disk, and which have very different kinematics. In recent years several studies have provided good evidence for recent or ongoing collisions between some HVCs and disk clouds (e.g., Cabrera-Cano et al. 1995, Tamahana 1995), possibly including the nearby Gould's Belt region in Orion (Comeron & Torra 1994). In addition, Mirabel & Morras (1990 and references therein) have argued that a stream of clouds is impacting the disk in the anticenter direction. These impacts are usually discovered in observations of the flux and distribution of the radio continuum emission from hot gas, and the distribution and kinematics of the (infalling) neutral hydrogen gas.
The galactic disk HVC collisions may also be an example of mass transfer induced by a galaxy collision. Mirabel & Morras' stream may be connected or related to the Magellanic stream, a partial ring of HI gas around the galaxy, and connected to the Magellanic Clouds (and the bridge between them). Recent models support the old conjecture that the Magellanic stream may be a bridge-tail structure resulting from the interaction between the Magellanic Clouds and the Galaxy (e.g., Lin, Jones, & Klemola 1995, and references therein). Stunning new maps of the HI gas in these structures have recently been presented (Stavely-Smith et al. 1998 and in progress), and constraints from these data should allow the construction of much more detailed models in the near future.
Hydrodynamic mass transfer in many colliding galaxies involves cloud collisions on a much larger scale than the HVC-disk interactions in the Milky Way. (Despite the fact that the latter involve regions of size greater than 1.0 kpc.) Bridges or plumes in these systems have gas masses comparable to or greater than the Magellanic stream. Let us consider a few specific examples from the recent research literature.
HI observations have also provided kinematic evidence for a cloud-disk collision in the nearby galaxy M101 (van der Hulst & Sancisi 1988). According to Kamphuis (1993, and see van der Hulst 1996) the kinematically disturbed region "is over 20 kpc in size and contains a few 108 solar masses of HI and reaches velocities up to 160 km/s above the local rotation." This is certainly the most impressive example of the phenomenon among the nearby galaxies.
Another very appropriate example is the system UGC 12914 / 5, called the "Taffy" galaxies by Condon et al. (1993). (The term was also used by Zwicky in 1956 for such "sticky" systems, according to TT.) These authors note that "almost half of the (radio continuum) flux... arises from the gap between UGC 12914 and 12915, across which radio contours are drawn like filaments of Taffy." Besides radio continuum emission, and the magnetic fields and cosmic rays assumed to produce it, there is also abundant HI gas in the bridge connecting the two galaxies. From the spatial distribution of these emissions, and the continuous kinematics along the bridge, the authors conclude that this is, in fact, the splash following the "interpenetration" of two galaxy disks. Interestingly, there is little recent or ongoing star formation in the bridge. It is also interesting that one of the two galaxies is a ring galaxy.
Thus, the Taffy system is probably a close relative of galaxies in the "Sacred Mushroom" class of Arp and Madore (1987). (Even if the culinary association does not sound promising!) A Sacred Mushroom is defined by a stem consisting of an edge-on or disrupted companion connected to a ring galaxy cap. The fact that the two galaxies are still in contact (at least in projection) implies that the collision is not quite over. The companion orientation is different in the Taffy system, but the collision may not be any older. The prototype Sacred Mushroom is the AM 1724-622 system (see Fig. 1). Unfortunately, the primary in this system was apparently gas poor, and thus, it is not a good splash example (see Wallin & Struck-Marcell 1994).
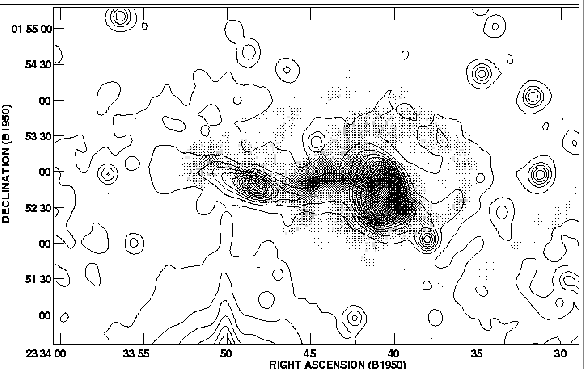
Arp 284 (NGC 7714/5) provides a better example, according to the HI observations and modeling of Smith and Wallin (1992), even though it has a rather small cap-to-stem ratio, see Figure 13. This system is especially interesting because the Smith & Wallin model suggests that the bridge may be the result of the combined action of gravitational and hydrodynamic procesess. The recent high-resolution HI observations (see Smith, Struck and Pogge 1997) show that the bridge gas and HII regions are both spatially offset from the stellar bridge by a large amount, which, along with new hydrodynamic models, provides support the notion that they are the result of different physical processes. The large amount of HI gas in this bridge also shows how effective these processes can be.
|
Figure 13. The bridge connecting the two galaxies of the Arp 284 system. A VLA multi-array intensity map of the HI gas (grayscale) is superposed on a narrowband red continuum image (contours) smoothed to 12 arcsec resolution (see Smith et al. 1997 for details). The offset in the bridge between the gas (dark ridge) and the old red stars is about 10 arcsec. |
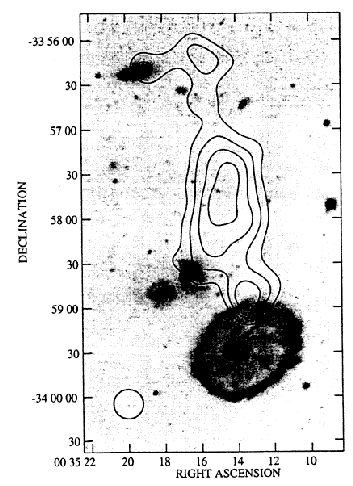
Recent HI observations have revealed long HI bridges or plumes in two classic ring galaxies indicating that they are at least closely related to the "Mushroom" class. The Cartwheel ring appears to have a fully connecting bridge (see Fig. 14 from Higdon 1996), while the plume of the ring galaxy in the VII Zw 466 system is not so complete (Appleton, Charmandaris, and Struck 1996). In both cases the long bridges have thus far only been seen in neutral hydrogen emission.
|
Figure 14. The HI gas bridge in the Cartwheel system from Higdon (1996). |
Like the Taffy system, all of these other systems show little or no new star formation, with the exception of Arp 284, the transition system involving both tidal and hydrodynamic mass transfer. It is not surprising that splashes inhibit star formation since they disrupt disk clouds, and lead to an overall rarefaction of disk gas. As we will discuss below, our understanding of the physics of large-scale star formation is very incomplete. It seems clear that compression is a key, though it may only be the initiator of a multi-step process. On the other hand, direct triggering of star formation in high velocity cloud-cloud collisions is another popular idea that is very relevant here. This is emphasized by the fact that the Milky Way HVC galactic disk collisions seem to have triggered star formation (e.g., Cabrera-Cano et al. 1995, Comeron & Torra 1994). Nonetheless, this induced star formation seems to be very modest compared to that triggered in large-scale compression waves.
4.1.2. Models and Splash Physics
Probably the first authors to describe the gas dynamics of collisions between two galaxy disks were Spitzer and Baade (1951, see section 1.3). However, this paper was not followed up by many observational studies until the recent examples above, in part because the detector technology wasn't adequate (but see Fabbiano & Trinchieri 1983). Spitzer and Baade were decades ahead of their time.
Because of the nonlinear, dissipative shock hydrodynamics, and the wide range of scales involved, it is also a difficult process to simulate numerically, so theoretical progress was impeded too. There is a fairly extensive literature on supersonic collisions between interstellar clouds, and between clouds and large-scale shocks, dating from the early 1970s. This work provided a basis for the simulations of Tenorio-Tagle (1981, and Tenorio-Tagle et al. 1986, 1987) on collisions between HVCs and the galactic disk. In this series of papers it was demonstrated that such collisions had enough energy and momentum to generate the largest loops or supershells of HI seen in our galaxy. These models also demonstrated, that depending on the density and velocity of the impacting clouds, they could either dump most of their infall energy in the galactic disk, or punch a cylindrical hole in the disk and retain part of their energy. It is possible that such holes and other manifestations of cloud infall out of a bridge have been observed in recent HST observations of the Cartwheel ring galaxy (Struck et al. 1996). However, the high-resolution observations were only made in two broad bands (B and I), so shock emission could not be distinguished from other sources.
In 1987, Harwit et al. presented a paper that can be regarded as an update of Spitzer and Baade, detailing the infrared emission expected in disk-disk collisions. This paper was inspired by then new IRAS discoveries of ultraluminous galaxies, and suggested that some might be the results of such collisions. The subsequent realization that many of the ultraluminous galaxies were probably merger remnants, led many researchers to persue studies of the spectacular merger dynamics, where gas splashes play a secondary role (see below). Recent merger simulations do include the gas component in the disks of both galaxies (see section 6), but the discussion focusses on the final gas distribution in the merger remnant, rather than the transient splash dynamics.
However, the recent paper of Thakar and Ryden (1996) does discuss gaseous infall onto disks, and the formation of counter-rotating disks (discussed below). This paper highlights the role of infall or collisions with dwarf companions in dynamically heating galaxy disks, thus demonstrating one long-term evolutionary effect.
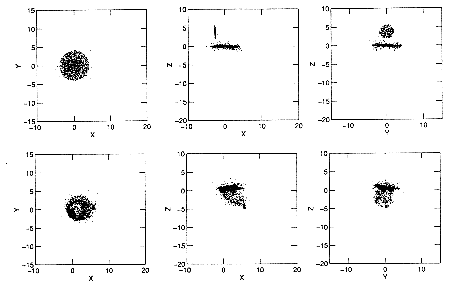
A small grid of Smoothed Particle Hydrodynamics simulations carried out by the author are complementary to those of Thakur and Ryden, in that direct collisions with an intermediate mass companion (about a 1:3 mass ratio) were studied (Appleton, Charmandaris, & Struck 1996, Struck 1996, 1997). One of the main motivations for these simulations was to model the HI bridges in the ring galaxies VII Zw 466 and the Cartwheel, which are very gas rich, so the model disks were purely gaseous (and were embedded in a rigid halo potential). Cooling and heating processes were also included. The orbital trajectories were such that following the collision the companion continued outward to a distance of several primary disk diameters, before falling back for a second collision. Not surprisingly, the initial impact did indeed produce a substantial splash, which was then stretched out into a long bridge between the two galaxies (Fig. 15). Because of the size difference much of the primary disk remained intact following the collision, but in all cases the companion was highly disrupted. In some cases it was nearly completely disrupted.
|
Figure 15. Three orthogonal views at two times, immediately before and after the collision of two gas-rich, disk galaxies in a numerical hydrodynamical simulation. As in observed systems the collisional splash produces a substantial gas bridge, while leaving the primary disk largely intact. See Struck (1997) for details. |
After an initial delay, in which most of the bridge gas stretches away from both galaxies, infall onto both galaxies accelerates. This (re)accretion generally occurs out of distinct streams within the bridge gas. The accretion rate peaks and then declines before the two galaxies fall back together. In all cases the companion reaccretes less gas than it had initially, though the recaptured gas generally forms a smaller, more compact disk, a likely site of later star formation. The gas mass in the bridge, and its galaxy of origin, are found to depend sensitively on the orientation of the companion disk at the time of impact. The bridge can consist mostly of gas from the primary disk (face-on impact), gas from the companion (companion disk in its orbital plane), or a nearly equal mixture of both.
The ramifications for the short-term evolution of the companion are extreme. E.g., partial to complete removal of its gas disk, and reformation with a very different structure and composition. These, and analogous transfigurations of stellar bulge and dark halo components (not modeled in these simulations), will have important effect on subsequent collisions and merger. This is also true of changes in the primary, though they are less extreme. The accretion onto the primary is only of order 10% of its gas mass, but the infalling material has relatively low angular momentum, so it tends to concentrate in the central regions. Infall heats gas in the central regions. Thus, it initially inhibits star formation there, according to the algorithm used in these simulations, which requires dense, cool-to-warm gas for star formation (henceforth SF). Moreover, the accreted gas initially settles into a second inner disk, with a significantly different orientation than the primary disk, like the "counter-rotating" disks of Thakar and Ryden. However, as this gas settles in it provides a reservoir to fuel (delayed) starbursts and nuclear activity. The timing of this activity relative to the return time of the companion will determine how much gas is available during the final merger, which in turn influences the final structure of the remnant.
A small, but important, coda to this story - most published galaxy collision simulations, which include a gas component, employ an isothermal equation of state. This approximation is based on the fact that free cooling times in the interstellar gas are very short compared to other relevant timescales in galactic dynamics. Yet, this neglects the fact that in star-forming regions, stellar winds, high UV photon fluxes, and supernova explosions provide continuing sources of heat, and so the local thermal balance is probably dynamical. In the Struck (1996, 1997) simulations comparisons were run between isothermal and cooling/heating models. Most of the large-scale tidal morphologies and wave structures are very similar. There are small differences that could be attributed in some cases to the different jump conditions in the impact shock (i.e., isothermal vs. locally adiabatic). However, there are also larger differences, like the fact that star formation cannot occur in some regions with high gas density, because the region was heated by infall or previous star formation. The treatment of thermal effects and even the resolution of cloud structures is highly approximate in present-day simulations, but there are clearly many interesting effects to study as the state of the art advances.
4.1.3. Slings: Tidally Torqued Bridges (YDx+)
Bridge formation and mass transfer in the tidal process affects stars and gas more equally, and has been studied longer and in more detail than the splash process. In fact, the tidal stretching and spin-up that generates a mass transfer bridge is the same process that makes the tidal spirals discussed above. Thus, the first models of tidal bridges were in fact the earliest interaction models. The process is clearly illustrated in the papers of the Toomres (1972) and Eneev et al. (1973). The former contains the first systematic investigation of the process, and presents the basic laws governing it. The first and most important is that the most mass transfer from the primary to the companion occurs when the encounter is in the plane of the primary disk, and prograde relative to it. More generally, TT concluded that collisions with inclinations of less than 30° produced "real" (mass transfer) bridges, and those with inclinations of more than 60° did not. Wallin and Stuart 1992 (henceforth WS) carried out a huge grid of restricted three-body simulations to model tidal mass transfer as a function of interaction parameter. Their Fig. 5 confirms the TT result, and shows quantitatively the rapid decrease of transferred mass in the intermediate inclination range. Retrograde encounters do produce tidal tails, but they either form too late, or on the wrong side of the galaxy to connect with the companion near closest approach. Similarly, high inclination companions have generally moved too far from the primary disk plane by the time tails, which are potential bridges, form.
Thus, qualitatively, the criterion for mass transfer is that the companion must orbit roughly along with particles in the primary for a significant fraction of their orbit. This not only provides time for bridge formation, but allows enhanced gravitational torques from the companion to propel the particles outward.
Another law of bridge formation from TT is that the bridges (and tails) are not three dimensional objects. They tend to form on two dimensional surfaces, which look like a continuously deformed or tilted version of their original orbital plane. From the considerations of the previous paragraph it is reasonable to suppose that the accelerations in the direction perpendicular to this plane will be relatively small, unless the perturbed particle is very close to the companion (or is swung above or below it).
For encounters with a fixed inclination, the amount of mass torn from the primary disk also depends sensitively on the mass ratio of the two galaxies, and the closest approach distance. These dependences were studied by WS in the case of parabolic encounters on zero inclination orbits. If the companion mass is less than the primary, and its closest approach distance is more than twice the outer radius of the primary disk, then WS found that the primary will lose less than 5% of its disk mass. If the closest approach distance equals the primary disk radius, then it was found that up to about 40% of the primary disk mass is removed.
In such extreme cases the restricted three-body approximation is almost certainly inaccurate, and so too the derived mass loss rates. Both disk self-gravity and distortions of bulge and halo components, among other effects, are probably important. However, as long as the encounter is rapid and impulsive, these factors may affect the amount of mass removed less than they affect where it ends up. These variables will also be determined by the structure and extent of the primary halo. With a scale length of 1-2 disk radii, the halos used by WS were of moderate extent. They found that typically about half of the (stellar) particles removed from the primary became bound to the companion, with the remainder becoming unbound to either galaxy. With dissipative gas one would expect a smaller fraction to escape.
The figures in WS seem to suggest that some relatively simple scaling
relationships might exist for the mass loss as a function of the various
parameters. Having such relations would facilitate the comparison of their
results to more detailed, self-consistent simulations, and perhaps, to
observation. (Though determining interaction parameters, let alone the amount
of mass transfer, from observation is an extremely difficult undertaking.)
The simplest scalings can be derived from the KIA formalism described above,
with the additional assumption that the impulsive acceleration is imparted
while the companion travels over a small angular sector

 of its orbit near closest approach.
of its orbit near closest approach.
For the parabolic companion orbits usually considered, this sector can
be approximated by a circular arc centered on the primary. Moreover, the
relative velocity of the companion will not vary much in the time interval
 t during which the segment is
traversed. This
velocity will approximately equal the escape velocity from the primary at the
companion radius,
t during which the segment is
traversed. This
velocity will approximately equal the escape velocity from the primary at the
companion radius,
If rcomp is in the range 1.0-2.0 disk radii,
then this is also about equal to the circular velocity of disk particles
located just inside the outer radius. The conclusion is that the disk
particles in the sector
where we apply this to primary disk particles following the companion.
Particles which lead the companion around the primary disk will have their
angular momentum reduced by the azimuthal impulse. They will then fall inward
unless the radial impulse is larger (see sec. 3.4).
To estimate the mass loss let us assume that particles with impulses
greater than
will be lost. Without calculating the overlap area of this circle and the
disk, we can assume that it, and the mass loss scale as
Despite the many simplifications, this scaling seems to capture several
of the WS results. First of all, with other parameters fixed, both this
formula and the simulations agree that mass loss scales nearly linearly with
companion mass. Secondly, the angle
However, the third dependence, on the closest approach distance, is not
clarified by the formula above. If the WS results are approximated by a power
law, i.e., mass loss scales as 1/rn, it appears
that n
In summary, significant tidal mass transfer only occurs when the
companion orbit inclination is less than about 45°, and the closest
approach distance is less than about 2.0 primary disk radii. Hydrodynamic
splashes can occur in collisions with any inclination, but the distance of
closest approach must be less than the sum of the disk radii. The dependences
of mass loss on the companion mass may not be too different in the two cases.
Thus, since the first two factors are offsetting, the relative importance of
the two processes for net mass transfer between galaxies may be about equal.
This is somewhat surprising because systems with companions that appear to be
connected by tidal bridges are very common in the peculiar galaxies atlases
(e.g., "companions on arms" in Arp 1966, M51 types in
Arp and Madore 1987).
Obvious splash systems are not so common. However, there are a couple
of straightforward explanations. The first is that the cross sections and
impact parameters for generating tidal arms or tails are much larger than
those for mass transfer, and the probability for apparent superpositions of
arms and companions is not small. The second is that ongoing star formation
is frequently lights up tidal tails, while splashes are usually invisible
optically.
4.1.4. Observations of Tidal Bridges and Star
Formation
M51, the "Whirlpool" galaxy, is the most
conspicuous example
of a galaxy with a companion on the end of an arm (see
Fig. 10).
Unfortunately, TT argued that the connection is in fact only apparent, and not
a physical connection. They found that their models could not reproduce the
detailed arm morphology and other tidal features in the brief time the two
galaxies were connected. Also reddening observations suggest that the arm
lies in front of the companion. Later, fully self-consistent simulations
agree that it is difficult to produce the observed morphology during a brief
parabolic passage (e.g.,
Hernquist 1990).
Howard and Byrd (1990)
suggested
that the companion is on a bound orbit, and that two disk crossings account
for the observations best. A review of the recent models, and a more detailed
version of the two-crossing model is presented in
Byrd and Salo (1995).
In any case, it appears that under close scrutiny M51 has become too
complicated to be a true prototype for the simplest forms of transient
tidal mass transfer.
Laurikainen, Salo, and Aparicio
(1993 and
Salo & Laurikainen
1993)
have recently presented detailed studies of another M51-type system, Arp 86,
which may be simpler. In the Arp atlas it appears very simple compared to its
atlas neighbor Arp 85 = M51. Salo & Laurikainen carried out a set of
detailed N-body, star-gas simulations of this system, and found a
best-fit
model that fits both the observed morphology and kinematics remarkably well.
In this model the companion mass is about 10% of the primary, and it has a low
inclination orbit, i = 20°. However, it is a bound, low eccentricity
(quite circular) orbit. Salo & Laurikainen find that the disturbed
morphology is well accounted for as the result of the tidal disturbances on
the last half-orbit, but this involves two close passages, with the earlier
one playing the larger role in generating the present features. Deja vu M51.
Salo & Laurikainen also found an interesting result by running
their simulation far into the future of this system, i.e., through three more
companion orbits. The model shows that the companion is connected to the
primary for a considerable fraction of this time, though at late times the
bridges have a very messy appearence. The authors make the reasonable
conjecture that the original orbit was parabolic, but that dynamical friction
(see below) led to capture and circularization of the orbit. Given the
relative durations of the initial encounter versus the sum of later encounters
it seems likely that this is true of many M51-type systems, and that the
catalog objects are probably distributed along a generic sequence of transient
encounters, rather than being primarily first encounter objects.
Some record of this sequence of events might be found in the stellar
populations of these systems, if the perturbations produced at closest
approach generate transient episodes of enhanced star formation. A great many
numerical models of prograde, low inclination interactions have been produced
over the last few decades, and they all agree that there is enhanced
compression in the tidally induced arms, tails and bridges, which probably
drives enhanced SF. In fact, there is a good deal of observational evidence
for ongoing, and enhanced, SF in tidal bridges (and tails).
Schombert et al. (1990)
presented photometric imaging of tidal features in 25 Arp systems.
They found relatively blue mean colors and large color dispersions indicative
of ongoing SF in many of these features, and especially in the
bridges. The H
Nonetheless, this result is in sharp contrast to the splash bridges,
which evidently expand and disperse gas, and suppress SF. Taken together, the
results on these two kinds of bridge support the idea of a strong gas density
dependence of SF in tidal features analogous to the surface density dependence
in isolated disks (e.g.,
Kennicutt 1989,
1990).
It seems very likely
that more precise conclusions about the SF process can be derived from careful
study and comparison of different types of bridge.
Let us return to the Arp 86 system, for a moment. In addition to wave
compression, the mass transfer onto the companion (NGC 7752) is likely to
result in gas accumulation at its center, eventually triggering enhanced SF.
The companion is in fact experiencing a strong burst of SF, and it has
sufficient gas to continue forming stars for 1-2 x 108
yrs. (Laurikainen et al.). Moreover, this gas is only a small
fraction of the total in the primary, so mass transfer in future encounters
could provide more fuel. Thus, this system provides a fairly extreme example
of how multiple encounters can lead to considerable galaxy evolution long
before the final merger.
On the other hand, the M51 companion shows little current SF activity
(Thronson et al. 1991),
though it shows Balmer absorption lines thought to
indicative of a "post-starburst" stellar population
(Ho, Filippenko and
Sargent 1995).
Joseph et al. (1984)
carried out a near-infrared study of
interacting systems that included six M51-type systems, and found most had
quite high infrared luminosities, though none were found to be as active as
Arp 86. If there is suppression and delay in the
accretion process, the
timescale is evidently smaller than the duration of enhanced SF.
Mihos (1994)
has recently reminded us of another factor affecting the
net SF in M51-type systems. Simulations have shown that
prograde interactions
frequently induce the formation of a bar component in the primary, which, in
turn, funnels gas to the center (also
Noguchi 1990,
and see sections 3.5,
5.4). Mihos' simulations suggest that
bar-driven SF is much greater than the
wave-driven SF in these systems. However, the timescale for the bar-driven SF
is generally much longer than that of the waves and bridges. Nonetheless,
like the "transients" considered in these chapters, this process
could have a substantial effect before the colliding galaxies merge.
One final topic to touch on here is mass transfer onto ellipticals or
very early-type disk galaxies, which are very gas poor. de Mello et al.
(1995,
1996
and references therein) have studied a number of these so-called
E+S mixed pairs, with the goal of determining what fraction are truly
physically associated, and what effects they have had on each other. Although
the statistics are still small, the answer seems to be that, among the
physical pairs, tidal morphologies are common. So too is evidence for a young
stellar component in the ellipticals, probably fueled by tidal mass transfer.
Part of the motivation for such studies was the discovery that
early-type galaxies are not devoid of gas. Space does not allow a recital of
the history of this discovery, or an explanation of why it was surprising to
many. However, it is now well-established that many ellipticals have at least
a small gas fraction, and S0 galaxies often have an (extensive) annular
neutral hydrogen disk located at a much larger mean radius than the stellar
disk (e.g.,
Lees et al. 1991,
1992,
Lees 1992
and references therein). Tidal
mass transfer was one of a number of possibilities considered as the source of
this gas, though it currently seems unlikely that this process is responsible
in most cases. On the other hand, the de Mello et al. studies, and an S0
example of
Appleton (1983),
suggest that it is important in some systems.
4.2. Complete Collisional Disruption
Complete collisional disruption is the ultimate transient event. As
elsewhere in nature, big ones eat little ones, i.e., small companions
generally suffer the most from tidal forces, and the transfer of orbital
energy to internal energy. This is certainly the case in the interaction
between the Magellanic Clouds and the Milky Way. However, the classical Roche
disruption criterion for a satellite orbiting a planet teaches us that other
factors, like the relative compactness (density), also play a role.
However, the IA theory is again more appropriate than the classical
theory of a secular process. Its application dates back to
Spitzer (1958),
who studied the tidal destruction of star clusters due to perturbations from
passing interstellar clouds. Spitzer used the IA to estimate the internal
energy change of the cluster, and compared this to its total binding energy.
Disruption is assumed to result when the magnitude of this ratio is of order
unity or greater.
McNamara et al. (1994)
have given a scaled version of this
ratio appropriate to the case of disruption of dwarf galaxies by large
primaries,
for disruption. In this expression, M1 is
the mass of the primary, Rdwarf is the radius
of the dwarf, P is the closest approach distance, Vp is the
relative velocity at closest approach, and V rms is the
"stellar velocity dispersion of the
dwarf prior to the collision." Detailed analytic formulae for the energy
transfer have been derived in a variety of special cases, much more discussion
of this topic can be found in the review of
Alladin & Narasimhan
(1982),
and references therein. Note that the IA estimate for the tidal capture, due
to transfer of orbital energy to internal energy, is very similar, but uses
the ratio of the orbital energy and its change. IA analytic estimates of the
transfer of angular momentum have also been derived in special cases, see
e.g.,
Sunder, Kochhar &
Alladin (1990),
and references therein.
In light of modern N-body simulations, which we will discuss in a
moment, the impulsive energy transfer criterion for disruption seems
unrealistically simple. It clearly neglects many processes, including angular
momentum coupling and dynamical friction (see below). If the perturbation is
nonlinear, the assumption that it is instantaneous is also unrealistic:
effects like tidal distension and dynamical friction will develop during the
encounter, and affect its outcome. Finally, the simple energy criterion
finesses the fact that galaxies consist of multiple components. Massive dark
halos bind galaxies much more tightly than was thought in the early days of
this subject, so at the least the primary mass factor in formula should
include the halo contribution. Nonetheless, Spitzer's formula remains useful
if only as a quantitative measure of how nonlinear is a given perturbation.
Yet, we still face a number of questions, and a possible paradox,
concerning collisional disruption. On one hand, there is observational
evidence for its occurrence. On the other hand, the existence of massive
halos makes it seem an unlikely event, and recent N-body
simulations confirm
the difficulty of destroying a companion in a single collision. On the
observational side, the case is easiest to make for very low mass companions
like the Magellanic Clouds and other dwarf companions of the Milky Way.
Dwarf companions are difficult to detect, so it is hard to find systems
actually undergoing disruption. But some possible examples have emerged. One
such is the Virgo cluster pair consisting of the Virgo elliptical NGC 4472,
and its extremely damaged dwarf companion UGC 7636 studied by
McNamara et al. (1994).
In the optical, the latter galaxy shows signs of extreme tidal
stress, including a large tail of debris. An HI cloud lies between the two
galaxies. McNamara et al. conjecture that the HI has been removed from the
dwarf by ram pressure stripping by the hot gas in the halo of the giant
elliptical. Radio observations indicate that the cloud is not
self-gravitating, and will ultimately sink into the elliptical. They also
conclude that the dwarf will be disrupted and dispersed.
McNamara et al. note the apparent contradiction between their findings
on this system and
Gallagher and Hunter's
(1989)
finding that, in a large
sample of Virgo cluster dwarf irregulars, there was little
evidence for major
alterations or destruction. However, they note that "only interactions
which result in .... an observable final state" could be detected.
Events like that the NGC 4472 / UGC 7636 are relatively short, and probably
leave little trace afterwards. Gallagher and Hunter's result is consistent
with this system if dwarfs are generally able to avoid their fate for a long
time, but the result is quick when it comes.
Another possible example, is suggested by the long HI plume extending
out of the ring galaxy in the Arp 143 system. Appleton et al.
(1987a,
b)
suggested that this may in fact be the remains of a recently despatched
gas-rich dwarf, destroyed in the collision which formed the ring.
Unfortunately, the presence of another large (early type) galaxy in the group
complicates the interpretation.
There are virtually no clear examples of companion disruption among
equal mass pairs, where we expect disruption to be difficult, but merging to
be rapid. The most intriguing cases should be those involving an intermediate
mass companion, but again few examples can be found in the literature.
Appleton, Pedlar &
Wilkinson (1990)
have provided an intricate example of
a possible near miss for an intermediate mass galaxy in the double elliptical
system NGC 5903 / 5898. Their 21 cm mapping showed a large mass (4.5 x
108 solar masses) of gas in a large region around
NGC 5903. This gas is in a state of extreme
disequilibrium, and probably
recently accreted. The other elliptical, NGC 5898, contains little HI, but
has an ionized gas disk that rotates in the opposite sense of its stars, and
so was also probably accreted at an earlier time. Appleton et al.consider the
possibility of a double accretion event. It seems unlikely that a single
dwarf would suffer such a spectacular two part death. However, it is also
possible that a disturbed spiral to the northeast was massive enough to
survive two collisions. The HI filaments near NGC 5903 do point in its
direction.
In sum, observations provide evidence that prompt disruption may occur,
but there are ambiguities in all particular cases. N-body
simulations inspire
a less sanguine view of the possibility of complete disruption in a single
collision. Unfortunately, the simulations are the most useful (and efficient)
for modeling collisions between galaxies of similar mass, rather than those
with mass ratios 3-4 orders of magnitude smaller, as in dwarf-giant
collisions. Yet we can expect simulations to provide very useful information
in the case of intermediate mass ratios, which is perhaps the most
interesting case.
The new simulations of head-on collisions by
Séquin &
Dupraz (1996)
provide especially good examples because they study cases with quite
small mass ratios, i.e., 1/10 and 1/20. A weakness of these simulations is
that each galaxy only contains one component, but if this is assumed to be the
dark halo, it seems unlikely that conclusions about disruption will be greatly
effected by the inclusion of other components. Their description of two
particular runs is of interest here. These runs use a 1/10 mass companion,
and are identical except that the companion in run F3 (diffuse) has twice the
scale length of that in run F1 (compact). In the diffuse run there is a great
deal of destruction in the first collision, and the companion is nearly
destroyed. The core of the compact companion in the other run survives
several collisions, and merger and disruption appear to occur simultaneously.
The authors analyse the roles of various processes (e.g., tidal shock,
distension, and dynamical friction) in detail, but they find that the amount
of mass loss in each encounter depends sensitively on the density ratio of the
two galaxies at closest approach. This conclusion is very reminiscent of both
the classical Roche criterion, and various factors in the Spitzer formula.
The paper of
Walker, Mihos, &
Hernquist (1996)
also studies the
merger of a 10% companion, but from an orbit with an inclination of only
30°. Multi-component galaxies (bulge-disk-halo) were used in this work.
The companion was quite compact, and its core did survive the merger, though
the authors find that the classical tidal radius (see BT Sec. 7.3) did not
predict the core size very well. This "sinking satellite"
situation, with little tidal shock, is much milder than the head-on collision
case (see section 5.2).
While these N-body papers confirm that reality is much more complex
than a simple criterion for tidal disruption, that criterion stands up as a
qualitative predictor. The N-body simulations also imply that the
probable
resolution to the "disruption paradox" is that it may take several
encounters to completely destroy a diffuse companion even in favorable cases,
where there is strong tidal shocking. Nonetheless, it is possible to do so
before the merger occurs. Yet research up to the present still leaves open
the question of how important this process, versus merger, is for dwarf
companions.
We have seen that the effects of a single impulsive collision, i.e.,
the transients, are complex, and have great morphological and dynamical
variety. They can also have a major effect on the structure of the galaxies
involved, especially the small galaxy in an unequal collision. However,
summed over the universe, their net impact on galaxy evolution is less than
that of mergers. Yet they are the inevitable prelude to merger. The first
collisions leading up to the merger can greatly modify the structure and gas
content of the merging partners. These modifications will be reflected in the
detailed structure of the merger remnant, as well as that of the tidal debris.
Thus, we expect merger remnants to be morphologically diverse, even if their
progenitors were not.
Studies of transients also provide clues to and checks on theories of
how merging happens. If the merging process had ended long ago, our
understanding of it would be much more incomplete and speculative. It is a
great advantage to be able to observe the diverse set of processes involved at
many different stages.
However, the study of transients does inevitably emphasize diversity.
Secular, dissipative, long-term dynamical processes stabilize galaxies and can
push them towards uniformity. We will consider these processes in the
following chapters.
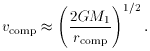

 will travel roughly
parallel to the companion during the interval
will travel roughly
parallel to the companion during the interval
 t,
and maintain a roughly constant distance,
t,
and maintain a roughly constant distance,
 r. Then the velocity impulse is about,
r. Then the velocity impulse is about,
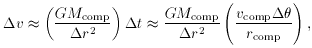
 v =
vesc do escape. The escape velocity is constant as a function
of radius for
a flat rotation curve galaxy. Then, that part of the primary disk contained
within the circle centered on the companion, with a radius of,
v =
vesc do escape. The escape velocity is constant as a function
of radius for
a flat rotation curve galaxy. Then, that part of the primary disk contained
within the circle centered on the companion, with a radius of,
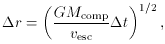
 r2, so
r2, so
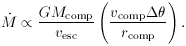

 should not
change with inclination angle i as long as the shape of the parabolic orbit
doesn't. If this is true, then its projection onto the primary disk plane,
which determines the impulse, scales as cos(i). Interestingly, the WS curve
of mass loss versus inclination is quite well approximated by the function 0.5
cos(i), except near i = 0°, and i = 90°. The factor 0.5 is the
fraction
of the disk that is positively torqued, and thus, roughly the maximum
mass loss.
should not
change with inclination angle i as long as the shape of the parabolic orbit
doesn't. If this is true, then its projection onto the primary disk plane,
which determines the impulse, scales as cos(i). Interestingly, the WS curve
of mass loss versus inclination is quite well approximated by the function 0.5
cos(i), except near i = 0°, and i = 90°. The factor 0.5 is the
fraction
of the disk that is positively torqued, and thus, roughly the maximum
mass loss.
 3-4. Even given that
vcomp
3-4. Even given that
vcomp  rcomp-1/2, a steep dependence of
rcomp-1/2, a steep dependence of

 on r is needed for the above formula to match this. Such a steep
dependence seems unlikely, and more likely the assumption that the particle
removal zone is a simple sector is not correct in the range of closest
approach distances where the mass loss changes rapidly.
on r is needed for the above formula to match this. Such a steep
dependence seems unlikely, and more likely the assumption that the particle
removal zone is a simple sector is not correct in the range of closest
approach distances where the mass loss changes rapidly.
 image of M51 of
Thronson et al. (1991)
shows that
its (apparent?) bridge is also forming new stars. So too is Arp 86 according
to the color data of Laurikainen et al., with an extremely blue region at its
end. Salo and Laurikainen's models for this system provide a detailed history
of the wave compression. There is qualitative agreement with the broad band
color data, assuming SF occurs in compressed regions, but this type of data is
not sufficient to allow a detailed reconstruction of the SF history and
spatial distribution.
image of M51 of
Thronson et al. (1991)
shows that
its (apparent?) bridge is also forming new stars. So too is Arp 86 according
to the color data of Laurikainen et al., with an extremely blue region at its
end. Salo and Laurikainen's models for this system provide a detailed history
of the wave compression. There is qualitative agreement with the broad band
color data, assuming SF occurs in compressed regions, but this type of data is
not sufficient to allow a detailed reconstruction of the SF history and
spatial distribution.