


This and the following chapter are devoted to the consideration of short term responses in galaxy collisions, i.e. those that occur shortly after closest passage. The examples below will be presented more or less in order of increasing disruptiveness. We begin with waves induced in disks, then take up large-scale mass transfer events, and finally the disruption of small companions. As discussed above, the often bizarre morphologies produced shortly after closest approach had a substantial impact on the early morphological groupings in catalogs; most of the nicknames below derive from those systems. Less obvious is the role of these transient features in the larger issues of collisionally enhanced (or suppressed) star formation, the merger process, and fueling active galactic nuclei (AGNs). In fact, their role is probably significant in all these cases, but they also provide unique signposts to help identify the nature of the interaction and the structure of the precursors. For example, the waves discussed below can provide a kind of seismological probe of the collisional galaxy.
In this chapter we consider in turn the types of waves induced in galaxy disks as a function of the spin-angular momentum coupling (whether +, - or 0). There is a great variety of disk waveforms, but the general structure of these waves depends more strongly on the angular momentum coupling than any other variable. We consider these waves "transients" because, generally, wave propagation times in disks are shorter than the companion return or merger timescales. Moreover, as we will discuss in later chapters, the processes of disk heating and phase mixing generally guarantee that waves will damp or disperse within a few propagation times.
There are several reasons for limiting our discussion to waves in disks. First of all, the constituents of bulge and halos have much larger random velocities than those found in disks, so unless the disturbance is large, waves rapidly diffuse. Here "large" disturbance means one that generates velocity perturbations comparable to the thermal velocities in these dynamically hot components. Such large disturbances are probably at least partially disruptive, and so, belong with the cases considered in the following sections. Secondly, halo oscillations have relatively long characteristic timescales.
The discussion in this chapter will also concentrate on two-dimensional waves in thin flat disks. Disk warping is undoubtedly an important effect of most collisions. We will also focus on stellar waves in this section, or on wave behavior that is common to both gas clouds and stars, but important differences will be noted in context.
P. N. Appleton and the author have recently completed an extensive review of this subject (1996, henceforth AS96), so I will limit this to a brief summary. (References are minimal in this section, but the reader can find many sources of more detailed information in that review.) Collisional ring galaxies are rare. They are the product of a nearly head-on collision between a D-type primary and a substantial companion, i.e. one with mass in the range 10-100% of the primary. A companion with much less mass would not have much of an effect on the primary, while one more massive than the "primary" is possible, but evidently unusual. The basic theory was worked out by Lynds and Toomre (1976, also see Theys and Spiegel 1976, 1977, and Toomre 1978). As the companion approaches and passes through the primary disk, stars and gas clouds assumed to be in circular orbits before the collision, are drawn inward by the extra gravity. As the companion moves away, the unbalanced centripetal force drives an outward rebound. The response is faster in the inner disk and slower in the outer disk, so stars still moving inward meet rebounders moving out, producing a compression wave which propagates outward. If the impact parameter is small this wave is a circular ring.
The Cartwheel galaxy, mentioned above, was probably the first ring galaxy discovered, and still is regarded as a prototype. This despite the fact that its progenitor was an usually late-type galaxy. The outer disk shows no evidence of old stars, though there is plenty of gas. It is also unusual in having two prominent rings, and the so-called spokes - spiral segments between the two rings (see Figure 4). However, there are a couple dozen collisional ring galaxies that have been studied in some detail, with many more candidates awaiting further study. Their progenitors span the whole range of Hubble disk types, e.g., from the "Sacred Mushroom" system, AM 1724-622, studied by Wallin and Struck-Marcell (1994, see Fig. 1) with a very early-type progenitor (e.g. an S0 galaxy) to the Cartwheel.
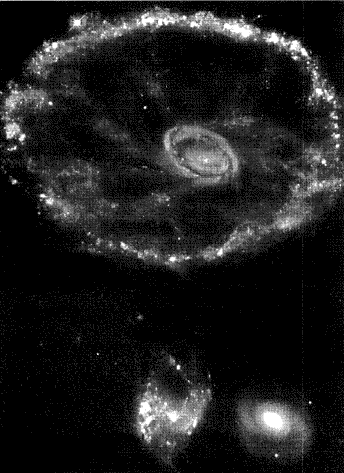
|
Figure 4. Hubble Space Telescope image of the "Cartwheel", a prototypical collisional ring galaxy (courtesy P. N. Appleton and NASA). |
Three fundamental facts make collisional ring galaxies a very important class, despite their rarity. The first is the symmetry of the collision that produces them. Because this symmetry is needed to produce a circular or nearly circular ring wave, once a collisional (e.g. expanding) ring is identified we immediately know a great deal about the collision. More precisely, there is a growing literature of comparisons between the collisional model and observation, and the general conclusion is that the collision theory is doing very well in accounting for observational features. (Though we note that there are other mechanisms for producing rings in galaxy disks, and we must have sufficient data to distinguish rings produced by these mechanisms before making detailed comparisons to collisional models.) On the other hand, nature has not missed a chance for an ironical twist. In a number of ring systems, the companion galaxy has not been identified. This is often because there are several possible suspects, which is not surprising since galaxies are commonly found in small groups.
The second fact is that the ring compression wave drives strongly enhanced star formation. Theys and Spiegel (1976) discovered that the rings in their modest sample frequently had blue colors indicative of massive young stars. Jeske (1986) and Appleton and Struck-Marcell (1987a) found that ring galaxy systems were relatively strong far-infrared emitters on the basis of IRAS observations. Now, observations of a number of systems in a variety of wavebands confirm the enhanced star formation in almost all cases, except those where the precursor was evidently an early-type, gas-poor disk (see Appleton and Marston 1997, and Appleton 1998 for an update of AS96). Insofar as density wave-driven star formation is understood (see e.g., the reviews of Elmegreen 1992, 1994b) this is not a surprise, strong compressions are supposed to trigger star formation. However, the details of this process are not well understood, and ring waves provide a relatively clean way to study them. In this case the Cartwheel is a prime example. The evidence suggests (e.g. Higdon 1993, 1995) that the ring wave is driving some of the first star formation to occur in the outer disk of the Cartwheel. Moreover, in the Cartwheel, Arp 10 and other systems, the intensity of the current star formation varies around the ring, which models suggest is the result of a variation in wave-strength following a slightly off-center collision. Thus, the ring waves provide a nearly direct confirmation that waves can induce vigorous star formation (i.e. a nonlinear response), and even within a single wave there are indications of a variation of response as a function of wave amplitude. Of course, this is also true in the much more common spiral density waves, but the generally more complicated spatial-temporal variations of those waves, and the effects of various resonances, make it useful to have a very different case like the ring waves to compare to. The range of companion masses implies a corresponding range in the strength of ring waves in different systems, potentially providing a great deal of information about wave-driven star formation from comparisons between systems.
The third fundamental fact is that if the collision is impulsive, and the companion relatively small, then the structure of the ring waves is primarily a function of the distribution of matter in precursor. Thus, ring seismology is possible. The amplitude, width, spacing between successive rings, and azimuthal variations in the case of off-center collisions, can be used to deduce the distribution of dark matter in the precursor. For example, widely spaced rings are a good indication of the presence of a massive halo (Struck-Marcell and Lotan 1990). In most ring galaxies we only see one ring, so the rings are definitely widely spaced, and most of the precursors probably had substantial halos. Models (Struck-Marcell and Higdon 1993) suggest that the Cartwheel is dominated by a large halo. If the collision is not impulsive (e.g., the relative velocity is low), ring seismology should still be possible, but the time-dependent perturbation will have to be modeled.
Let us return to the second point, star formation in rings, for a moment. At high resolution, such as that obtained by the Hubble Space Telescope observations shown in Figure 4, we have detailed information about where in the ring star clusters are formed (Appleton, priv. comm.). Even at lower resolutions, information can be obtained on the relative positions of young stars, old stars, and the gas clouds (Marston and Appleton 1995, Appleton and Marston 1997). For example, these authors find evidence that in large rings the ionized gas is concentrated on the outer edge of the old star wave. This data can provide powerful constraints on theories of the star formation process, and the gas/star wave dynamics.
One important complication, however, is that young star activity, i.e., winds, radiation and supernova explosions, may provide nonlinear feedbacks to the gas dynamics. For example, pushing some gas to the front of the wave, or out of the disk. Figure 4 provides some direct visual evidence for such effects, i.e. the interstellar gas represented by emission and reflection nebulae seems very frothy (to borrow the term of Hunter and Gallagher 1990). The filaments, arcs and shells are all likely consequences of the activity of the young star clusters (e.g., Heiles, Reach, and Koo 1996, and references therein), and in aggregate give a clear impression of turbulence. There are a myriad questions waiting to be addressed: How is this turbulence different from that in the interstellar gas of undisturbed galaxies (model examples of which are given in Passot, Vazquez-Semadeni, and Pouquet 1995)?, How well-developed is it, and over what range of scales does it extend before it is damped or frozen out in the rarefaction region behind the compression wave? How does the turbulence effect the star formation process which generated it? How does it effect the thermal phase balance in the gas? These are very difficult questions, relevant to many types of collisional galaxy, which have hardly begun to be explored. The relative simplicity of ring waves makes them an attractive locale for addressing them.
At this point, we will retreat from the complexities of turbulent gas dynamics, and review the simple theory of symmetric stellar waves excited in a planar disk by a collision. Special attention was given to this topic in the review of AS96, so I will omit many details. However, since the key concepts can be generalized and carried over to many other cases, a self-contained overview is needed here. There are three key elements to this theory: 1) an impulsive disturbance (e.g. Alladin and Narasimhan, 1982), 2) followed by epicyclic kinematic motions (Lynds and Toomre 1976), and 3) the development of nonlinear, caustic waveforms (Struck-Marcell and Lotan 1990). The first item actually has two parts: that the disturbance occurs very rapidly compared to other relevant timescales, and that the disturbance can be decoupled from the subsequent evolution. Simple (e.g. analytic) models are based on the idealization of an instantaneous disturbance, but they remain interesting even if this is only approximately true. If the disturbance is persistent, it can't be treated as part of the initial conditions of the dynamical equations, and in general, no conceptually simple model can be constructed. (However, this case can be treated with the perturbation theory described in Chapter 5.)
The first condition above is necessary, but not sufficient, for the second condition. The validity of a kinematic approximation to the motions of stars, gas clouds, and dark matter particles, depends not only on the prompt disappearance of the disturber, but on the constancy of the gravitational potential they move in. In principle, this potential is also perturbed by the collision. However, if it is dominated by a dynamically hot component, like the dark matter halo, and the perturber is not too massive, the halo disturbance may be small compared to that experienced by dynamically cold disk particles. Henceforth, I will refer to assumptions 1) and 2) together as the KIA (kinematic impulse approximation), and 1) as the IA.
If these approximations are valid, then we only need a description of the (kinematic) particle orbits to complete the theory. Depending on the form of the potential, the orbit equations will generally involve elliptical integrals (e.g., Grossman 1996). However, the ancient greeks developed a planetary orbital model that provides a very convenient conceptual and analytic tool here too. This is the famous epicyclic model, in which, the particle is assumed to orbit on a (small) circle, whose center orbits the potential center on a larger orbit. The epicyclic model was first extensively applied to galactic dynamics by Lindblad (1959 and references therein). If we assume circular orbits in the target disk before the collision, and that the impulsive disturbance in the symmetric collision is small (perturbative limit), then the effect of the collision on the orbit will be a sinusoidal oscillation about the initial, "guiding center" radius. That is, an epicycle. This is only an approximation when the disturbance is of finite amplitude, but the comparison of analytic and numerical models suggests that it can be a good one for transient waves.
The epicyclic orbit equations for a star are,
where r(q,t) is the instantaneous particle radius, q is the precollision
orbital radius, and A(q) is the amplitude of the epicyclic oscillations. In
the IA it is assumed that the collision is so rapid that the particles do not
move during it, but the force and acceleration induce a velocity change.
Thus, the initial radial velocity amplitude is the velocity impulse, and the
amplitude A is found by setting t = 0 in equation (3), A =
-
The radial motions of a collection of such particles, in a
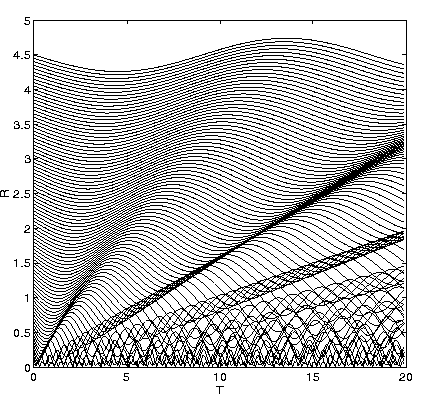
representative gravitational potential, are shown in
Figure 5. In the
particular case shown in Figure 5 it is assumed
that the companion to primary
galaxy mass ratio is 0.25 and that both galaxies have massive dark halos.
Specifically, the potential assumed for the primary galaxy gives a rotation
curve of the form v =
v(
Figure 5. Radius versus time for
representative stars in a kinematic model for a
collisional ring galaxy as described in the text.
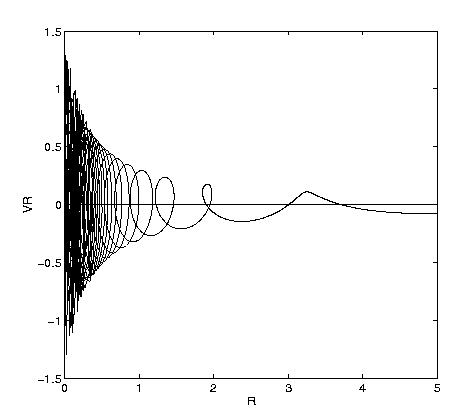
As stellar orbits at different radii get more out of phase, the orbit
crowding phenomenon becomes orbit crossing, and thus, the second and third
rings are broader than the first. (Ultimately, the rings overlap and become
effectively smoothed out by this "phase mixing".) This is shown in
Figure 6, which is a r - vr phase
diagram (after figures in
Struck-Marcell 1990a,
b)
with a phase mixed center, an orbit
crowding outer ring, and an isolated orbit-crossing ring between. The orbit
crossing rings are bounded by sharp edges. They are in fact caustics, formal
singularities in the stellar density.
Figure 6. Phase diagram of radial velocity
versus radius (r - vr) from the kinematic calculation of
Figure 5, at dimensionless
time t = 20. The loops are the result of orbit crossing in the inner ring,
while the positive velocity wave between radii of r = 3.0 - 4.0 shows the
orbit-crowding outer ring.
The conservation of mass in a thin cylindrical annulus implies that the
density is given by,
where
Generally, we do not expect the same wave structure in the collisional
(see section 1.2) gas component. The stellar
orbit crossing zone and its
caustic edges should be replaced by a dissipative shock wave. The gas will be
heated in this shock, but cooling times are short, and so as a first
approximation the shock can be assumed to be isothermal. In the first ring
this shock may be relatively weak, because the epicyclic motions in adjacent
radial zones are still nearly in phase. The shock in the second ring wave is
likely to be much stronger
(Appleton and
Struck-Marcell 1987b,
Struck-Marcell and
Appleton 1987).
Even so, the thermal physics and the observables are
likely to be dominated by the compression induced star formation behind
the shock.
Sometimes, however, the gas may behave more like the collisionless
stars, as discovered by
Gerber, Lamb, and Balsara
(1992)
in their simulational
study of Arp 147. This is the result of a very interesting
effect, when the
disk is warped by the collision, so gas clouds at different radii are able to
execute their radial epicyclic oscillations in different vertical planes, thus
becoming collisionless. The gas behavior in any particular situation depends
on whether the ratio of the radius of curvature of the warp to the local
epicyclic excursion is greater or less than unity.
3.3 Ring Relatives: Bananas, Swallows and
Others.
When collisions become less than perfectly cylindrically symmetric,
that is, as the impact parameter increases, the diversity of waveforms
increases rapidly. In this section I will illustrate this with a few
examples, and note how the theory described in the previous section is
generalized.
The consequences of a small increase in the impact parameter (relative
to the scale length of the gravitational potential) are not terribly dramatic.
The result is an asymmetric or partial ring, which looks like a crescent or
banana (see
Appleton and
Struck-Marcell 1987b,
Chatterjee 1986).
Theoretically, these crescent waves are nearly as simple as the symmetric
rings, at least for points at radii greater than the impact radius. There,
the impulse is still primarily radial, but generally with an amplitude that
depends on distance from the impact point. However, the radius of the
compression wave depends primarily on the epicyclic frequencies (in the
perturbation limit), so it is little different from the symmetric case. Thus,
in this approximation, the wave is still nearly circular, but with an
amplitude that varies with azimuth around the ring. (See AS96 for a more
complete description.) For the stellar component this means that the caustic
wave may not extend to all azimuths, i.e. there may be orbit crossing on the
"strong" side, but only orbit crowding on the weak side. As a
result the two circular caustic edges of the symmetric wave are replaced by
the crescent. Similarly we expect variable compression and shock strengths
around the ring.
As the ring propagates outward, the ratio of the impact radius to the
ring radius decreases, so the perturbation is more symmetric, and the crescent
ends join to form a (weaker) ring. This shown in
Figure 7 (from
Appleton and
Struck-Marcell 1987b).
Other numerical models of asymmetric rings can be
found in
Appleton and James (1990),
Gerber (1993), and
Struck-Marcell and Higdon
(1993).
Figure 7. Contour maps of the gas density
for a hydrodynamical simulation of an off-center galaxy collision
(Appleton and
Struck-Marcell 1987b).
Solid
contours indicate densities above the initial unperturbed value and dotted
contours show lower densities.
The overwhelming majority of real ring galaxies are asymmetric in
appearance. This includes both the Cartwheel and the very similar VII Zw 466
ring. Appearances can be a bit deceiving here, since optical/infrared
observations usually reflect the number of massive young stars and clusters.
The local star formation rate (SFR), and perhaps the stellar mass function,
are most likely nonlinear amplifiers of the wave compression. Examples of
galaxies with apparently strong crescents include the "Sacred
Mushroom" AM1724-622 (see Fig. 1),
and most of the objects on page 6.1 of the Arp-Madore photographic atlas.
The crescent is an evolving or "metamorphosing" caustic
structure, and thus, we can learn more about it from singularity or
catastrophe theory (see e.g.
Poston and Stewart 1978,
Arnold 1986).
While
singularity theory is not widely used in astronomy, it has found a couple of
niches. One of these is the Zeldovich "pancake" approximation for
galaxy and large-scale structure formation
(Arnold, Shandarin and
Zeldovich 1982),
where as a result of gravitational collapse, collisionless dark matter
particles form a full range of three-dimensional caustics or singularities.
An early, less well known application, is found in the work of
Hunter (1973)
on spiral density waves. Hunter found that wave characteristics
converged to singularities.
Caustics occur in (models of) a number of different types of
collisional galaxies. AS96 reviewed the application of singularity theory to
collisional galaxies, and suggested that the theory is more generally
relevant because,
In two and three spatial dimensions it offers a complete classification of
the generic, nonlinear waveforms and their possible evolutions... These
include cusps, swallowtails, and pockets or purses (see
Arnold 1986),
and overlapping combinations.
... (Moreover,) it significantly extends our conceptual model. It takes us
from models for individual stellar orbits to the structure of the nonlinear
density waves,... It makes us aware of "elementary" waveforms that
are more complicated than rings or spirals, and yet not intractably complex...
For example, beginning with a model for the orbits, like the kinematic impulse
approximation, we can derive analytic expressions for the location of the
caustics, which provide a skeletal outline of the waves for any particular set
of structural and collision parameters. (AS96)
The procedure for finding ring edge caustics described in the previous
section can be generalized with the goal of mapping the edges or
"skeletal outline" of the more general waveform. However, even
limiting consideration to waves in a thin, unwarped disk, three effects
complicate this formalism: 1) the azimuthal dependence of the
perturbation amplitude A, 2) the fact there is now an azimuthal
component to the velocity impulse (or a torque), and 3) even in the
limit that the gravitational potential is dominated by a rigid halo or bulge,
there is an impulse on the potential center. Items 2) and 3) may have a small
magnitude, but still have important effects. Because of effect 3) halo
particles at radii smaller than the impact radius will receive a net impulse
toward the intruder, while particles in a spherical shell at large radii will
not. Thus, the halo is apparently broken into two kinematic components,
though even this dichotomy is too simplified to realistically represent the
time-dependent potential. It seems that perturbation theory is rather shakey
unless the typical velocity impulse is smaller than the mean halo particle
velocities, i.e. the halo is too hot to be significantly perturbed.
We will adopt this hot halo assumption for the moment (but see the analysis of
Gerber and Lamb 1994
which does not). Then following AS96 we can
write the approximate kinematic equations as,
These epicyclic orbit equations are very similar to equations (2) and (3).
The chief difference is that, as a result of the azimuthal velocity impulse,
the epicycle is centered on a new guiding center of radius q'. The initial
particle radius q is generally different from q', so this introduces an
initial phase
AS96 describe a limiting case of this equation that has
"crescent" solutions, and probably contains other waveforms as well.
Struck-Marcell (1990a),
Donner, Engstrom, and
Sundelius (1991),
and
Gerber and Lamb (1994)
all used numerical models to study the creation of
waves in disks of particles following kinematic orbits like those of equations
(5). Donner et al. also numerically solved the caustic determinant equation
(6) in specific cases to compare to numerical models. Donner et al. (in
planar collisions), and Gerber and Lamb (in collisions nearly perpendicular to
the target disk), both found good agreement between the kinematic models and
self-consistent N-body simulations at early times. Thus, providing evidence
that the effects of the time varying gravitational potential take some
time to accumulate.
Struck-Marcell (1990a)
and Donner et al. both found evidence for the
development of higher order caustics like the cusp, swallowtail and
pocket/purse (see
Arnold 1986)
in their calculations. Perusal of the
photographic atlases shows many sytems that appear to match the nonlinear
waveforms, but this is very circumstantial evidence. M. Kaufman and
collaborators (including the author) are investigating two galaxies that have
the appearance of swallowtails (NGC 3145 and NGC 5676) with radio (21 cm) and
optical observations, but the results are not yet complete. We are
specifically searching for the high velocity dispersions or gaseous shock
waves that would characterize the stellar orbit crossing region.
Wallin and Struck-Marcell
(1994)
compared caustic models to the broad
crescent wave in the early-type ring galaxy AM1724-622 (the "Sacred
Mushroom"). Interestingly, the crescent was best matched by models with
a declining rotation curve in the precursor. Though somewhat unusual, this
might be the result of the gravitational potential in the disk being dominated
by the strong bulge component. It was hoped that it would be possible to
determine if the broad ring edges were in fact sharp caustics, or if not,
obtain some measure of the effect of diffusive smoothing processes.
Ultimately, such processes, together with phase mixing (see previous section)
and the overlap of multiple caustics, will erase all traces of caustic waves
in the disk. However, the published simulations indicate that these processes
do not strongly effect the first couple of waves. Because of the limited
resolution of the data, and the fact that dozens of foreground stars cover
this galaxy, which lies near the galactic plane, this study was not
definitive. Hubble Space Telescope observations might be able to
surmount the difficulties.
The caustics theory for nonlinear waves in collisional disks is still
relatively young and untested. Many questions have not yet been fully
addressed, including how far can the analytic models be pushed before they
become too inaccurate or too algebraically complex to be useful?
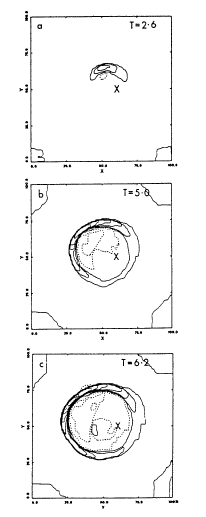
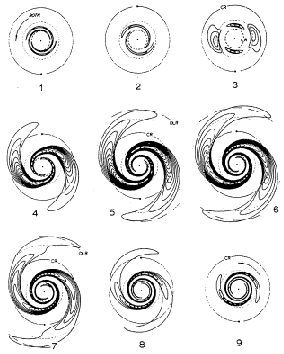
Toomre (1978)
discovered that, as the impact point in a vertical
collision is moved out from the disk center to its edge, the ring wave
metamorphoses into a spiral. Toomre used a sequence of restricted three-body
models (reproduced in Fig. 8) to demonstrate
this. Several remarkable and
instructive points can be taken from this figure. The first, noted by Toomre,
is the disks are not destroyed in any of these cases, though they do suffer
significant time-dependent warping or flapping. This result, along with most
of the other qualitative features of Figure 8
are confirmed in an analogous
series of fully self-consistent star-plus-gas simulations run by
Gerber (1993).
There are differences, but they are modest given the different
simulation techniques and the different structural characteristics in the
initial galaxies. (I.e., a rigid point-mass potential in Toomre's versus an
initial flat rotation curve structure in Gerber's.)
Figure 8. Toomre's ring-to-spiral
transition is illustrated by a sequence
numerical model evolutions with progressively decreasing companion impact
radii. Each row shows a different model. See text and
Toomre 1978 for
details.
Secondly, these simulations clearly show caustic edges, and in some
cases they appear quite complex. We would hope that these waveforms could be
explained by the KIA-caustics theory, but to date no detailed analysis has
been done. However, some qualitative aspects can be explained by this theory
with little effort. To begin with the line connecting the target disk center
and the impact point is a key division. Ahead of this line one component of
the velocity impulse will be directed against the particles' rotation
velocity, so these particles will be slowed and fall inward. Behind this line
particles will have their tangential velocity increased, so they will fly
outwards. The infalling particles will compress, forming a region of enhanced
density. In fact, since the backward impulse increases to some maximum as
azimuth increases from the division line, we can expect an orbit-crossing zone
in this compressed region if the impulse is great enough. Thus, in general, a
"lips" (crescent) caustic will form and shear into the leading edge
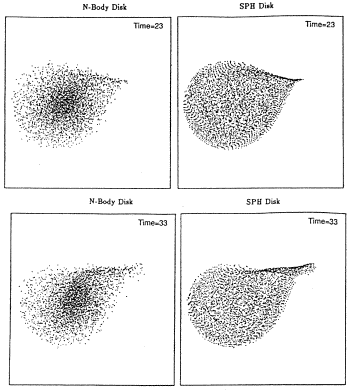
of a spiral wave. This feature can be seen in the more off-center of Gerber's
model collisions, and in his model Ring4, the wave is strong and caustic-like
edges are especially apparent in the dynamically cooler gas particles (see
Fig. 9).
Figure 9. A self-consistent, N-body plus
Smoothed Particle Hydrodynamics
simulation from R. A. Gerber's thesis, showing an incipient spiral in a
collision like those that produce ring galaxies. In this case the trajectory
of the companion galaxy was nearly perpendicular to the primary disk, and the
point of closest approach was at the edge of that disk (see
Gerber 1993
for details).
We can sketch a quick derivation of this wave from the KIA caustics
theory (neglecting the perturbation of the potential center of the disturbed
galaxy). The azimuthal impulse can be written,
where
At each radius, and on each side of the center-to-impact line, there is
some azimuth where |
For simplicity, assume that the potential of the perturber is that of a
simple point mass. Then the equation
ð
which depends only on the parameter r*/q.
For impacts within the disk, this spiral kinematics is superimposed on
the radial kinematics discussed above. Figure 8
shows that as the impact
point moves out of the disk, the radial ringing diminishes in importance, and
tidal stretching becomes more important.
Note that this is a very nonstandard description of a spiral
wave in a galactic disk. The caustic spiral is a nonlinear transient, so
there is no obvious connection to the classical quasi-stationary (linear)
density wave theory (see e.g.
Binney and Tremaine 1987;
ch. 6,
Palmer, 1994,
ch. 12). Swing amplification is another process that plays a very important
role in interaction driven waves (see
Toomre 1981
and below), but in this case
there has not been time for significant amplification. This wave is simply
the result of correlated initial conditions, and a special aspect of the
direct collision is that it is truly impulsive. This example also provides an
interesting illustration of the transition from the study of ring waves to
more standard tidally induced waves.
3.5. Tidal Spirals and Oculars (YDx+)
The class YDx+ includes encounters in which the companion galaxy flies
by in the plane of the primary disk, and in the same orbital sense as the disk
rotation, and with a point of closest approach generally located outside the
disk (i.e., prograde collisions). It seems odd at first that these collisions
can result in more damage than nearly head-on vertical collisions, but the
tidal perturbation is sustained for a longer time in this case. The result is
the formation of the great bridges, tails and strong spirals hinted at in
Holmberg's work, emphasized by Zwicky, and shown convincingly to be tidal
remnants in the work of the Toomres and others in the early 70s (see Chapter
1). In this section we will consider the strong spirals, and leave bridges
and tails to later sections.
The great "Whirlpool" galaxy M51 is the prototype of these
collisional spirals (see Fig. 10 and section 9
of the Arp-Madore atlas). It
is also a bridge/tail galaxy, with a connected companion that has attracted
much attention in the interacting galaxy literature. At the same time, it has
also been a prototype in the spiral density wave literature. The possible
connection between the inner and outer phenomena was discussed by the Toomres
(1972, also
Toomre 1974),
but the idea encountered difficulties
(Toomre 1978).
While there was some evidence for tidal influence on the inner spirals in the
21 cm observations, the restricted three-body simulations didn't produce any
such waves. However, by 1980 Toomre had discovered the missing piece of the
puzzle in "swing amplification".
Figure 10. Optical image of the
"Whirlpool galaxy" M51, whose beautiful
spiral arms are likely a result of the ongoing collision, see text. (Digital
Sky Survey image courtesy of AURA/STScI.)
Swing amplification, as described by
Toomre (1981),
depends on the near
commensurability of the shearing timescale and the epicyclic (compression)
timescale, which is common in galaxy disks. This commensurability works to
keep stars in the overdense region for relatively long times, which gives
self-gravity the time needed to greatly amplify the density contrast of a
spiral wave. Toomre used self-consistent N-body simulations to demonstrate
the operation of the process, and simple, "shearing sheet",
kinematic models to illustrate the role of the three main component processes:
epicyclic "shaking", wave shear and self-gravity. The original
paper gives a very clear presentation and other pedagogical summaries can be
found in
Athanassoula (1984) and
Binney and Tremaine
(1987, ch. 6.3). The
discussion here will be very brief, and more details on all the topics covered
can be found in these sources. For a recent technical review see
Tagger, Sygnet, and
Pellat (1993).
The amount of amplification is surprising - factors of between a few
and a hundred resulting from external perturbations of a few percent or less.
Toomre points out that the basic process was understood in work on spiral
waves carried out more than a decade earlier, but its amplification ability
was not. However, the nonlinear wave is generally short-lived, building up to
maximum amplitude within about one disk rotation time, and then winding up and
decaying on a comparable timescale. These points are illustrated in
Figure 11
from Toomre's paper. If the structure of the galaxy disk is such that it
possesses an inner Lindblad resonance, then the wave is "absorbed"
at the radius of the resonance. Lindblad resonances occur where the epicyclic
frequency is commensurate with the wave pattern frequency in the local
rotating frame.
Figure 11. The development of a
"swing-amplified" trailing spiral wave
from an initially leading wave from
Toomre (1981).
Contours represent fixed
fractional excess surface density, and the time between snapshots is one half
of the rotation period at the corotation point.
If there is no inner Lindblad resonance, the trailing wave can
propagate to the disk center, and reemerge as a leading wave. This leading
wave is sheared around into a trailing wave, and in the process, another round
of swing amplification occurs. The amount of amplification depends on two
parameters. The first is the Toomre Q parameter, which is a measure of how
close to gravitational instability the unperturbed disk is. The second
parameter Toomre called X =
If the wave can traverse the amplification feedback loop, numerical
models show that the end result is a global bar instability. This is an
extremely important consequence of a collisional disturbance. However, it is
not a transient event, so we defer further discussion to later chapters.
Another feature of the models in Toomre's paper was that the spiral
wave started from the center and moved out to include a large part of the
disk. This phenomenon offers hope that there would be time for large-scale
tidal features to develop, as in M51, before the prominent spirals disappear.
In sum, these discoveries bode well for the idea that strong inner spiral
waves can be driven by tidal encounters. Unfortunately, the M51 story has not
yet ended happily ever after.
Extensive 21 cm. observations
(Appleton, Foster and
Davies 1986,
Rots et al. 1990)
revealed unexpected HI features, including a long southern tail
coming off the (outer) western arm, and gas clumps north of the companion.
These discoveries coincided with the implementation of a new generation of
N-body and gas simulation codes (see e.g. Sellwood 1987, and
Barnes and Hernquist
1992a),
so it is not surprising that a number of new modeling
efforts were initiated. These include
Hernquist (1990),
Howard and Byrd (1990) and
Sundelius (1990),
and more recently,
Toomre (1994) and
Byrd and Salo (1995).
The models of Barnes, Hernquist and Toomre are based on a
passage of a companion on a high eccentricity orbit, while Byrd and
collaborators favor two disk passages to account some of the morphological
details of the system.
Barnes and Hernquist (1992)
conclude - "At
present, however, none of the calculations offer a really convincing
reconstruction of M51's spiral structure ... " (see also the
discussion of
Barnes 1998).
To compound the modeler's difficulties, new high resolution,
multiwaveband observations are being acquired at a steady rate, and they
reveal not only more detail, but new phenomena. These include the
distribution of ionized, atomic and molecular gas, and star formation across
the disk, and especially in the spiral waves (see reviews of
Rand and Tilanus 1990,
and Casoli 1991,
as well as the other observational reports in
Combes and Casoli 1991).
Casoli (1991)
discusses how the sequence of dense cloud
buildup, star formation, and subsequent cloud disruption is displayed as
expected across one spiral arm, but does not follow this sequence elsewhere.
Another example is the recent discovery from infrared imaging that the spirals
go deep into the central regions, and wind through three full revolutions
(Zaritsky, Rix, and Rieke
1993).
The infrared observations also revealed a
small bar in the inner regions. These phenomena, together with the
large-scale structures, will undoubtedly continue to challenge modelers for a
long time yet.
We should not, however, let the details of the M51 system distract us
from the general result - that even moderate collisional disturbances can
stimulate the formation of strong spiral waves via nonlinear amplification
processes. With perfect hindsight, we can see that this is just what was
required for M51 types, not only to explain the waves, but also
their presence
in a disk that does not appear highly disturbed (except in the outer regions).
Stronger disturbances bring more wholesale distortions. This point is well
illustrated by the ocular galaxies, first studied by
Elmegreen et al. (1991).
Elmegreen et al. define the ocular as "a bright oval approximately
one-half the size of the galaxy centered on the nucleus with a right angled
vertex at each end of the major axis, and spiral arms extend smoothly from
each of the flatter sides of the oval..." At first glance the ocular
seems to be a relatively pure result of tidal forces, with the oval resulting
from tidal compression, while the spiral arms result from tidal stretching
plus shear (see Fig. 12 and the images in
Elmegreen et al. 1995).
The fact
that the ocular persists for only about one rotation reinforces this
impression. However, the ocular is not simply the result of a homologous
compression. Unlike the initial unperturbed disk the ocular has sharp,
caustic edges ( in the models).
Figure 12. The collisional system
NGC 2207 / IC 2163 illustrates the ocular
waveform. Specifically, the disk of the smaller galaxy (IC 2163) has the
characteristic eyelid shape and the double-branched spiral arm. The other
spiral arm has been hidden or disrupted by the larger galaxy. (Digital Sky
Survey image courtesy of AURA/STScI.)
The ocular is formed in prograde collisions where the perturbation is
relatively strong, so the azimuthal impulse is substantial. Moreover, it is
clear that the sharp edge on the companion side forms first, and it appears in
the quadrant ahead of the line connecting the companion to the primary center.
Thus, it appears that stars are pulled ahead in the near side quadrant behind
the line of centers, and they swing out to apoapse in the leading quadrant,
where they are also pulled backwards by the companion. A mirror image process
occurs in the other half of the disk, but as a result of the interaction
between the stars and the swinging potential center of the primary. It would
be interesting to see the trajectories of stars that make up the ocular, but
these have not yet been presented in the literature. It would also be
interesting to see if the ocular form could be captured in a KIA model. This
would probably require an instantaneous approximation to the swing imparted by
the primary center as well as the companion.
Elmegreen et al. also found that the formation of an ocular depends on
a tidal strength parameter,
where 3.6. Fan Galaxies and One Arms (YDx-)
Retrograde collisions have never inspired the same interest as prograde
collisions. They do not form beautiful two-armed spirals.
Toomre and Toomre (1972)
included a retrograde encounter among their four numerical examples,
but concluded that the effects were "remarkably mild".
Eneev et al (1973)
presented a simulation that gives a very different impression, probably
because the perturbation was stronger. However, they did not discuss the
morphology of this model. In summarizing the retrograde encounters in their
atlas of N-body simulations of galaxy interactions,
Howard et al. (1993)
state that they "produce only broad fanlike global patterns, but rich
small-scale internal structure."
This is not to say that retrogrades were entirely overlooked in the
colliding galaxy renaissance of the 70s.
Kalnajs (1975) and
Athanassoula (1978)
studied the idea that a companion in a retrograde orbit could stimulate
the formation of a leading spiral wave (i.e. one whose outer end points in the
direction of disk rotation).
Kalnajs (1975)
presented evidence that M31, the
Andromeda galaxy, possessed such a one-arm. This work was followed up by the
study of
Thomasson et al. (1989),
which included analytic work, numerical
studies, and a comparison to observation. These works suggested that the
one-armed spiral wave is the result of the 1:1 orbital resonance, at which
orbits close after one radial oscillation. This resonance plays a role
similar to that of the 2:1 Lindblad resonance (two radial oscillations to
closure) in the case of the two-armed trailing pattern generated in
prograde collisions.
On the face of it the preceeding sentences seem strange. If the radial
epicyclic oscillation period depends primarily on the intrinsic mass
distribution in the disk galaxy, then how can the number of radial bounces
depend on the orientation of the perturber's orbit. This would be no problem
if the two types of wave appeared in different parts of the disk, but the
simulations show that they both can involve a considerable fraction of the
disk. The answer to the paradox is that the orbit closure statements refer to
a reference frame rotating with the wave pattern. In general, the stellar
orbits are precessing ellipses that don't close in an inertial frame, but as
Figure 3 of Thomasson et al. shows closure is nearly achieved in the wave
frame (also Figure 16 of
Athanassoula 1984).
It is worth a little further digression on this point, which is a
matter of fundamental kinematics akin to others considered in this chapter.
Consider, for example, a flat rotation curve galaxy, in which the rotation
velocity v = constant, the rotation frequency
In the two-armed case, the star begins at minimum radius in one arm,
and meets the second arm at the next minimum if that arm has also advanced (in
the same direction) by about 75°. Because this wave is moving in the
rotation direction, it must be trailing to maintain coherence at all radii.
We have discussed above how the tidal perturbation in a prograde collision
induces the two-armed wave. The one-arm mode is probably excited in
retrograde collisions simply because it is the lowest order leading mode.
Thomasson et al. find that the one-arm persists for several disk
rotation times, i.e. about as long as the typical collision-induced two-arm
pattern. The question then arises - why are there so few examples to be found
in the observations. The authors consider a variety of possible answers.
They favor a somewhat indirect explanation. A large halo-to-disk mass ratio
makes a galaxy stable against Swing Amplification of the m=2 mode. On the
contrary, they suggest that this mass ratio may commonly be low, enough to
give the m=2 mode a competitive advantage. It appears that the halo they are
referring to is that contained within the radius of the stellar disk. This
"halo" should also include a bulge if present.
Thomasson et al. also find that the retrograde disturbance has a
steeper dependence on separation (1/r4) than
the usual tidal force, and that it takes a substantial disturbance to produce
the leading arm. Retrograde collisions with small disturbances produce m=2
trailing arms or combined m=1 leading and m=2 trailing patterns. "Rich
internal structure" indeed.
Another possible example of this richness is the galaxy NGC 4622,
modeled by
Byrd, Freeman and Howard
(1993).
This galaxy possesses an inner
leading arm, a ring, and the two outer trailing arms. Byrd et al. found that
such features could be produced following a small impact parameter collision
with a low mass companion, orbiting in either direct or retrograde senses.
However, the retrograde collisions produced the better match to the
observed morphology.
A final note on leading one-armed waves -
Lotan-Luban (1990)
carried
out a series of restricted three-body simulations which showed that head-on,
low impact parameter collisions (like those that produce ring galaxies) can
produce a long-lived one-arm spiral. Generally, this spiral becomes prominant
after several ring waves have propagated through the disk, and the ringing has
pretty well phase-mixed away. By varying the potential structure she
confirmed Thomasson et al.'s result that a substantial halo component is
needed to produce the one-arm. She also varied the companion to target mass
ratio and found that intermediate mass companions produced the strongest wave.
This is not too surprising - high-mass companions caused much disruption in
the test particle disk, and low-mass companions didn't produce a sufficiently
strong perturbation. Thirdly, she carried out a series of simulations with
varying impact angle from head-on (small impact parameter) to in-plane
retrograde (with impact parameters greater than the disk radius). Of these,
the head-on small impact parameter collisions produce the strongest one-arm
waves. This helps account for the fact that some of her simulations seem to
make stronger and longer lived waves than those of Thomasson et al. The
retrograde planar waves are similar in both works.
Unfortunately, Lotan-Luban's work has not been redone with
self-consistent N-body simulations. This is especially important for testing
the longevity of these waves.
Most of the discussion above, and in the literature, on collisional
wave morphologies concerns stellar waves. Low amplitude, transient waves
mainly depend on kinematics, so to first order there is no significant
difference in the behavior of the interstellar gas and stars. However, in
nonlinear waves we expect caustic waveforms to develop in the stars and
dissipative shocks to develop in the gas. Dissipation could lead to some
separation of the two components, unless the gas disk is highly warped or
distorted. However, observations have not yet provided any compelling
examples of separation in waves, perhaps because strong perturbations lead to
highly distorted disks. Extreme separations may occur on large scales in
mergers, and large quantities of gas can be funneled to the center (e.g.,
Negroponte and White 1983,
Noguchi 1987,
1990,
Barnes and Hernquist 1991,
1992a),
at the same time that gas and stars can be thrown out to great
distances to form separate shells and ripples (e.g.
Hibbard 1995,
Hibbard & van Gorkom
1996
and references therein). These topics are
discussed below.
A large-scale, but less violent, example is provided by the galaxy
NGC4747 (Arp 159)
studied by
Wevers et al. (1984),
whose HI disk seems to have
been twisted relative to its stellar disk by 11° in projection! Exactly
how this occured remains a mystery, but given the distortions of the outer HI
disk of its companion NGC4725 it may well be that a direct collision with a
modest impact parameter was involved. In that case, direct cloud collisions
might have contributed to the separation, as well as dissipative accretion of
gas from the partner, described in the next section. There we will also meet
some milder examples of gas-star separation in waves and tidal structures.
In nonmerging collisional galaxies important differences between
stellar and gas dynamics result from heating and cooling effects. Young stars
winds, UV photoheating, and supernova blasts can heat and push the gas, and
disrupt cold clouds. At the least this can boost gas to greater heights above
the disk, i.e. making a thick gas disk. This is evident in recent simulations
of ring galaxies that include heating and cooling
(Struck 1997),
though it is
a transient effect in that application. The disk gas cools and settles on a
timescale comparable to the wave passage time. A more spectacular heating
phenomenon is that of superwinds generated by nuclear starbursts
(Heckman et al. 1993,
Lehnert & Heckman
1996).
Collisional galaxies may frequently
experience a nuclear starburst phase, driven by gas inflow resulting from
dissipation in waves and induced bars (see below).


 vr / q
vr / q . The
epicyclic frequency
. The
epicyclic frequency  depends on
the structure of the gravitational potential
(Binney and Tremaine 1987,
section 3.2.3), and
generally goes in the sense of longer periods at larger radii. This is the
origin of the ring compression, which, as noted above, results when outwardly
rebounding particles meet infalling particles from larger radii (as a result
of the longer epicyclic periods of the latter).
depends on
the structure of the gravitational potential
(Binney and Tremaine 1987,
section 3.2.3), and
generally goes in the sense of longer periods at larger radii. This is the
origin of the ring compression, which, as noted above, results when outwardly
rebounding particles meet infalling particles from larger radii (as a result
of the longer epicyclic periods of the latter).
 )
(r/
)
(r/ )1/n,
where
)1/n,
where  is a constant scale-length. A large value of n (n = 20) is used to
make v nearly constant. It is further assumed that the amplitude of the
collisional disturbance is constant with radius. Dimensionless units are
used, where the scale-length of the graviational potential
is a constant scale-length. A large value of n (n = 20) is used to
make v nearly constant. It is further assumed that the amplitude of the
collisional disturbance is constant with radius. Dimensionless units are
used, where the scale-length of the graviational potential
 , and the product GM(g) have been set to unity.
, and the product GM(g) have been set to unity.

 o(q) is
the initial, unperturbed density profile. Equation (4) applies to regions
with a single star stream. In orbit crossing zones (e.g., the inner rings in
Figs. 5, 6), the right
hand side must be replaced with a sum over terms for
each star stream. Singularities occur wherever ðr / ðq
= 0, i.e. where the particles some
initial radial range
o(q) is
the initial, unperturbed density profile. Equation (4) applies to regions
with a single star stream. In orbit crossing zones (e.g., the inner rings in
Figs. 5, 6), the right
hand side must be replaced with a sum over terms for
each star stream. Singularities occur wherever ðr / ðq
= 0, i.e. where the particles some
initial radial range  q are
squeezed into zero
volume,
q are
squeezed into zero
volume,  r = 0. Then, formally,
r = 0. Then, formally,
 ->
->
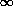 , though infinite densities
will not occur in real galaxies with finite numbers of stars. Substituting
the orbit equation (2) into the caustic condition, allows one to derive an
equation for the location of the caustic edges. This, together with equations
(2)-(4), provides the basis for a complete analytic model of stellar waves in
ring galaxies (see AS96 for details). We will see in subsequent sections how
the three elements of this theory can be generalized to less symmetric cases.
, though infinite densities
will not occur in real galaxies with finite numbers of stars. Substituting
the orbit equation (2) into the caustic condition, allows one to derive an
equation for the location of the caustic edges. This, together with equations
(2)-(4), provides the basis for a complete analytic model of stellar waves in
ring galaxies (see AS96 for details). We will see in subsequent sections how
the three elements of this theory can be generalized to less symmetric cases.

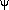 . The epicyclic
frequency is
. The epicyclic
frequency is  ' =
' =
 (q'), and the mean
angular velocity is
(q'), and the mean
angular velocity is
 cir(q'). The
amplitude A is a function
of radius and azimuth. Using the
initial conditions (in the IA), and the force balance equation for the guiding
center, the perturbed (primed) quantities can be eliminated in favor of
pre-collision values and the velocity impulses (see AS96). Then, in this
two-dimensional case, the infinite density caustic condition is given by
setting the Jacobean determinant equal to zero,
cir(q'). The
amplitude A is a function
of radius and azimuth. Using the
initial conditions (in the IA), and the force balance equation for the guiding
center, the perturbed (primed) quantities can be eliminated in favor of
pre-collision values and the velocity impulses (see AS96). Then, in this
two-dimensional case, the infinite density caustic condition is given by
setting the Jacobean determinant equal to zero,



 is the azimuth of a disk
particle
relative to the center-to-impact point line, and r* is the
impact radius, and R is the distance between disk particle and
the impact point (see SM90, AS96). R is related to r*, and
the particle's unperturbed radius q by the law of cosines,
is the azimuth of a disk
particle
relative to the center-to-impact point line, and r* is the
impact radius, and R is the distance between disk particle and
the impact point (see SM90, AS96). R is related to r*, and
the particle's unperturbed radius q by the law of cosines,

 v
v | is a maximum. Physically,
particles located at these
extremal azimuths feel the strongest pull backward (or forward) in their
orbits, and so, would seem to be likely participants in the formation of an
orbit crossing zone. More formally, the term
ð
| is a maximum. Physically,
particles located at these
extremal azimuths feel the strongest pull backward (or forward) in their
orbits, and so, would seem to be likely participants in the formation of an
orbit crossing zone. More formally, the term
ð /
ð
/
ð 0 in the
caustic condition (6) is proportional to
ð
0 in the
caustic condition (6) is proportional to
ð v
v /
ð
/
ð 0.
Therefore, if the cross terms in equation (6) are small, the zeros of these
derivatives yield caustics.
0.
Therefore, if the cross terms in equation (6) are small, the zeros of these
derivatives yield caustics.
 /
ð
/
ð 0 = 0 reduces
to a simple quadratic for cos(
0 = 0 reduces
to a simple quadratic for cos( ),
),

 v
v itself depends on the mass of
the perturber and other variables.
In the small radius limit, q -> 0, the
solution is
itself depends on the mass of
the perturber and other variables.
In the small radius limit, q -> 0, the
solution is  =
±90°. When r*/q is about unity,
cos(
=
±90°. When r*/q is about unity,
cos( )
)

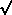 3 - 1, or
3 - 1, or

 45°. The full solution curve to equation (9) spirals out from
small radii to a nearly linear form at larger radii. Rotational shear will
turn this linear feature into a spiral. Qualitatively, this result seems much
like the behavior of the numerical models.
45°. The full solution curve to equation (9) spirals out from
small radii to a nearly linear form at larger radii. Rotational shear will
turn this linear feature into a spiral. Qualitatively, this result seems much
like the behavior of the numerical models.

 /
/  crit, where
crit, where
 is the
(unwrapped) spiral pattern wavelength, and
is the
(unwrapped) spiral pattern wavelength, and
 crit is critical
wavelength for gravitational instability. Note that
Q, X and
crit is critical
wavelength for gravitational instability. Note that
Q, X and  crit are
all defined as local quantities, though they typically do not vary drastically
across a galaxy disk. X and
crit are
all defined as local quantities, though they typically do not vary drastically
across a galaxy disk. X and
 depend on the number
of spiral arms in the global pattern, and since the amplification is very
sensitive to the value of X, significant amplification can only occur when
there are no more than a few arms.
depend on the number
of spiral arms in the global pattern, and since the amplification is very
sensitive to the value of X, significant amplification can only occur when
there are no more than a few arms.


 T is the time it takes
the companion to
travel through one radian relative to the primary, and T =
(Rgal3 / GMgal)
1/2. (Compare to equation (1) derived from the
IA.) Their two-dimensional simulations showed that oculars only formed when
the value of this parameter is greater than 0.019. For lower values,
substantial spiral waves are still produced, but there is not enough
transverse compression to produce the eye shape. They also found that when S
> 0.038, the ocular galaxy evolves into a barred galaxy, and beyond the YD+
stage considered here.
T is the time it takes
the companion to
travel through one radian relative to the primary, and T =
(Rgal3 / GMgal)
1/2. (Compare to equation (1) derived from the
IA.) Their two-dimensional simulations showed that oculars only formed when
the value of this parameter is greater than 0.019. For lower values,
substantial spiral waves are still produced, but there is not enough
transverse compression to produce the eye shape. They also found that when S
> 0.038, the ocular galaxy evolves into a barred galaxy, and beyond the YD+
stage considered here.
 = v/r, and the epicyclic frequency
= v/r, and the epicyclic frequency
 =
=
 2
2
 . This means that in an
inertial frame a
star goes around a bit less than 3/4 of a circle (255°) in one radial
period. Let us suppose, that the wave is defined by stars at a given
epicyclic phase, e.g., at minimum radius (point of greatest radial
compression). In the case of the leading one-arm this means that the wave
pattern merely has to travel (counter to the rotation) through an angle of
about 105° to meet the star again at minimum radius, and thus, close the
orbit in the wave frame. The wave must be leading because stars at larger
radii take longer to traverse their 255° of azimuth, by which time the
inner wave has traveled more than 105° (i.e., farther
"backwards").
. This means that in an
inertial frame a
star goes around a bit less than 3/4 of a circle (255°) in one radial
period. Let us suppose, that the wave is defined by stars at a given
epicyclic phase, e.g., at minimum radius (point of greatest radial
compression). In the case of the leading one-arm this means that the wave
pattern merely has to travel (counter to the rotation) through an angle of
about 105° to meet the star again at minimum radius, and thus, close the
orbit in the wave frame. The wave must be leading because stars at larger
radii take longer to traverse their 255° of azimuth, by which time the
inner wave has traveled more than 105° (i.e., farther
"backwards").