


This chapter is about the evolution in systems where the interaction does not end with a single impulsive collision. Specifically, we will consider morphologies that are either produced in multiple collisions, or formed on comparable timescales. We also begin the discussion of several long term dynamical processes like dynamical friction and collisionally induced bars.
5.1 Dynamical Friction - Bringing It Back.
Dissipative collective effects are an important part of the reason why galaxy mergers are common, and a key process in galaxy evolution. Dynamical friction is the primary dissipative effect. In astrophysics this process was discovered by Chandrasekhar (1942, 1943), and completely developed for the case of a massive object moving through an infinite, homogeneous sea of low mass objects with which it interacts gravitationally. The basic idea is that the massive object pulls the low mass objects towards itself as it moves through them, generating an overdense wake. The gravitational pull of the wake in turn decelerates the massive object, much like a frictional force. Chandrasekhar derived a simple analytic formula for this force; a brief version can be found in BT (sec. 7.1). His first application was to stars in star clusters that randomly acquired speeds greater than the escape speed from the cluster. These stars might be retained, and the cluster's life prolonged, as a result of dynamical friction. Another application was to star clusters moving through a background of "field" stars in a galaxy.
Chandrasekhar's formula was not applied to colliding galaxies until the 1970s. First, it was recognized as the cause of sinking satellites. In terms of the basic theory this is the same problem as the star cluster in the galaxy, but with a small satellite galaxy instead (see the review of Ostriker 1977). Then, Toomre (1977) argued for its operation in collisions between two galaxies in order to explain the results of early N-body simulations. While the sinking satellite studies showed it was a mechanism of satellite accretion, Toomre suggested it was the agent of what are now called major mergers.
This stimulated renewed interest in the process, and in Chandrasekhar's formula in particular. There are several problems in the application of this formula, however (see e.g., Tremaine and Weinberg 1984, Séquin and Dupraz 1996). The first is that in its derivation, the force integration over all the infinite sea of low mass "stars" diverges unless minimum and maximum impact parameters are selected. The ratio of these impact parameters appears in the so-called Coulomb logarithm term (from plasma physics) in the formula. This means the formula depends on how these terms are selected, and is essentially phenomenogical. On the other hand, the quantitative dependence on the parameters in this term is weak. Moreover, there is a natural choice for the values of the minimum and maximum parameters as the satellite and primary galaxy sizes.
The second difficulty is that the derivation suggests no way to modify or generalize the assumption of an infinite, homogeneous background, e.g., to a spherical galaxy with a declining density profile. The third difficulty is that even though the friction is the result of a long range force, an obvious generalization is to identify the background density term with the local density. However, across a sharp density edge, this would give a discontinuous change in the friction. Finally, Tremaine and Weinberg noted a surprising fourth problem, the formula is simply wrong in some cases:
Kalnajs (1972) has computed the dynamical friction force in an artificial but exactly soluble galaxy model consisting of a uniformly rotating sheet of stars. This is the only analytic model in which the collective effects due to the self-gravity of the disc stars can be included. Kalnajs finds that collective effects modify the disc response so that there is no dynamical friction. (Tremaine & Weinberg 1984, p. 730).
As more N-body studies were published in the early 1980s it became increasingly clear that collective (feedback) responses were as important in determining the friction as the summed effects of individual star-satellite interactions (e.g., White 1983).
The paper of Tremaine and Weinberg (1984, henceforth TW) presented a new analytic approach to dynamical friction which was capable of capturing global responses, and overcame many of these difficulties. Chandrasekhar's formula derives from direct integrations over all two-body (star-satellite) interactions. TW's approach was a perturbation analysis of the Poisson and Hamilton equations for a star moving in the galaxy potential, with the additional perturbing potential due to the satellite. Only after the stellar accelerations were computed in the perturbation approximation were the integrations over all stars carried out. The two approaches were shown to yield the same result for the infinite, homogeneous medium, but the perturbation analysis can be carried out in the spherically symmetric case as well. Specifically, TW applied the analysis to the case where the perturbing potential was a weak bar component, and derived the "LBK torque formula" (after Lynden-Bell & Kalnajs 1972) for the "frictional" torque exerted on the bar. Though this formula and the procedure from which it is derived are very complex, no logarithmic divergences result from this approach.
At the conclusion of this calculation, TW note two important effects that were not included: strong or resonant interactions, and the continuous change in the motion of the bar or satellite. The resonances are generally transient, and TW were able to calculate their effects in a representative case. They found that the resonant interactions dominate the acceleration, but that in the case of fast resonances the LBK formula is correct. In the case of slow resonances, reversible torques operate, and the LBK and Chandrasekhar formulae are not applicable. Resonant interactions also provide a way for friction to operate even when the satellite is located outside the galaxy. In the end TW provide theoretical resolutions to all the problems of the Chandrasekhar formula, and equally importantly, clarify when it is applicable.
Weinberg (1986, 1989) followed up this work with examples of explicit perturbation calcutions of the wake structure and frictional drag on satellites in circular orbit about spherically symmetric primary galaxies. The second paper, in particular, calculated the self-gravitational response of the galaxy to the satellite wake in a specific case. Weinberg found that in this case the orbital decay time was increased by a factor of 2-3, primarily due to the barycentric motion. This motion is a global effect, which induces a counterwake in the primary galaxy. This effect provides a clear illustration of why the approximation that dynamical friction cannot depend only on the local density within a rigid galaxy.
Séquin and Dupraz (1993, 1994, 1996) have studied dynamical friction in the case of head-on galaxy collisions, using both N-body simulations and an appropriately taylored version of the Weinberg formalism. The 1993 reference presents a summary and comparison between the analytic and numerical results. Again global effects, like the tidal distortion of both galaxies are found to be important. Moreover, radial encounters "are both qualitatively and quantitatively different" from near circular encounters. The transient response in the radial case is one reason. Secondly, in the spherical harmonic expansion of the density and potential of the primary galaxy, the monopole and dipole terms were found to be more important in the radial case (see the 1993 paper). In fact, these authors find that in the radial case, almost all of the dynamical friction is due to the first few harmonic terms.
Very recently, another perturbative approach, based on "linear response theory" applied to the disturbing forces has been developed by Colpi and Pallavicini (1998, and Colpi 1998), and Nelson and Tremaine (1997). When applied to the satellite accretion problems this method has comparable successes compared to the other recent approaches. Moreover, this method makes clear the connection between this problem and the fluctuation-dissipation theorem of statistical physics.
In sum, a much more complete understanding of the phenomena of dynamical friction, a key ingredient in the merger process has been achieved in the last two decades. However, it has come with a high price in terms of theoretical and analytical complexity. The latter is obvious to the reader of the references above. By theoretical complexity I mean that many different cases must be considered separately, and we cannot rely on a single, simple formula. However, there is a silver lining to this dark cloud - the new, more complex theory is intimately connected to, and provides insights into, the theories of tidal disruption and bar evolution.
5.2. Simulational Examples of Dynamical Friction
The theory described in the previous section, and in fact our understanding of all intermediate timescale processes, are hard to check observationally. The tidal morphologies are usually messy and complex after multiple encounters, and so, it is very difficult to decipher their specific histories to the degree possible for those produced by single collisions. On the other hand, the systems have not yet settled down to quasi-equilibrium states like older merger remnants. Thus, the comparison of theory and numerical experimentation is very important for understanding dynamical processes operating on this timescale, while observational comparisons play a smaller role at present.
Aside from merger simulations, which we defer to the next chapter, the simulational studies relevant to dynamical friction theory are concentrated in two areas - the sinking satellite problem, and its orthogonal counterpart, which we might call the "bobbing" satellite. The former are generally assumed to be in circular orbits initially, and in the latter case the satellites are on nearly radial orbits. Let us consider the "sinkers" first.
5.2.1. Sinking Satellites (IDe+/-)
Most of the sinking satellite studies have concentrated on one of two particular cases, either the satellite is assumed to be in a circular orbit around a spheroidal (or spherical) primary, or if the primary is a disk galaxy, the orbital plane of the satellite is assumed to have a small inclination to that of the primary. For brevity, I'll refer to the latter case as the planar case. A number of N-body studies were carried out in the 1980s, as were comparisons between them and the analytic works, notably the work of Hernquist and Weinberg (1989). This literature was succintly reviewed by Athanassoula (1990). In fact, this seems to have been an especially good moment for a review, since several issues had recently been resolved. In the spheroidal case, a controversy in the literature over the role of self-gravity was settled, in part by the realization of the importance the motion of the primary galaxy about the center of mass. More generally, the analytic work of Weinberg discussed above demonstrated the global response of the interacting system. Hernquist and Weinberg's comparisons of analytic models and simulations showed generally good agreement, particularly on the result that sinking times are longer (e.g., a few times 109 yr.) than predicted by the Chandrasekhar formula. There was excellent agreement in limiting cases, and discrepancies could be understood as the result of nonlinear effects not adequately included in the analytic model.
In the planar case, the realization of the role of resonance orbits (a la Tremaine and Weinberg), and how their interactions can work in the opposite sense of standard friction, was an important breakthrough. Among the important results cited by Athanassoula are the more rapid decay of heavy satellites (a clear result of global effects), and the slower sinking of satellites in retrograde and highly inclined orbits as compared to those in prograde planar orbits (e.g., about 109 yr. in the recent prograde model of Walker et al. 1996). Since most of these effects were considered in the previous section, we will not discuss them further. However, before leaving the sinking satellites, we will briefly note two related effects.
The first is the Holmberg (1969) effect, which is the tendency he found, in a modest sample (58) of edge-on disk galaxies, for small companions to be found more frequently near the poles of the disk galaxy than near the disk plane. Quinn and Goodman (1986) drew the connection with our topic by hypothesizing that the effect was the result of more rapid sinking rates for satellites near the disk plane (especially the prograde population). Unfortunately, their simulations did not reveal a large enough difference between polar and planar orbits to account for Holmberg's result. This prompted a re-examination of the effect itself, by means of several catalog searches, but because of the small sample sizes a statistically significant result could not be obtained.
Zaritsky et al. (1993b) have looked at the subject again with a "homogeneous" sample of nearly 100 late-type spirals. They found evidence for a "weak" Holmberg effect for satellites within a (projected) radius of about 50 kpc., with an isotropic satellite distribution at larger radii. Although the satellite numbers are still too small for reliable conclusions, a weak result would seem more in accord with the theory and simulations. These authors also reported another, Holmberg-like effect, - "satellites on prograde orbits tend to be brighter than those on retrograde orbits."
The second effect of planar sinking satellites is disk thickening via dynamical heating as the satellite settles through the disk. The basic effect is straightforward - as long as the satellite is not completely disrupted it serves as a scattering center for individual disk stars. This effect was also studied by Quinn and Goodman. They pointed out that, while the thickening effect could potentially be very large based on the energy available, in fact, it was modest in their simulations. Instead they found that most of the dynamical heating occured in the plane, i.e., the radial velocity dispersion of disk stars increased much more than the vertical dispersion. Yet the effect was significant, and a number of studies in the last decade have confirmed and elaborated the result.
Quinn and Goodman used a restricted N-body method in their simulations, but the subsequent study of Quinn, Hernquist and Fullagar (1993) was fully self-consistent with three components: a primary halo and disk, and a single component satellite. The later paper also considered higher inclination orbits, where the companion was found to sink into the plane faster than it sank in radius. The satellites on higher inclination orbits increased the vertical velocity dispersion as much as the other directions in the outer disk. The most ambitious simulational study to date is that of Walker, Mihos and Hernquist (1996), using large-scale N-body simulations of three components as in Quinn et al. With 500,000 particles they were able to use a relatively small companion (10% of the primary mass), but still have adequate particle resolution of all components. In their fiducial model a companion placed on a 30° inclination orbit reached the center after 1.0 Gyr., retaining 45% of its mass. The primary disk was thickened by 60%, and all velocity dispersions increased by comparable amounts. Figure 16 shows the interesting structure that developed through the course of this "minor merger". Another recent N-body study, by Huang and Carlberg (1997), focusses on the fate of low-density sinkers, and finds such companions can be destroyed without contributing significantly to disk thickening.
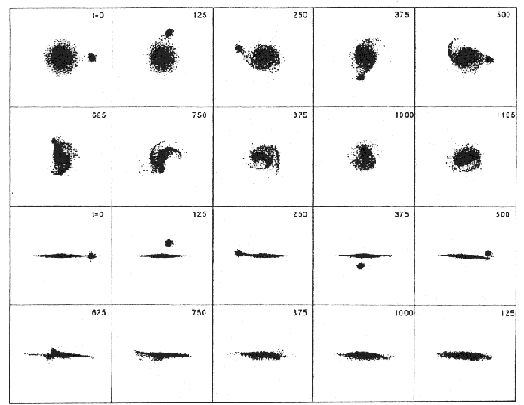
|
Figure 16. Sequence of face-on and edge-on views of a numerical N-body simulation of a minor merger from Walker et al. (1996). Note the waves that develop in the face-on view, and the disk thickening in the edge-on view. (Time indicated in units of about 125 million years for typical galaxy scales.) |
On the observational side, Reshetnikov and Combes (1996, 1997) have recently compared a sample of 24 edge-on interacting disk galaxies to a control sample with 7 objects. They find that the interacting galaxies have a much lower ratio of disk radius to disk thickness, which they attribute to the combined effects of disk thickening and radial truncation. Further studies with larger samples would be very interesting.
5.2.2 Bobbing Satellites (IXx0)
Satellites sinking on radial orbits, the "bobbing" satellites, have been most studied as means to form shell galaxies, in which case the satellite is usually assumed to have a very low mass, and be readily disrupted. Radial orbits have also been used in early studies of mergers between nearly equal mass galaxies. Both of these case are discussed in the next chapter. In their recent papers on dynamical friction Séquin and Dupraz (1993, 1994, 1996) present N-body simulations of the case of head-on collisions with intermediate mass companions (5-10% of the primary mass). The basic result is that satellites on parabolic orbits do not bob for long. They are generally merged within a few crossings, with the exception that "diffuse" satellites are highly disrupted, as discussed above. There are some interesting differences relative to the circular case. The most important of these is the fact that the radial case is much more time-dependent; dynamical friction occurs primarily in discrete jumps during each interpenetration. This is because the transient response of both galaxies enhances the friction nonlinearly. E.g., according to the authors, "between radial and circular orbits the relative contribution of the monopolar term (contraction during the collision) to the total drag undergone by the satellite decreases from dominant to zero." Clearly, the Chandrasekhar formula misses the dominant effect in this case.
As noted in section 4.2, Séquin and Dupraz's simulations include only single component galaxies. The question of what happens to the disk in multiple radial collisions has not yet been well studied, but the indications are that it is a very interesting area. First of all, the simulations of Taniguchi and Noguchi (1991) show that if the relative orbit lies in the plane of the primary disk the consequences can be incredibly violent, producing a highly distorted "wing" galaxy.
On the other hand, Lotan has studied the case where the relative orbit is near the symmetry axis of the primary disk, i.e., the ring galaxy case, but with multiple collisions (see Lotan-Luban 1990 and discussion in AS96). She used restricted three-body simulations with the inclusion of the Chandrasekhar formula for dynamical friction. Thus, the results cannot be regarded as accurate, but they reveal a fascinating effect whose existence should not depend on the details of the friction. If the companion returns while ring waves are still propagating through the disk, it imparts a new impulsive radial perturbation onto the pre-existing pattern of radial phase oscillations. The result is like wave interference, with enhanced wave amplitudes at some radii, and near cancellation at others. Qualitatively, it would seem that the strong impulsive friction found by Séquin and Dupraz would speed the return and enhance this effect.
In conclusion, simulation results and the current analytic theory of dynamical friction are in good accord. Because of the complexity of the latter, simulations can still produce surprises. The history of the Holmberg effect illustrates just how difficult comparison to observation can be when subtle dynamical effects are involved.
This topic is closely related to the previous one, since both deal with an intermediate time effect that draws galaxies together. Galaxy and galaxy group halos play a key role in accelerating the pace of successive collisions and mergers. Actually, there are several specific effects involved here. The first is just the fact that since galaxies have massive halos, they are much more likely to be gravitationally bound at a given separation and relative velocity than in the absence of such halos.
There is evidence that galaxies in small groups are often contained in
an extensive dark halo. For example,
Ramella, Geller and
Huchra (1989),
in a
study of groups in the Center for Astrophysics redshift survey, found median
mass-to-light (M/L) ratios of about 180 in solar units, which is much larger
than typical values of individual galaxies. They also found a median halo
scale size of about 500 kpc. On the other hand, the M/L ratios in Hickson
compact galaxy groups are smaller, though still not small (about 50, according
to Hickson et al. 1992).
The collisional ring galaxy VII Zw 466 is part of a
small group, which was recently estimated to have M/L
 70
(Appleton, Charmandaris,
and Struck 1996).
70
(Appleton, Charmandaris,
and Struck 1996).
Granted this result, we would expect that the dynamical friction on a companion from this halo is a major effect, but this turns out to be an oversimplification. The review of Barnes and Hernquist (1992a, henceforth BH92a) provides a good brief summary, as follows.
Roughly speaking, a pair of spherical, interpenetrating dark halos interact as if they were single-component systems: the orbital angular momentum of the two halos is transferred to internal degrees of freedom, imparting spin and creating broad tails. ...embedded disks and/or bulges, are not much braked by the tidal forces retarding the dark matter; instead, these components lose orbital angular momentum mostly by interacting with their own surrounding halos, once the latter have been decelerated.
These results are basically confirmed by recent N-body simulations of mergers in galaxy groups. E.g., Governato, Tozzi, and Cavaliere (1996) also find that friction operates first on halos. They also note the interesting result that galaxies falling into a group can be stripped of their halos, which can delay merger with the group galaxies. The multiple merger simulations of Weil and Hernquist (1996) also show the basic phenomenon of prompt halo merger. Their Figure 3 clearly illustrates the dynamical heating of the halo in the merger process.
In sum, these results inspire a much more optimistic view of the probability of collisions and mergers, compared to the general opinion when Toomre proposed it in the 1970s. Now, since most galaxies are born in groups, collisions and mergers appear to be almost inevitable on a group free-fall timescale.
5.4. Tidal Stretching: Tails and Antennae (IXd+)
Long tidal tails, jets, and plumes that stretch out to several galaxy diameters or more, are some of the most spectacular structures formed in galaxy collisions. The Arp atlas contains a number of famous examples, including well-known systems like the "Mice", the "Antennae", and the "Atoms for Peace". Table 1 of Schweizer (1983) contains a list of nearly two dozen. Melnick and Mirabel (1990) presented a number of additional southern examples, including the "Superantennae" with a 350 kpc. long tail (Mirabel, Lutz, and Maza 1991)! Figure 17 shows Appleton et al.'s HI map of the Leo plume, drawn out from the galaxy NGC 3628. Because of its proximity, this structure stretches an incredible 40° across the sky.
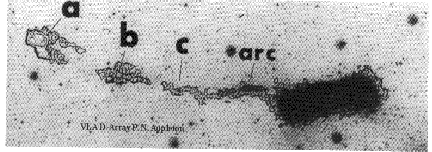
|
Figure 17. The giant tidal plume extending out 40 degrees from the galaxy NGC 3628 in Leo. The angular size of this plume is very large because it is relatively nearby. It is otherwise a representative tidal plume. (Unpublished image courtesy P. N. Appleton.) |
We have already covered the mechanisms responsible for producing these tails: it is simply tidal stretching and torques, and the slinging of outer disk components that result from the motion of the potential center. TT first demonstrated that these mechanisms can produce such long structures, specifically, in their models of the Antennae and the Mice systems. The result has been verified in more recent years with N-body simulations, e.g., by Barnes and Hernquist (1992b), Elmegreen, Kaufman, and Thomasson (1993) and Mihos et al. (1993).
Since tails are formed in essentially the same way as the "tidal
transients", the reader might wonder why they are discussed here, rather
than in chapter 3? The answer is that the kinematic timescales of such large
structures are long. For example, consider the free-fall timescale,


 -1/2
-1/2
 (r3 / M(r))1/2. Within a dark matter halo M(r)
(r3 / M(r))1/2. Within a dark matter halo M(r)
 r,
so
r,
so 
 r. Thus, at the end of a 100
Mpc long
tail, this timescale is of the order of a few Gyr., or longer if the halo does
not extend that far. This helps understand the result of
Barnes' (1988)
N-body simulations that tails are still evident after the galaxies that
produced them have merged. Thus, the presence of tails can reveal the
collisional history of a galaxy when other traces have disappeared in the more
settled central regions.
r. Thus, at the end of a 100
Mpc long
tail, this timescale is of the order of a few Gyr., or longer if the halo does
not extend that far. This helps understand the result of
Barnes' (1988)
N-body simulations that tails are still evident after the galaxies that
produced them have merged. Thus, the presence of tails can reveal the
collisional history of a galaxy when other traces have disappeared in the more
settled central regions.
The specific topic of the formation of star clusters or dwarf galaxies in tidal tails deserves further discussion. The idea that clusters or dwarf galaxies can be formed in bridges and tails, and subsequently, with the dissolution of the tail, be freed to orbit the galaxy dates to Zwicky (1956, also 1959). It seems likely that the idea was viewed as very novel at the time. Schweizer's (1978) discovery of the young cluster at the end of one of the "Antennae" made it much more plausible by providing a good example. Mirabel et al. (1992) studied this object further, and concluded that it was indeed a young, low-surface-brightness dwarf irregular galaxy.
Since then a number of other possible examples have been discovered, including the Superantennae which has young star clusters distributed along its great length. Arp 105 may have formed two dwarfs in its collision(s), a blue compact one to the south, and a Magellanic irregular in the north at the end of a long plume (Duc and Mirabel 1994). The interacting cluster galaxy NGC 5291 is another example (Malphrus, Simpson, Gottesman, and Hawarden 1997, Duc and Mirabel 1997, 1998). A number of other examples have been studied recently (Hibbard and Van Gorkom 1996, Duc et al. 1998, Deeg et al. 1998). Hunsberger, Charlton, and Zaritsky (1996) found 47 candidate dwarf galaxies associated with tidal tails in a survey of 42 Hickson compact groups of galaxies. They estimate that as many as one half of the dwarf galaxies in compact groups may be "the product of interactions among giant parent galaxies." However, most of these objects have not been studied in detail, so we lack evidence that they have the detailed characteristics of dwarf galaxies, and specifically, are sufficiently strongly self-gravitating to become independent entities (see discussion in Schweizer 1998, and the models of Barnes 1998).
The phenomenon of star formation in tails is also of general interest because SF is unusual so far from the center of the parent galaxies. At first sight this seems mysterious - should not gas stretched out of a disk be less likely to form stars? However, there are several interesting effects that make it possible. The first, discussed above in section 4.1.3, is the tendency of bridges and tails produced by tidal torques to remain on a two-dimensional surface, rather than spreading into the third dimension. The second is that, as discussed explicitly by Wallin (1990), and as is apparent in early simulations, intersecting caustics and compression waves propagate along tidal spirals and tails. (This is true even when the tail itself is primarily a material wave.) These compressions may stimulate massive cloud formation and star formation. Furthermore, Elmegreen et al. (1993) have argued that because large velocity dispersions are found in these tidal structures, local gravitational instabilities assemble very large gas clouds. Both large clouds and large velocity dispersions were found in their N-body simulations, as was the tendency for an "extended gas pool" to accumulate at the end of the tidal arms.
Several of these phenomena can be understood as natural results of the basic fact that in these types of collision, the orbit shapes of the gas clouds in the outer disk are changed from nearly circular to primarily radial. The dispersion of radial phases generates the propagating caustic waves as described in chapter 3. The fact that there is an outermost excursion radius for the radial particle orbits accounts for pileups at the ends of tails. At other locations within the tail, particles are moving both radially inward and outward. It is reasonable to expect that collisional interactions between gas clouds moving in opposite directions may convert some of that motion into enhanced velocity dispersions.
Simulational studies of tail dynamics are advancing, but many of these conjectures await testing with higher resolution, gas dynamical models. Even without gas there are complications. For example, several recent studies have clarified the role of halo structure in determining the morphology of stellar tails, and how this dependence might be exploited to probe halos (Dubinski, Mihos, & Hernquist 1996, Mihos, Dubinski, and Hernquist 1998, and references therein). In any case, this is a very interesting environment for studying details of the gravitational instability, both numerically and observationally, if a wide range of length scales could be resolved.
The story of shell ellipticals is dramatic. Their surprising discovery initiated a decade of intense activity, after which the phenomenon is almost taken for granted as another merger diagnostic, see Figure 18. Presently, work on a variety of outstanding questions continues more quietly. Malin's (1979) initial discovery of huge, sharp, edge or shell-like structures wrapped around the "normal" elliptical M89 was all the more surprising because it was the result of a little known photographic technique, called unsharp masking (see Malin 1993). Malin and Carter (1980, 1983) soon presented more examples, and then a catalog. Schweizer (1980, 1983) realized that shells could be produced in mergers, and produced a list of merger candidates with "ripples", his preferred term. For detailed descriptions of shell morphologies and systematics see the review of Prieur (1990), and references therein.

|
Figure 18. The prototypical shell galaxy NGC 3923. Several sharp shell edges are visible in this negative image, even without special processing. (Digital Sky Survey image courtesy of AURA/STScI.) |
At the same time Quinn (1982, 1983) and Toomre (as quoted in Schweizer 1983) produced the first numerical simulations. These works showed that it was possible to produce sharp-edged features from the disruption of a small, disk galaxy companion via multiple crossings of a large elliptical primary. Quinn (1984) presented several simulations and describing in detail how the "phase wrapping of the dynamically cold disk material" produced the shells. The basic idea of this process is well illustrated by his Figure 5, reproduced here as Figure 19. (The figure shows that again, as in section 3, we are dealing with radial caustics.) Quinn also found that nearly radial collisions did the best job of reproducing observed interleaved shell morphologies. High angular momentum collisions produced "spatially wrapped" shells whose appearance depended strongly on viewing angle, and which crossed and overlapped in ways that the shell ellipticals did not.
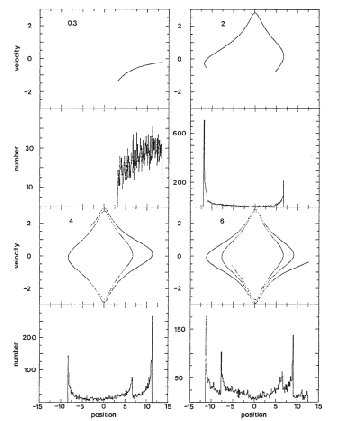
|
Figure 19. Evolution of the phase and configuration space distribution of a set of test particles falling from rest into a rigid (isochrone) galaxy potential, representing the formation of a shell galaxy (from Quinn 1984). The time in units of the radial period of the most tightly bound particles is shown in the phase plots. Positions are given in units of the potential scale length. |
This suggested that shells were only produced in a rather narrow class of collisions. Since observations suggested that shells were not uncommon around ellipticals, this appeared to be a weakness of the collisional theory. Alternate models had been proposed, and the interested reader can find a summary of them in the review of Prieur (1990). However, the situation didn't lead to wider acceptance of these alternatives, but rather to a broader investigation of the collisional model, and a number of new simulational studies.
In several papers, Hernquist and Quinn described, e.g., how shell structure depended on the density profiles and shapes of dark matter halos (1987, 1989). These topics were also treated by Dupraz and Combes (1986). There was agreement that shells could be produced in a variety of different potentials. Thus, Hernquist and Quinn (1989) concluded that "it will not be possible to unambiguously determine the mass distribution of the primary galaxy from observations of the morphology of shell systems alone," ending an earlier hope. More positively, both Dupraz and Combes (1986), and Hernquist and Quinn (1988) generalized the initial studies by finding that shell formation was possible in nonradial encounters, and with early type (elliptical) companions. This removed the major problem of the merger theory, that it required fine-tuning. Hernquist and Quinn (1989) also discovered that the curious X-structures observed in some galaxies, were produced in some of their simulations, and so could be the result of accretion in some cases (see BH92a, and for a recent view, Mihos et al. 1995).
These simulations were of the restricted three-body, or similar test particle, types, and as Dupraz and Combes pointed out, they did not resolve one difficult problem. This is the huge range of radii, up to a factor of 30 in the extreme case of NGC 3923 (see Figs. 20, 18). Dupraz and Combes conjectured that dynamical friction would play an important role in producing such systems, and thus, self-consistent N-body simulations woudl be needed. At the turn of the decade, several papers showed that shells, in fact, could be produced in self-consistent N-body simulations (e.g., Barnes 1989, Salmon, Quinn, and Warren 1990).
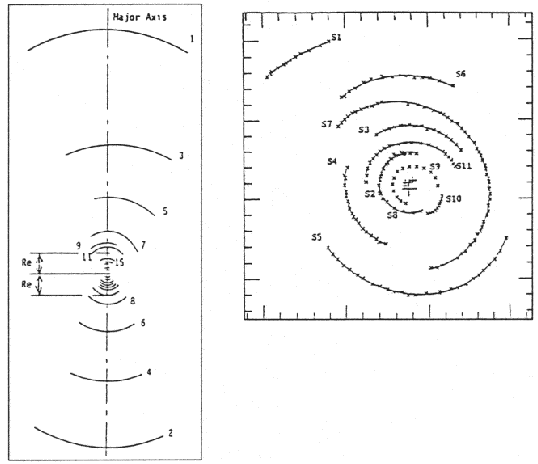
|
Figure 20. Prieur's shell galaxy type classification is illustrated by schematics of two systems. NGC 3923 on the left is an aligned system (type 1), and 0422-476 on the right is all-round, type 2 system (from Prieur 1990) |
Heisler and White (1990) made a detailed study of the radial structure with simulations that included a self-consistent treatment of the companion (in a low order, spherical harmonic approximation), and a rigid potential for the primary. They found that "there is a substantial transfer of energy in the various parts of the satellite" in the disruption process. This is the key that allows some stars to be thrown out to great distances, while other stars are left tightly bound to the primary center. Moreover, "the most extensive shell systems are formed for satellites of relatively high mass with mean densities similar to that of the primary." Heisler and White did not quite succeed in getting as large a range of shell radii as observed, but they (also) speculated that the inclusion of dynamical friction might complete the job. In light of the impulsive dynamical friction found by Séquin and Dupraz (1996, and see sections 5.1, 5.2 above), in radial encounters with modest mass companions, this seems highly probable. The large-scale N-body simulation of Salmon et al. (1990) also showed a large range of shell radii, suggesting this is correct.
Another possible solution is that the deep shells might, in fact, be internal ripples in a small inner disk in the elliptical (Thomson and Wright 1990, also see discussion in BH92a). However, the continuity of shell intensities and colors with radius in NGC 3923 (Pence 1986, Fort et al. 1986), argues against separate origins for some shells (although these works could not treat the deepest shells). Yet internal oscillations may be responsible for some of the less regularly rippled systems. This was shown by the models of Wallin and Struck-Marcell (1988) of direct, off-center collisions, similar to those that make ring galaxies, but with gas-poor primary disks. At long times, compared to the propagation time of an individual ring wave, the asymmetric ringing produces shell-like features. These ripples are not as aligned or well-ordered as in classical shell systems like NGC 3923, but more like the Type 2 systems of Prieur (1990, see Fig. 20). They are, however, phase and not material features.
These models were inspired by observations of Arp 227, whose primary is a rippled S0, which has not merged with its companion (Schombert and Wallin 1987). However, a ring-ripple interpretation of this system is based in part on the belief that the colors of the ripples and primary are similar, but McGaugh and Bothun (1990) suggest that with proper subtraction of background starlight the shells are somewhat bluer. This might suggest that they were accreted. Recent work on Arp 10, a ring galaxy with outer ripples indicates it may be a better ring-ripple example, whose companion is almost merged (Charmandaris, Appleton and Marston 1993, Charmandaris and Appleton 1996).
The shell galaxy story is largely based on optical observations of the stars, but what about the gas? We expect that multiple, near radial collisions, which disrupt the stellar component, and presumably the halo, of the companion to have a similarly catastrophic effect on the gas component. In the only substantial simulation study to date, Weil and Hernquist (1993) showed that this is indeed the case. Moreover, because of dissipation in the gas, it rapidly became separated from the stars. While the stars continued their radial, shell-making oscillations, the gas settled into a compact inner ring or annulus. The cleaness of this result may, in part, be due to the adopted approximation that the companion halo vanishes at closest approach in the first collision, i.e., it is assumed to be of such low mass that it is completely disrupted. Nonetheless, the result is both reasonable, and as the authors point out, supported by observations of compact disks in shell ellipticals.
Yet the recent HI mapping studies of van Gorkom (e.g., Hibbard et al. 1994, Schiminovich et al. 1995) and collaborators have shown that gas shells, ripples or streamers can also be found in interacting or merged systems. This is not to suggest a contradiction with the models or the theory. The gas structures resemble the messier ripple systems (Prieur Type 2), with usually no more than a few features per system. There are no (Type 1) examples with numerous, interleaved gas shells. The implication is that they are spatially wrapped shells produced in high angular momentum collisions. Another possibility found by the author in unpublished simulations is that detached streamers can be formed in off-center collisions involving two gas disks, when there is partial overlap at impact.
Very recently, Kojima and Noguchi (1997) have carried out N-body simulations of the merger of a gas-rich spiral and an elliptical galaxy, using sticky particle hydrodynamics. The stars from the disk galaxy make shells, the gas is dispersed over a wider part of the volume containing the shells, and star formation is terminated by the gas dispersal. New simulations of Charmandaris and Combes (1998, private communication) emphasize that a large part of the morphological differences between the gas and star shells produced in a given system are the result of the much greater radius of the initial gas disk, and subsequent collisional kinematics. These tentative results suggest that this will be an exciting area for continuing work.
The collisionally induced formation of stellar bars is one of the most important intermediate timescale process in terms of its long-term consequences. Hints of the importance of this process appeared early, but since it is a collective effect, and requires fully self-consistent (N-body) modeling, it took longer to realize its full ramifications. For example, Lynden-Bell (1979, also 1993 and Earn and Lynden-Bell 1996 for updated pedagogical discussions) demonstrated that an oval perturbation can readily induce bar formation in the rising rotation curve region of a galactic disk, because of the nearly solid-body kinematics of such regions. The work of Toomre and Zang discussed above (Sec. 3.5) showed the Swing Amplification process could also lead to bar formation. However, the dramatic rapidity of bar formation in prograde collisions, and the effectiveness of such bars in funneling gas into the central regions was first, clearly demonstrated in Noguchi's simulations (1987, 1988, also see his 1990 review, and the reviews of Athanassoula 1994 & Combes 1994).
5.6.1. Collisional Bar Formation
The tidal forces in all non-central collisions naturally produce oval distortions, but as kinematic features they would be expected to phase mix and disappear relatively quickly. The prograde planar interactions studied by Noguchi (1987) produce a relatively strong and synchronous perturbation, as discussed above in connection with tidal spirals. Noguchi's models had two components, a halo and a stellar disk. The mass was initially distributed such that there was a significant rising rotation curve region, where Lynden-Bell's work would suggest induced bar formation was likely. The size of this region, and the disk-to-halo mass ratio were varied. The only models that didn't form bars were ones with small disk masses or very small rising rotation curve regions. In most cases the perturbation was strong enough, and the disk sufficiently susceptible, that self-gravity was able to organize a long-lived bar. Similar but weaker, results were found by Byrd et al (1986), whose flat rotation curve disk was less susceptible to bar-making.
Noguchi (1987) also found a number of interesting trends in his models. Firstly, bars formed more rapidly, and rotated faster, as the disk to halo mass was increased. Secondly, the same results were obtained when the halo was made more centrally concentrated. These results are not too surprising since if the central mass is increased, then the fundamental gravitational timescale is decreased. Thirdly, the bars formed more rapidly and were much longer when the companion galaxy mass was increased.
While these trends are very interesting in their own right, but the general result is that bars should be even more common in interacting galaxies than in isolated disk galaxies. This provides a mechanism for understanding analogous observational results. For example, Elmegreen and Elmegreen (1982) found that fraction of barred galaxies was 81% in binary systems, as compared to 63% for isolated galaxies. In a sample of 48 paired galaxies, Schweizer (1986) found a higher percentage of systems containing at least one barred galaxy among those systems with two disk galaxies, as compared to systems with one disk and on spheroidal galaxy. This last result provides some indirect evidence for the mechanism of bar formation induced by prograde interactions of disk galaxies.
However, Noguchi's (1987, 1988) results had two significant limitations: the models were two dimensional and the perturbing companion masses were greater than or equal to that of the target galaxy. One might worry if collisionally induced bar formation would be weakened if stars could be scattered into the third dimension, or if a very massive perturber was required to induce bar formation in a galaxy that was stable against the bar instability before the interaction. (See BT sec 6.3, 6.5 for a discussion of bar formation in isolated galaxies. The work of Gerin, Combes and Athanassoula (1990), included three dimensional simulations with 50% mass companions, and thus, easied both limitations. This work both supported and extended Noguchi's results. These three dimensional simulations had very modest numerical resolution by current standards. However, the basic result has been reproduced in many subsequent simulational studies, and the idea of collisionally induced bar formation is now a commonplace.
5.6.2. Effects of Induced Bars
Before Noguchi's collisional models, studies of bars in isolated galaxies had shown the profound effects they can have on disk structure, including: dynamical heating of the stellar disk, driving of spiral waves (outside the region containing the bar), and inducing the radial flow of gas (see the reviews of Athanassoula 1994, 1996b and Combes 1994). The latter is the most important effect in the case of collisionally induced bars because, as Noguchi (1987) demonstrated, it is a means of funneling large amounts of gas into the central regions. This gas can, in turn, fuel nuclear starbursts and active galactic nuclei, which are commonly found in collisional systems.
The simulations of Noguchi and others have left little doubt about the effectiveness of this mass transfer process when a bar is present (e.g., Noguchi 1988, 1990, Barnes and Hernquist 1991, Mihos and Hernquist, 1996). The question is rather, what fraction of central SF and nuclear activity in collisional galaxies is mediated by bars. Noguchi suggested that this might be the primary mechanism responsible for the high frequency of such activity in interacting galaxies. He specifically argued that this mechanism was much more efficient at moving gas to the center than tidally induced spiral waves. Recently, Mihos (1994) has presented simulation results indicating that "under a wider range of interaction scenarios" the bar mediated process is more effective in inducing nuclear activity than another competing process - mass transfer between galaxies. Of course, the latter process, discussed above, is generally much more transient. Thus, with the caveat that mergers, in which time-dependent torques and fluctuating gravitational fields persist for some time, can generate the most intense nuclear activity, Noguchi's conclusion has held up well.
It is worth emphasizing that these simulations all involve parabolic, and so, relatively impulsive collisions. Thus, the longer timescale of the central activity has little to do with the collision, whose main role is to trigger bar formation. The nature of the subsequent radial flows are essentially no different than those in isolated galaxies. The effects and evolution of galactic bars have been the object of intense study in recent years, and there is a large literature on it (see the proceedings edited by Sandquist and Lindblad 1996, and Buta, Crocker and Elmegreen 1996). This literature provides several results that are very relevant to the topic of sustained inflows.
The first is that recent observational studies confirm that bars do indeed enhance the global SFR in the central regions of galaxies containing them (see the review of Kennicutt 1994 and references therein, and more recently Huang et al. 1996). However, the effect is more complicated than originally thought. In fact, centrally enhanced SF is only found in about 1/3 - 1/2 of the barred galaxies, and there is no difference between the global SFRs of barred and unbarred galaxies. There is also great diversity in the morphology and distribution of star-forming regions in barred galaxies. Yet there do appear to be systematic trends, especially with Hubble type according to Phillips (1993, as quoted in Kennicutt 1994). Late-type barred galaxies (SBc and later) "show exponential bars, rising rotation curves, relatively weak rings and star formation enhancements in the bar." While barred early-types "contain flat stellar surface brightness profiles, flat rotation curves, strong rings, but no star formation in the bar region" (Kennicutt 1994). In the latter case, SF is found in the circumnuclear region (often in rings), and in a normal distribution outside the barred region. Huang et al.'s recent study of the infrared properties of a large sample of barred galaxies is generally in accord with these generalizations, and adds the suggestion that "availability of fuel" (HI gas) is especially important in the early types.
Recent theoretical and numerical models help us understand these observations. A fine summary is given in the review of Athanassoula (1994, also see Sellwood and Wilkinson 1993, Athanassoula 1996a, b, Noguchi 1996b). In the first place Athanassoula makes it clear that the models have a comparable degree of complexity. The location, degree, and strength of bar-driven shocks, as well as the presence of central rings or spirals, all show considerable variation as a function of galaxy structural parameters. A second point that is especially relevant to collisionally induced bars, is that "the inflow is high during or after violent events like the formation of the bar, and much less during quasi-steady slow evolution of the bar." Bar-driven circumnuclear activity should follow a similar history following a collision or merger.
Athanassoula also summarizes current thinking on another important question, even if there is gas inflow, how does this gas get down to the very small radii that characterize the SF regions and active nuclei? Overcoming the centrifugal barrier would be difficult in itself, but there are additional dynamical barriers. Specifically, simulations show that the presence of an inner Lindblad resonance (ILR, see section 3.5) is very effective at slowing inflow, and retaining gas in a ring at the radius of the resonance. Some, but not all, galaxies have mass distributions that allow these resonances.
Shlosman et al. (1989) suggested a clever way around these difficulties, the bars-within-bars scenario. The basic idea is that the driven inflow raises the central surface density, which triggers gravitational instability on a small scale relative to the original bar. On this scale the potential is modified, so an ILR can be removed (or changed to a corotation resonance), and gas can be funneled down to still smaller radii. The reality and efficiency of this process are supported both by self-consistent simulations and observational evidence for small scale bars within a few "barred" galaxies (e.g., Athanassoula 1994, Friedli 1996). In principle, this process can repeat itself, and a nested set of bars can form and funnel gas down to arbitrarily small radii, though there is as yet little evidence for many multi-level bars (see section 8.2).
In conclusion, studies of isolated barred galaxies do indeed provide much insight into the question of what effects result from collisionally induced bars. However, they do not help much with the lingering questions of what are the requirements for such bar formation? Specifically, what combinations of structural and collisional parameters are needed? Since relatively little of the parameter space has been studied, these questions remain quite open.
5.6.3. Longevity, Frequency and Other Matters
Investigations of a number of related questions have begun recently. The first of these questions concerns the longevity of bars. While N-body simulations have demonstrated that bars can be long-lived, they are also subject to instabilities that can dissolve them. Hasan and Norman (1990) described how a central mass concentration, like a massive black hole, generate stochastic regions in the orbital phase space. As the central mass is increased, these regions grow, in association with the development and outward movement of an ILR. Ultimately this leads to the dissolution of the bar. Pfenniger and Norman (1990) studied the case where the central mass grows as a result of the inflow of gas clouds on weakly dissipative orbits. This generalized the earlier work by including a realistic growth process in order to study the temporal development of the process. The basic results of the earlier study were confirmed, the diffusion of stars from the disk into the bulge as the bar dissolved was also described. The authors suggested that a large fraction of all bulges might have formed by this mechanism, on a timescale of about a few billion years. The observational evidence for this idea was subsequently reviewed by Kormendy 1993, with a generally favorable conclusion, though the uncertainties are large.
Later work with three dimensional simulations of accretion or the merging of a small satellite supported the earlier results and is described in the review of Pfenniger (1992) and Hasan, Pfenniger and Norman (1993). The case where the central concentration is a nuclear gas ring seems to be somewhat different than the central point mass, according to the paper of Heller and Shlosman (1996). A related instability, the buckling or firehose instability, was reviewed by Sellwood (1992), and simulations of how it generates "boxy" or "peanut" shaped bulges were presented by Combes et al. (1990). Similar structures are formed from this instability following the merger of a small companion in the recent simulations of Mihos et al. (1995).
Bar longevity is closely coupled to another important question, what is the relative fraction of induced vs. intrinisic bars? If bars are relatively short-lived compared to the age of the galaxies, then their high abundance suggests that they are constantly being regenerated, by collisions or other means. However, many of the barred galaxies may not have an ILR, and have relatively low inflow rates, and so may have much longer lives than those studied in the papers above.
Noguchi (1996a, b) has recently presented a unified picture which incorporates these ideas, and a number of others above, with the disk formation process. The latter connection is made by associating the inflow in isolated galaxies with the accretion process in the formation of the disk. Thence,
...we propose that late-type barred galaxies, the disks of which are considered to have formed by slow accretion of the halo gas, have intrinsic origin, whereas the bars in early-type galaxies, whose disks are likely to have grown quickly, have been formed in tidal interactions with other galaxies.
Numerical simulations...show that the bars created by tidal perturbations tend to have a relatively flat density profile...whereas spontaneous bars have a steeper profile. ...this numerical result can explain the observed dichotomy (between early and late-type barred galaxies) Noguchi (1996a).
These results are extended in Miwa and Noguchi (1998), who find that the disk resonance structure and pattern speedsin isolated, "intrinsic" barred models are different than those of bars produced in strong tidal interactions. The latter were found to rotate more slowly, in part, simply because they tend to be derived from more stable, lower mass initial disks. A caveat is that weak tidal perturbations were found to produce bars whose structure depends mostly on internal properties, and so, are more "intrinsic."
One of these complications is the final question for us to consider in this section, what effect do collisions have on pre-existing bars? It appears that this question was first addressed in the paper of Gerin, Combes, and Athanassoula (1990), who noted that a tidal interaction could transiently increase or decrease the strength and angular velocity (pattern speed) of a pre-existing bar, depending on the relative phase at closest approach. In several recent papers Athanassoula (1996a, b, Athanassoula, Puerari, and Bosma 1996) has reported the results of a much broader exploration of this question using self-consistent simulations. The main result is an enormous range of possible outcomes. Depending on the companion and orbital parameters the bar can be : essentially unaffected or destroyed, reformed in an off-center configuration, or turned into a lense, ring(s) or bulge on an intermediate timescale following collision or merger. Figure 21 shows an example from Athanassoula, Puerari, and Bosma (1996). The companion can meet a similar range of fates as discussed above, though the simulations reported in these papers had not yet covered a large range of companion parameters. E.g., all companion masses are less than 10% of the primary mass. These models are especially relevant for the case of multiple collisions (on the way to merger), where the first collision might generate a bar, whose fate would depend on details of the subsequent collisions. So we end this chapter on a note of great potential complexity.
The two most important processes that operate on intermediate timescales, but have long-term consequences, are dynamical friction and bar formation. Chandrasekhar's theory of dynamical friction operating on a massive object traveling through a uniform sea of low-mass stars played an extremely important role in helping to explain why galaxies merge. However, it is too idealized to account for the full range of "frictional" and collitive phenomena in galaxy collisions. That is, all fluctuation phenomena, and the collective effects of resonant orbit interactions. These are captured in the perturbative expansion formalism of Tremaine and Weinberg (1984), and the later papers cited above.
At the same time that this theory was being developed the importance of collision-induced bar formation became recognized, largely due to the results of numerical simulations. Bar formation requires both a relatively strong tidal disturbance, and a susceptible region in the center of the galaxy disk, though there are additional complications. Induced bars drive enhance star formation on intermediate timescales, and may contribute significantly to the net SF of the universe. Bars drive radial gas flows, and thereby feed active nuclei, either directly or indirectly.
Tidal tails and collisional shells, which can be drawn out to very large radii, are other examples of intermediate timescale effects.