6.2.4 Population Statistics for Radio Samples

The radio data are better suited than the X-ray data for testing the beaming hypothesis for BL Lac objects. One reason is that the radio sample of FR I galaxies is larger than the X-ray sample. In addition, the higher spatial resolution available with radio interferometry allows estimates of the ratio between beamed and unbeamed radio flux (Antonucci and Ulvestad 1985), thus adding an important constraint to the combination of the parameters and f (Appendix C).

The radio luminosity function of FR I radio galaxies was derived by Urry et al. (1991a) from the 2 Jy catalog (and converted to 5 GHz) and then extended to lower radio powers using the radio LF of elliptical galaxies of Franceschini et al. (1988). Here we choose not to include the low-luminosity radio ellipticals but restrict ourselves only to sources classified explicitly as FR Is (some of the lowest luminosity ellipticals could in fact have radio emission dominated by thermal emission rather than the nonthermal BL Lac nucleus; Phillips et al. 1986). Our results, however, are basically unchanged, since the beamed LF for BL Lacs at P₅ 5 x 10²⁵ W Hz^-1 (i.e., where it overlaps with the observed LF) is largely unaffected by the behavior of the FR I LF at such low powers. The new optical identifications (di Serego Alighieri et al. 1994b) and radio maps (Morganti et al. 1993) also have little effect on the FR I luminosity function; the fit to the new LF used here is consistent with the one in Urry et al. (1991a). The evolutionary properties of FR I radio galaxies are consistent with no evolution, with < V/V_max > = 0.42 ± 0.05.

We can compare our FR I luminosity function, derived from the 2 Jy sample (selected at 2.7 GHz), with that of de Ruiter et al. (1990), based on the B2 sample (selected at 408 MHz) plus nearby (z < 0.2) 3CR radio galaxies (selected at 178 MHz). Converting our FR I LF to H₀ = 100 km s^-1 Mpc^-1 and = 408 MHz (assuming _r = 0.7), we find excellent agreement from P₄₀₈ ~ 6 x 10²³ W Hz^-1 up to the break at P₄₀₈ ~ 3 x 10²⁵ W Hz^-1 (see Fig. 13 of de Ruiter et al. 1990). Above the break our LF is steeper, not surprisingly, since they did not exclude FR II sources. The two lowest luminosity bins in our LF (P₅ 2 x 10²³ W Hz^-1), lie a factor of 2-3 above the de Ruiter et al. LF. This disagreement is not surprising, as our two points are highly uncertain, with only one object in each bin. Also, the two objects, M82 ⁽¹⁶⁾ and M84, are nearby (z = 0.0014 and 0.0028, respectively) and so sample the local overdensity, whereas the B2 sample, being deeper than the 2 Jy, averages over a larger volume of space. (The equivalent flux limit of the B2 survey translated to 2.7 GHz with = 0.7 is 130 mJy.) In any case, excluding the first two bins does not alter our fitted beamed LF significantly.

Using a two-power-law approximation to our FR I luminosity function, we fitted a beamed LF to the observed LF for the 1 Jy BL Lacs. The latter was obtained as described in Stickel et al. (1991) with the addition of S5 0454+844, which had no redshift at the time. It is impossible to fit the data with a single Lorentz factor; instead, an acceptable fit to the LF and the observed R-values is obtained for Lorentz factors distributed in the range 5 _r 32. While the form of the distribution is not well constrained, it is weighted toward lower values; e.g., for a power law of the form N (_r) _r^G, the best-fit index is G ~ -4.

Figure 17 shows the excellent agreement between beamed (solid line) and observed (filled circles) radio luminosity functions for the 1 Jy sample of BL Lacs. The mean Lorentz factor, which is approximately independent of the exact shape of the distribution, is < _r > ~ 7, corresponding to a ratio between BL Lacs and FR Is of ~ 1:50, about an order of magnitude smaller than in the X-ray case (Sec. 6.2.3). The total number of BL Lacs is most sensitive to the lowest value of _r, while the maximum ratio of beamed to unbeamed flux is sensitive to the highest value. Our fitted model predicts that radio-selected BL Lacs are aligned within _c ~ 12° of the line of sight. The fitted beaming parameters for radio-selected BL Lacs are summarized in Table 3.

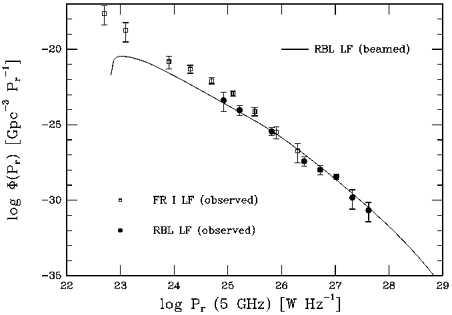
Figure 17. The local differential radio luminosity functions of radio-selected BL Lac objects (filled circles; Stickel et al. 1991) and FR I radio galaxies (open squares; Sec. 6.2.4), compared to the fitted beaming model (solid line; first set of RBL parameters in Table 3). Error bars correspond to 1 sigma Poisson errors (Gehrels 1986).

As we did for quasars, we can estimate a lower limit to the maximum Lorentz factor from the observed maximum and minimum values of R for BL Lacs and FR Is, respectively (Appendix C). OJ 287 is the most core-dominated BL Lac in the 2 Jy sample (and in the 1 Jy sample), excluding those cases where no extended emission has been detected, and Fornax A is the most lobe-dominated FR I. The corresponding values of R, K-corrected [Eq. (C2] and extrapolated (when necessary) to 5 GHz rest frequency assuming _core - _ext = -1, are R_{min, FR I} 4 x 10^-4 (Fornax A; Morganti et al. 1993) and R_{max, BL Lac} 780 (OJ 287; Kollgaard et al. 1992). Using Eq. (C8) as before, _max (2.0 x 10⁶ 2^1-p)^1/2p ~ 9 for p = 3.

As was the case for the quasars, small values of p imply high values for the largest Lorentz factor (for p = 2, _max 30). More precisely, since _r -0.1 for the 1 Jy BL Lacs (Stickel et al. 1991), p 1.9 - 2.9 for p between 2 + and 3 + . Then _max 10 (for p = 2.9) or 38 (for p = 1.9).

The value of H₀ does affect the luminosity functions but has no direct effect on the derived beaming parameters. The fitted Lorentz factor, which is inversely proportional to the normalization of the beamed luminosity function, depends only on the ratio between the total numbers of objects (the integrals of the parent and beamed LFs). H₀ enters only because we constrain to some extent with the observed values of superluminal motion (for BL Lacs and for quasars separately; see Sec. 6.3). A higher H₀ would mean lower superluminal velocities, and in general, fits with lower ₁ are possible. We did not explore parameter space exhaustively but we show an example of a low- fit for RBL in Table 3.

It is interesting that the luminosity functions of FR I and FR II galaxies overlap smoothly, as do those of BL Lac objects and FSRQ (Figs. 14 and 17). Possibly they represent different manifestations of the same basic central engine, in which case the different radio morphologies and emission line strengths would have to be closely linked to observed radio power (Maraschi and Rovetti 1994).