


4.2 Single-Sample Goodness-of-Fit Tests
We set out in this section to consider comparison of samples, perhaps not the ideal way of conducting research, but necessary, for the following reasons. For single-sample comparison, i.e. comparison between one specific sample and a model or a sample of infinite size, we might wish to determine if there is a difference in location (e.g. mean) or dispersion (e.g. spread) in comparison to the known population. [The best-known parametric tests for sample comparison concern samples drawn from Normally-distributed parent populations; these tests are of course the ``Student''s' t-test (comparison of means) and the F-test (comparison of variances), and are discussed in most books on statistics, e.g. Martin 1971, Stuart & Ord 1994.] Is there a difference between observed and theoretical frequencies, i.e. between sample and model? Is the sample random from a known population?
Chi-square test. We have discussed this technique in some detail in
the context of model fitting via minimum  2. H0 is that the proportion
of objects in each bin is as ``expected'' (from a model or from the
presumed population). The procedure is to place the sample data into n
bins and to compute the
2. H0 is that the proportion
of objects in each bin is as ``expected'' (from a model or from the
presumed population). The procedure is to place the sample data into n
bins and to compute the  2 statistic, which is
2 statistic, which is
for (n - 1) degrees of freedom. Once this is calculated
Table A III may
be consulted to determine the significance level. If consultation of
Table A III shows that
To reiterate, the advantages of the test are its general acceptance,
its ease of computation, the ease of guessing significance and the
fact that model testing is free: vary the model parameters to turn
testing to fitting as described above. The disadvantages are the loss
of power and information via binning, and the lack of applicability to
small samples: beware of the dreaded instability at < 5 counts per
bin. Moreover, the
Kolmogorov-Smirnov one-sample test. The test is extremely simple to
carry out.
Calculate Se (x), the predicted
cumulative (integral) frequency distribution under H0.
Consider the sample of N observations, and compute
S0 (x), the
observed cumulative distribution, the sum of all observations to each x
divided by the sum of all N observations.
Find
Consult the known sampling distribution for
D under H0, as given
in Table A IV, to determine the fate of
H0. If
D exceeds a critical value at the appropriate N, then
H0 is rejected at that level of significance.
Thus as for the
The Kolmogorov-Smirnov test has some enormous advantages over the
Then why not always use it? There are perhaps two valid reasons, in
addition to the invalid one (that it is not so well known). First, the
distributions must be continuous functions of the variable to apply
the Kolmogorov-Smirnov test. The
One-sample runs test of randomness. This delightfully simple test is
contingent upon forming a binary (1-0) statistic from the sample data,
e.g. heads-tails, or the sign of the residuals about the mean, or a
best-fitting line. It is to test H0 that the sample is
random: that
successive observations are independent. Are there too many or too few runs?
Determine m, the number of heads or 1s; n, the number of
tails or 0s,
N = n + m; and r, the number of runs.
Look up the level of significance from the tabled probabilities
(Table A V) for the one or the two-tailed
test - depending on H1,
which can specify (as the research hypothesis) how the non-randomness
might occur.
The test is at its most potent in looking for independence between
adjacent sample members, e.g. in checking sequential data of say scan
or spectrum type.
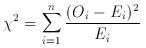
 2
exceeds a (pre-determined) critical value
for the appropriate number of degrees of freedom, H0
is rejected at that level of significance.
2
exceeds a (pre-determined) critical value
for the appropriate number of degrees of freedom, H0
is rejected at that level of significance.
 2
test cannot tell direction, i.e. It is a
``two-tailed'' test: it can only tell whether the differences between
sample and prediction exceed those that can be reasonably expected on
the basis of statistical fluctuations due to the finite sample
size. There must be something better, and indeed there is.
2
test cannot tell direction, i.e. It is a
``two-tailed'' test: it can only tell whether the differences between
sample and prediction exceed those that can be reasonably expected on
the basis of statistical fluctuations due to the finite sample
size. There must be something better, and indeed there is.
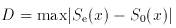
 2 test,
the sampling distribution indicates whether
or not a divergence of the observed magnitude is ``reasonable'' if the
difference between observations and prediction is due solely to
statistical fluctuations.
2 test,
the sampling distribution indicates whether
or not a divergence of the observed magnitude is ``reasonable'' if the
difference between observations and prediction is due solely to
statistical fluctuations.
 2
test. First, it treats the individual observations separately, and no
information is lost because of grouping. Secondly, it works for small
samples; for very small samples it is the only alternative. For
intermediate sample sizes it is more powerful. Finally, note that as
described here, the Kolmogorov-Smirnov test is non-directional or
two-tailed, as is the
2
test. First, it treats the individual observations separately, and no
information is lost because of grouping. Secondly, it works for small
samples; for very small samples it is the only alternative. For
intermediate sample sizes it is more powerful. Finally, note that as
described here, the Kolmogorov-Smirnov test is non-directional or
two-tailed, as is the  2
test. However, a method of finding
probabilities for the one-tailed test does exist
(Birnbaum & Tingey 1951;
Goodman 1954),
giving the Kolmogorov-Smirnov test yet another
advantage over the
2
test. However, a method of finding
probabilities for the one-tailed test does exist
(Birnbaum & Tingey 1951;
Goodman 1954),
giving the Kolmogorov-Smirnov test yet another
advantage over the  2 test.
2 test.
 2 test is applicable to data which
can be simply binned, grouped, categorized - there is no need for
measurement on a numerical scale. Secondly, in model fitting/parameter
estimation, the
2 test is applicable to data which
can be simply binned, grouped, categorized - there is no need for
measurement on a numerical scale. Secondly, in model fitting/parameter
estimation, the  2 test
is readily adapted (as we have seen) by simply
reducing the number of degrees of freedom according to the number of
parameters adopted in the model. The Kolmogorov-Smirnov test cannot be
adapted in this way, since the distribution of D is not known when
parameters of the population are estimated from the sample.
2 test
is readily adapted (as we have seen) by simply
reducing the number of degrees of freedom according to the number of
parameters adopted in the model. The Kolmogorov-Smirnov test cannot be
adapted in this way, since the distribution of D is not known when
parameters of the population are estimated from the sample.