


4.3 Tests for Comparison of Two Independent Samples
Now suppose we have two samples. We want to know whether they could have been drawn from the same population, or from different populations, and, if the latter, whether they differ in some predicted direction. Again assume we know nothing about probability distributions, so that we need non-parametric tests. There are several.
Fisher exact test. The test is for two independent small samples for which discrete binary data are available, e.g. scores from the two samples fall in two mutually exclusive bins yielding a 2 x 2 contingency table as shown in Table II.
H0 is that the assignment of ``scores'' is random.
Compute the following statistic:
This is the probability that the total of N scores could be as they
are when the two samples are in fact identical: but in fact
H0 asks,
what is the probability of occurrence of the observed outcome or one
more extreme? By the laws of probability ptot =
p1 + p2 + . . ., where
p1, p2 . . . represent values of
p for all other cases of more extreme
arrangements of the contingency table
(Siegel & Castellan 1988).
This is the best test for small samples; and if N < 20, it is
probably the only test to use.
Chi-square two-sample (or k-sample) test. Again the much-loved
H0 is that the k samples are from the same population.
Then compute
The Eij are the expectation values, computed from
Under H0 this is distributed as
Note that there is a modification for the 2 x 2 contingency table with
N objects (Table II). In this case,
The usual
There is one further distinctive feature about the
Mann-Whitney (Wilcoxon) U test. There are two samples, A
(m members)
and B (n members); H0 is that A
and B are from the same distribution
or have the same parent population, while H1 may be
one of three possibilities:
that A is stochastically larger than B;
that B is stochastically larger than A; or
that A and B differ.
The first two hypotheses are directional, resulting in one-tailed
tests; the third is not and is correspondingly a two-tailed test. To
proceed, first decide on H1 and of course the
significance level
Rank in ascending order the combined sample A +
B, preserving the A or B identity of each member.
(Depending on choice of H1) sum
the number of A-rankings to get UA
or, vice-versa, the B-rankings to get UB. Tied
observations are
assigned the average of the tied ranks. Note that if N = m
+ n,
so that only one summation is necessary to determine both - but a
decision on H1 should have been made a priori.
The sampling distribution of U is known (of
course, or there would not be a test);
Table A VI, columns labelled
cu (upper-tail
probabilities), presents the exact probability associated with the
occurrence (under H0) of values of U greater
than that observed. The
table also presents exact probabilities associated with values of U
less than those observed; entries correspond to the columns labelled
cl (lower-tail probabilities). The table is arranged
for m
where +0.5 corresponds to considering probabilities of U
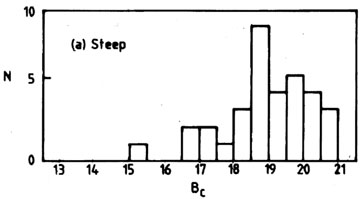
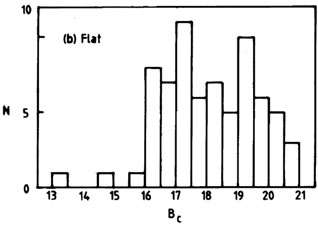
An example application of the test is shown in
Fig. 7, which
presents magnitude distributions for flat and steep (radio) spectrum
QSOs. H1 is that the flat-spectrum QSOs extend to
significantly lower
(brighter) magnitudes than do the steep-spectrum QSOs, a claim made
earlier by several observers. The eye agrees with H1,
and so does the result from the U test, in which we found
U = 719, z = 2.69, rejecting
H0 in favour of H1 at the 0.004
level of significance.
Fig. 7. An application of the
Mann-Whitney-Wilcoxon U test. The
frequency distributions are magnitude histograms for a complete sample
of QSOs from the Parkes 2.7-GHz survey
(Masson & Wall 1977),
(a) steep-spectrum objects, (b) flat-spectrum objects. H1
is that the
flat-spectrum QSOs have stochastically smaller (brighter) magnitudes
than the steep-spectrum QSOs. U = 719, z = 2.69;
H0 is rejected at the 0.004 level of significance.
In addition to the versatility, the test has a further advantage of
being applicable to small samples. In fact it is one of the most
powerful non-parametric tests; the efficiency in comparison with the
``Student's'' t test is
Kolmogorov-Smirnov two-sample test. The formulation of this test
parallels the Kolmogorov-Smirnov one-sample test; it considers the
maximum deviation between the cumulative distributions of two samples
with m and n members. H0 is (again) that
the two samples are from the
same population, and H1 can be that they differ
(two-tailed test) or
that they differ in a specific direction (one-tailed test).
To implement the test, refer to the procedure for the one-sample
test; merely exchange the cumulative distributions Se
and S0 for Sm
and Sn corresponding to the two samples.
Critical values of D are given in
Tables A VII and
A VIII.
Table A VII
gives the values for small samples, one-tailed test, while
Table A VIII
is for the two-tailed test. For large samples, two-tailed test, use
Table A IX. For large samples, one-tailed
test, compute
which has a sampling distribution approximated by chi-square with two
degrees of freedom. Then consult Table A III
to see if the observed D
results in a value of
An example is shown in Fig. 8. The frequency
distributions show the
strengths of radio emission detected at particular positions in the
sky. There was good (a priori!) reason to suspect that the positions
observed in the larger sample should result in greater detected radio
flux than the random positions of the smaller sample. The eye (a
posteriori!) suggests that this might not actually be
so. H1 is that
the distributions differ in the sense that observations of the larger
sample stochastically exceed those of the smaller: H0 = no
difference. The Kolmogorov-Smirnov test yielded D = 0.068 for
m = 290,
n = 385. Hence
The test is extremely powerful with an efficiency (compared to the t
test) of > 95 per cent for small samples, decreasing somewhat for
larger samples. The efficiency always exceeds that of the chi-square
test, and slightly exceeds that of the U test for very small
samples. For larger samples, the converse is true, and the U test is
to be preferred.
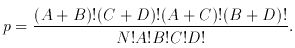
 2
test is applicable. All the previous shortcomings apply, but for data
that are not on a numerical scale, there may be no alternative. To
begin with, each sample is binned in the same r bins (a k
x r contingency table - see Table III).
2
test is applicable. All the previous shortcomings apply, but for data
that are not on a numerical scale, there may be no alternative. To
begin with, each sample is binned in the same r bins (a k
x r contingency table - see Table III).
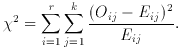
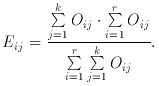
 2df = (r - 1)
(k - 1).
2df = (r - 1)
(k - 1).
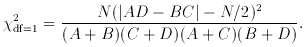
Sample . . . 1 2
Category = 1 A C
2 B D
Sample: j= 1 2 3 . . .
Category: i = 1 O11 O12
O13 . . .
2 O21 O22
O23 . . .
3 O31 O32
O33 . . .
4 O41 O42
O43 . . .
5 O51 O52
O53 . . .
. . . . . . . . . .
. . .
 2 caveat
applies - beware of the dreaded number 5, below
which the cell populations should not fall. If they do, combine adjacent
cells, or abandon the test. And if there are only 2 x 2 cells, the total
(N) must exceed 30; if not, use the Fisher exact probability test.
2 caveat
applies - beware of the dreaded number 5, below
which the cell populations should not fall. If they do, combine adjacent
cells, or abandon the test. And if there are only 2 x 2 cells, the total
(N) must exceed 30; if not, use the Fisher exact probability test.
 2 test (and the
2 x 2 contingency table test); it may be used to test a directional
alternative to H0, i.e. H1 can be
that the two groups differ in some
predicted sense. If the alternative to H0 is
directional, then use
Table A III in the normal way and halve the
probabilities at the heads
of the columns, since the test is now one-tailed. For degrees of
freedom > 1, the
2 test (and the
2 x 2 contingency table test); it may be used to test a directional
alternative to H0, i.e. H1 can be
that the two groups differ in some
predicted sense. If the alternative to H0 is
directional, then use
Table A III in the normal way and halve the
probabilities at the heads
of the columns, since the test is now one-tailed. For degrees of
freedom > 1, the  2 test
is insensitive to order, and another test may
thus be preferable. One that almost always is preferable is the following.
2 test
is insensitive to order, and another test may
thus be preferable. One that almost always is preferable is the following.
 . Then
. Then
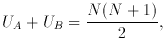
 n, which
presents no restriction in that group labels may be interchanged. What
does present a restriction is that the table gives values only for
m
n, which
presents no restriction in that group labels may be interchanged. What
does present a restriction is that the table gives values only for
m  4 and n
4 and n  10. For samples up
to m = 10 and n = 12, see
Siegel & Castellan (1988).
For still larger samples, the sampling distribution
for UA tends to Normal distribution with mean
µA = m (N + 1)/2 and
variance
10. For samples up
to m = 10 and n = 12, see
Siegel & Castellan (1988).
For still larger samples, the sampling distribution
for UA tends to Normal distribution with mean
µA = m (N + 1)/2 and
variance  A2 = mn (N +
1)/12. Significance can be assessed from the
Normal distribution,
table I
of Paper I, by calculating
A2 = mn (N +
1)/12. Significance can be assessed from the
Normal distribution,
table I
of Paper I, by calculating
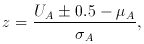
 that
observed (lower tail), and -0.5 for U
that
observed (lower tail), and -0.5 for U  that observed
(upper-tail). If the two-tailed (``the samples are distinguishable'')
test is required, simply double the probabilities as determined from
either Table A VI (small samples) or the
Normal distribution approximation (large samples).
that observed
(upper-tail). If the two-tailed (``the samples are distinguishable'')
test is required, simply double the probabilities as determined from
either Table A VI (small samples) or the
Normal distribution approximation (large samples).
 95
per cent for even moderate-sized
samples. It is therefore an obvious alternative to the chi-square
test, particularly for small samples where the chi-square test is
illegal, and when directional testing is desired. An alternative is
the following:
95
per cent for even moderate-sized
samples. It is therefore an obvious alternative to the chi-square
test, particularly for small samples where the chi-square test is
illegal, and when directional testing is desired. An alternative is
the following:
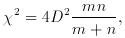
 2
large enough to reject H0 in favour of
H1 at the desired level of significance.
2
large enough to reject H0 in favour of
H1 at the desired level of significance.
 2
= 3.06 for 2 degrees of freedom; the associated
probability is 0.25, a very boring number, and quite inadequate to
allow rejection of H0 in favour of H1.
2
= 3.06 for 2 degrees of freedom; the associated
probability is 0.25, a very boring number, and quite inadequate to
allow rejection of H0 in favour of H1.