


3. The Cosmological redshift
One observable prediction of an expanding universe is that of redshifting. When a light wave is traveling from a distant galaxy, to our own, it must travel through the intervening spacetime. This results in a stretching of the wavelength of light, since the spacetime is expanding. This longer wavelength results in the light being shifted to a `redder' part of the spectrum. Of course light with wavelengths differing from visible light will not be visible to the human eye, but they will still be shifted to longer wavelengths.
To quantify this analysis, consider a light ray which must travel
along a null geodesic (ds2 = 0) in the comoving frame with
constant  and
and
 . Using (4),
. Using (4),
so,
Integrating yields,
where te is the time the light pulse was emitted,
t0 was the time the light pulse was received, and
re is
the distance to the galaxy. Thus, if one knows a(t) and k, one
can find the relation between the distance and the time. However,
consider emitting successive wave crests in such a brief time that
a(t) is not given a chance to increase by a significant amount;
i.e., the waves are sent out at times te and
te +
Subtracting (6) from this equation and using the
fact a(t) doesn't change, one can use the fundamental theorem of
calculus to obtain,
or
c
Here a(t0) is the scale factor of the universe
as measured by
a comoving observer when the light is received,
a(te) is the
scale factor when the light was emitted in the comoving frame,
In addition to this cosmological redshift, which is due to the
expanding universe, there can also be gravitational redshifts and
Doppler redshifts. At great distances the former two can be
neglected, but in local cases all three must be considered.
It must also be stressed that the Special Relativity (SR) formula
for redshift can not be used. This is because SR only holds for
`local' physics. Attempting to use this across large distances
can result in a contradiction. For example, the expansion rate of
the universe can actually exceed the speed of light at great
distances. This is not a violation of SR, because a `chain' of
comoving particles (galaxies) can be put together, spaced so the
laws of SR are not violated. By summing together the measurements
of each set of galaxies, one finds the expansion rate to exceed
that of light, although locally SR holds locally
[9]. Another
explanation is that in a universe
described by SR, no matter or energy exists and the metric never
changes. On the contrary, in an expanding spacetime none of these
requirements are true. Although, SR continues to hold locally,
since a `small enough' region can always be chosen where the
metric is approximately flat.
(12)
12 One must be careful by what
is meant by `small enough'. This technical point need not concern
us with the present discussion, see
[12].
Back.
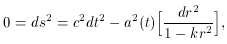
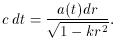

 te and received at times t0 and
t0 +
te and received at times t0 and
t0 +
 t0,
respectively. Then (6) becomes,
t0,
respectively. Then (6) becomes,

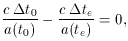
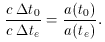
 t is just the
wavelength,
t is just the
wavelength,  . Thus, it
follows that the red shift, z, can be defined by
. Thus, it
follows that the red shift, z, can be defined by
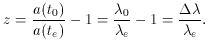
 0 is the
wavelength observed and
0 is the
wavelength observed and
 e is the
wavelength when emitted. It is clear that z will be positive,
since a(t0) > a(te),
that is the universe is getting larger.
e is the
wavelength when emitted. It is clear that z will be positive,
since a(t0) > a(te),
that is the universe is getting larger.