


 )
)The Higgs potential and the corresponding inflationary scenario were based on two ideas: (1) the Higgs potential is needed in other branches of particle physics (one does not have to shoulder the burden of inventing it) and (2) the preinflationary stage was assumed to be an extremely hot universe; this is a simple extrapolation of our current knowledge about the 3 K background, nucleosynthesis, etc.
However, both of these premises have been losing some of their appeal in recent years:
(1) There is a direct argument for the existence of scalar fields. In the supersymmetry theories, the existence of scalar fields is a consequence of existence of the experimentally verified spin- 1/2 fields - the electron quarks, etc.
Those scalar fields which have not yet been experimentally observed
may have a V( ) without a
maximum. The form V =
(
) without a
maximum. The form V =
( /4)
/4)
 4 is appealing,
because
4 is appealing,
because  is
dimensionless. The simple form
1/2 µ2
is
dimensionless. The simple form
1/2 µ2
 2 is also not
excluded, although the question of what can be used to calculate µ
arises in this case.
2 is also not
excluded, although the question of what can be used to calculate µ
arises in this case.
(2) "Complete" cosmological theories (see, for example, (Quantum Gravity 1984)) which intend to describe the spontaneous birth of the universe are now more fashionable than before. This is a case of feedback from the inflationary expansion theory - we shall explain this loose statement in the last section of the paper.
In the spontaneous creation scenario, one can imagine the birth of a very small closed universe with a large, already-imprinted scalar field. This field is coherent (or almost coherent) and uniform precisely because the newborn universe is very small.
The new approach proposed by
Linde (1983)
is to look at (8.1), (8.2),
and (8.3) in Section 8 with a monotonic
V( ) and the following initial
conditions: large
) and the following initial
conditions: large  , small a,
and an already-built-in expansion velocity
H > 0. I will illustrate this approach for the case V =
1/2 µ2
, small a,
and an already-built-in expansion velocity
H > 0. I will illustrate this approach for the case V =
1/2 µ2
 2, omitting
the curvature term in (8.3). We assume that
2, omitting
the curvature term in (8.3). We assume that
 2 is much less
than µ2
2 is much less
than µ2
 2
and can be neglected (we shall see later on what the domain of applicability
of this assumption is) and use units in which
2
and can be neglected (we shall see later on what the domain of applicability
of this assumption is) and use units in which
 = c = 1. We
then introduce the Planck mass M = MPl =
G-1/2 in place of G. In the
CGS system, G = 6.67 x 10-8
cm3f-1s-2 and
= c = 1. We
then introduce the Planck mass M = MPl =
G-1/2 in place of G. In the
CGS system, G = 6.67 x 10-8
cm3f-1s-2 and
The second equation, (8.2), can be written in the form
In the first equation, (8.1), we neglect
where the initial conditions are t = 0,
The radius of the universe is now given by
where the upper limit of the integral is the time t1
at which
It is well known that cosmology requires an inflationary expansion of
at least a factor of 1030 = e70. Therefore,
we require
We shall now repeat the sequence of the calculations in simple words.
We take the case of a scalar field that has no exact solution:
If the mass of the scalar particles µ is much smaller than
the Planck
mass, M = 10-5 g (= 1019 GeV), then the
initial
The ideal de Sitter solution, exp (H0t), is now changed to
exp (
The regime changes simultaneously at all points in space. When
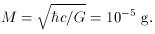
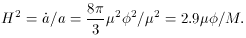
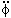 compared to
3H
compared to
3H :
:
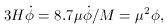
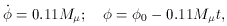
 =
=
 0 and
a = a0.
0 and
a = a0.
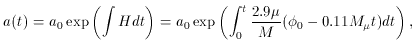
 has fallen
to zero; the approximations we made above fail somewhat earlier, but
this does not change the final result. We obtain
has fallen
to zero; the approximations we made above fail somewhat earlier, but
this does not change the final result. We obtain
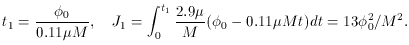
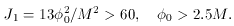
 = const
and V(
= const
and V( ) = 0, i.e., there is
no "false vacuum". It turns out that one can
still construct an expanding cosmological solution. The scalar field
decreases more slowly than in the flat Minkowski case: the expansion
plays the role of a brake or friction. Given a high enough initial
) = 0, i.e., there is
no "false vacuum". It turns out that one can
still construct an expanding cosmological solution. The scalar field
decreases more slowly than in the flat Minkowski case: the expansion
plays the role of a brake or friction. Given a high enough initial
 0, the
expansion that occurs during the slow decrease in
0, the
expansion that occurs during the slow decrease in
 is large enough.
is large enough.
 0 is much greater
than µ, but only on the order of 2.5-4 times larger than the Planck
mass M.
0 is much greater
than µ, but only on the order of 2.5-4 times larger than the Planck
mass M.
 H
dt). The beautiful symmetry of the de Sitter solution is lost.
However, this is an achievement of the theory; not a deficiency. This
makes the transformation from the inflationary de Sitter
H0t or
quasi-de Sitter
H
dt). The beautiful symmetry of the de Sitter solution is lost.
However, this is an achievement of the theory; not a deficiency. This
makes the transformation from the inflationary de Sitter
H0t or
quasi-de Sitter  H(t) dt
solution to the plasma solution easier.
H(t) dt
solution to the plasma solution easier.
 becomes of order µ, the universe goes into an oscillatory regime in
which
becomes of order µ, the universe goes into an oscillatory regime in
which 
 cos µ t; the
scalar particles then decay into plasma.
However, this is beyond the scope of our review. One difficult (and as yet
unsolved) question is, to what extent was the spatial uniformity of
cos µ t; the
scalar particles then decay into plasma.
However, this is beyond the scope of our review. One difficult (and as yet
unsolved) question is, to what extent was the spatial uniformity of
 0
created during the birth of the universe and to what extent is it required
as an initial condition? What would happen if
0
created during the birth of the universe and to what extent is it required
as an initial condition? What would happen if
 0 were nonuniform?
Linde argues that the region with the largest initial
0 were nonuniform?
Linde argues that the region with the largest initial
 0 expands more
rapidly; its final volume will be much larger than that of the regions that
start out with smaller
0 expands more
rapidly; its final volume will be much larger than that of the regions that
start out with smaller  0,
so that those regions will be unimportant. His
idea is that one can begin with random values of
0,
so that those regions will be unimportant. His
idea is that one can begin with random values of
 0 in
different regions
of space; the inflationary process will choose the region with maximum
0 in
different regions
of space; the inflationary process will choose the region with maximum
 0 by itself and smooth
out the effects of nonuniformity. This is why this
is called the "chaotic theory". We shall not discuss this theory any
further, but discuss some simpler points instead.
0 by itself and smooth
out the effects of nonuniformity. This is why this
is called the "chaotic theory". We shall not discuss this theory any
further, but discuss some simpler points instead.