4.2.2. The Solar Neighborhood

The structure of the Galaxy can be divided into three distinct kinematical regions that are defined by particular ratios of rotational velocity (V_c) to velocity dispersion (_v). These regions are known as the thin disk, the thick disk and the halo. Their vertical density distribution, (z) assumes the form

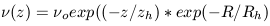
(7)

where z_h is the vertical disk scale height and R_h is the radial disk scale length. This exponential form can be derived by assuming an infinitely thin disk (which is justified by the observations) together with an isothermal velocity distribution. In the case of a self-gravitating disk (z) goes as sech². The self gravity in this case is provided by the sum of the stellar distribution and the dark matter distribution. The Solar Neighborhood is a region of of radius roughly 300 light years that contains a few thousand stars. This region contains thin disk, thick disk and halo stars and their normalization is important to the determination of the mass density within this region.

The Thin Disk: This is a coherent and highly rotating component. The average value of _v / V_c is 0.1 and the scale height is 100 pc. Since the total disk diameter is 30 kpc the thin disk has a thinness ratio of .003. Most of the molecular gas, and hence massive star formation in the Milky Way, is concentrated in the thin disk.

The Thick Disk: The existence of this component is still somewhat uncertain, although it seems to be required to account for the observed star counts in the solar neighborhood as well as the observed stellar metallicity as a function of height above the galactic plane. Zinn and West (1984) also identified a population of Globular clusters that has disk like kinematics. Estimates of z_h range from .7 -1.1 kpc with some as high as 1.5 kpc. These estimates vary according to the particular sample of stars which is used. A fair tracer of the thick disk population has not been unambiguously identified (see von Hippel and Bothun 1993). The value of _v, however, is well determined at 45 ± 5 km s^-1, making _v / V_c 0.25. Unfortunately, the thick disk is sometimes confused with the old thin disk, which has z_h 300 pc. The higher value of z_h for the old thin disk stars is a consequence of their many orbits about the center of the galaxy and the cumulative effects of small gravitational scattering off of other stars (see Chapter 3). This acts like a diffusion process which causes the stars originally born in the very thin disk to diffuse vertically.

The Bulge/Halo: These are the spheroidal components of galaxies that are supported by internal velocity dispersion instead of large scale rotation. The orbits of the stars can be anisotropic and so the spheroidal component is not necessarily always round. The bulge portion of the spheroid is a regime of high stellar density over a fairly small scale. The halo is best defined by the GCS of the galaxy. It is a large, very low density collection of old stars. These stars were the first to form in the galaxy as it was collapsing (Chapter 5). There is very little rotation in the galactic halo so _v / V_c substantially exceeds 1. The overall scale size of the halo component is difficult to ascertain as there are few stars which trace it. For spheroidal systems, the fall off in surface density is

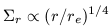
(8)

where r_e is the effective radius defined to enclosed 50% of the light. For the high density bulge, r_e is likely to be less than 2 kpc (Gilmore et al. 1989; Sackett 1997). For the halo, r_e lies in the range of 3-7 kpc (Bothun et al. 1991).

The solar neighborhood lies about 8.5 kpc from the center of the Galaxy (see Sackett 1997). At that distance, there are very few, if any, true bulge stars. Hence, the solar neighborhood stars are a mixture of thin disk, thick disk and halo stars. Each of these three components have different kinematical and metallicity distributions and it is possible to assign nearby stars to these three components on the basis of observations. Halo stars in the solar neighborhood are extremely rare (hence the difficulty in finding the population II main sequence from a trigonometric parallax sample) with roughly 1 out of every 500-800 stars belonging to this population. The normalization of the thick disk, however, is quite uncertain with values of 2-15% consistent with various samples. There is covariance between the determination of the normalization and z_h with larger values of z_h resulting in lower normalizations. This covariance is a consequence of the fitting procedure keeping the total numbers of stars in the thick disk to be relatively constant.

In a highly flattened rotating stellar system, the density distribution in the vertical (z) direction, is a measure of the surface mass density. This situation arises as Poisson's equation for a flattened system assumes the form

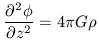
(9)

As the density increases, then the z-coordinate sees a larger derivative in the potential which means it experiences a larger gravitational restoring force in that direction. In practice, this gravitational restoring force can be estimated by measuring z_h and the vertical velocity dispersion _v for some well defined sample of stars. This transformation from equation 9 to observables makes use of a variant of the collisionless Boltzmann equations. Since stars are not escaping from this system, the collisionless Boltzmann equation can be combined with the equation for continuity of mass to yield (see Binney and Tremaine 1987 for details):

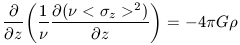
(10)

Measurements of the density distribution of stars in the z direction, (z), combined with the vertical velocity dispersion then constrains .

The first attempt to utilize equation 10 to constrain the solar neighborhood mass density was by Jan Oort in 1932 who derived a mass density of 0.15 M pc^-3. Of course, Oort had no knowledge of the presence of another kinematic system, the thick disk, and so he explicitly assumed that his sample of F stars and K giants was tracing out a few thin disk scale heights. Under that assumption, Oort found that the equivalent surface density of the thin disk in an imaginary cylinder of height 700 pc was 90 M pc^-2.

A more recent determination of these parameters has been done in a series of papers in the early 80's by John Bahcall and collaborators. Again using samples of A and F stars, they derive estimates for ₀ of 0.18 - 0.21 M pc^-3 and an equivalent surface mass density out to 700 pc of 75 M pc^-2. The measured luminosity function of stars in this imaginary cylinder gives an equivalent surface luminosity density of 15 ± 2 L pc^-2. This is equivalent to a mean blue surface brightness of 23.0 mag arcsec^-2. Bahcall's sample gives a mean M / L in the solar neighborhood of 5.

Testing for the presence of dark matter in the solar neighborhood now becomes an accounting problem The possible sources of this mass in the solar neighborhood are 1) luminous stars, 2) interstellar gas, 3) stellar remnants (mostly white dwarfs) and 4) dark matter:

Luminous stars: Determinations of the local luminosity function of stars can yield a mass function if the bulk of the stars are main-sequence stars where the relation between luminosity and mass is well-determined. This is the case in the solar neighborhood. The observed value of = 0.044 M pc^-3 is well short of the required value (e.g., Gilmore et al. 1989).

Gas: Since stars form from gas with an overall efficiency of 1-20% (depending upon many factors), then every star formation event should leave behind plenty of gas. The local volume mass density of gas has been measured at = 0.042 M pc^-3; not surprisingly, almost identical to the stellar value. The consideration of stars + gas accounts for one-half the inferred volume mass density.

Stellar Remnants: Since stellar remnants are no longer producing energy they necessarily have high values of M / L and are hard to detect. This makes an accurate determination of their local space density quite difficult. Models of star formation in the solar neighborhood, combined with estimates of the initial mass function and mass loss rates in post main sequence evolution can be used to predict the remnant density. The detectability of white dwarfs is also dependent upon their cooling rate and hence the inferred remnant density is strongly dependent upon the assumed age of the galactic disk in the solar neighborhood. None of these parameters is very well determined. Currently values of = 0.01 - 0.03 M pc^-3 are consistent with the observations, though most determinations cluster around the upper end. A reasonable upper limit to the density of stellar remnants is = 0.044 M pc^-3, since the galaxy is not yet old enough to have a mean remnant mass density higher than the observed mass density of low mass stars.

Adding the observed densities of stars,gas and stellar remnants gives ₀ in the range 0.096 - 0.13 M pc^-3. This implies at least 0.05 M pc^-3 of dark matter, or roughly 1/3 of the total dynamically inferred volume mass density. This is taken as evidence for significant amounts of dark matter in the solar neighborhood. However, we have ignored the thick disk contribution to the observed column of 75 M pc^-2.

In a long series of papers, Gerry Gilmore and collaborators have taken this assumption to task and have persuasively argued that omission of the thick disk has serious consequences on the question of dark matter in the solar neighborhood. In their most recent analysis, Kuijken and Gilmore (1991) derive a surface mass density of 71 ± 6 M pc^-2 (i.e., the same as the Bahcall value) but conclude that only 48 ± 9 M pc^-2 is associated with thin disk material near the sun. The remaining 1/3 is associated with the thick disk and halo which has not been accounted for in our previous census. It is difficult to find fault with this analysis and hence the establishment of the thick disk has essentially resolved the Oort limit problem thus removing any credible evidence for the presence of dark matter in the solar neighborhood.