4.2.3. Galactic Scales

Mass distributions and predicted rotation curves

Figure 4-2 shows an image of a typical edge-on spiral galaxy where the thin disk and central bulge concentration are evident. If the distribution of light traces the distribution of mass, then we would expect a high mass concentration that corresponds with the bulge light. In that case, the galaxy is similar to the point mass approximation that governs solar system orbits. From the Virial Theorem, V_c² M / R and hence orbital velocity should decline as R^-1/2.

Figure 4-2: CCD image of the nearly edge-on spiral NGC 253 taken by the Author. Note the relatively thin disk and bright central light concentration.

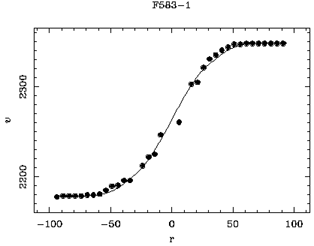
Rotation curves of galaxies were first systematically studied by Vera Rubin and her colleagues starting in the late 60's. Those initial observations showed that no spiral galaxies exhibited a rotation curve which scaled as R^-1/2. Instead, rotation curves were mostly flat with R. A typical rotation curve for a spiral galaxy is shown in Figure 4-3. These data show that the point mass approximation is invalid and another form for the potential is necessary.

Figure 4-3: Typical optical rotation curve for a disk galaxy that shows a sharp rise and then a relatively flat region out to the optical radius. Data courtesy of E. de Blok.

The luminosity profiles of disk galaxies exhibit an exponential fall off. Does this provide a clue to the form of the potential? If the mass distribution is also exponential then we have

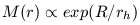
(11)

For this exponential mass distribution there is some value of R which maximizes this expression

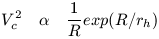
(11a)

This equation can be solved numerically to show that the maximum rotational velocity occurs at R_max 2.2r_h. Strictly speaking, this result is only valid for the case of a spherical distribution of mass. The case of a flattened distribution, however, yields a similar value for R_max and a peak rotational velocity which is 15% higher than the case of the exponential sphere (see Figure 2-17 in Binney and Tremaine).

For the general case of a rotating system where the virial theorem applies, the mass enclosed in some radius, r is given by equation 6f. For the point mass approximation, v_c goes as R^-1/2 and there is no dependence of M(r) on r. Flat rotation curves indicate that v_c is not a function of r and hence M(r) increases with scale. Since galaxies are obviously finite in mass, there must be a limit to this increase. Moreover, the light profile of galaxies decreases in intensity as r increases. Hence flat rotation curves demand the presence of an extended mass distribution which is not reflected in the light distribution. This extended mass distribution is generally assumed to be in the form of a spherical halo. In the derivation of the dynamical friction timescale (see Chapter 3) we made use of a specific halo density distribution. This density distribution again is

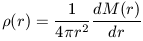
(12)

Since M(r) = v_c² r / G then dM(r) / dr = v_c² / G so that

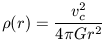
(12a)

For this halo we also specify M(r) goes as < >R³. Substituting this into equation 12a recovers equation 6f.

The kind of potential that can give rise to the density distribution given in equation 12 is often called an isothermal sphere. In order to achieve a balance between outward pressure and inward gravity, an isothermal sphere must satisfy the equation of hydrostatic equilibrium

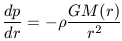
(13)

For an ideal gas composed of one particle of mass m, p = nkT and = nm. Therefore

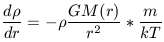
(14)

where T is the constant Temperature. The usual way to solve this differential equation is to multiply both sides by r² / and differentiate each side with respect to r. Since this is a sphere then M(r) = 4/3 r³ and dM(r) / dr = 4 r² we have

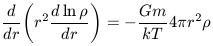
(15)

For this differential equation we can try a solution of the form = Cr^-n. For the left hand side we have:

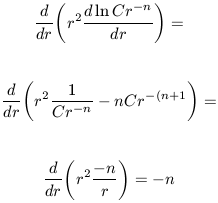
(16)

The right hand side is

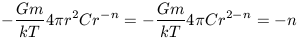
(16a)

which is solved as

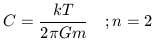
(16b)

Hence r^-2 gives rise to a potential in which v_c is not dependent on r. In general, the power law exponent in the density distribution does not have to be -2 to produce a flat rotation curve and the generalized halo density profile is

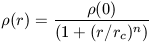
(17)

where (0) is the central mass density and r_c is the core radius of the halo. A well-defined rotation curve, in which the luminous contribution to the mass distribution has been accounted for, can constrain (0),r_c and n.

Observational Evidence for Flat Rotation Curves

The unambiguous identification of rotation curves in which v_c does not decline as a function of r provides very powerful evidence for the presence of a mass distribution that is like an isothermal sphere. For the case of an exponential mass distribution, the surface brightness at R_max is down by approximately 2.5 mag arcsec^-2 relative to µ(0). For a typical disk galaxy this corresponds to a mean blue surface brightness level of 24.0 mag arcsec^-2, which is 1.5 mag fainter than the sky. This makes detection of stellar absorption lines and the subsequent determination of stellar rotational velocities at that radius very difficult. Without data beyond R 2.5 r_h, flat rotation curves by themselves do not provide good evidence for an extended halo mass distribution that dominates the disk dynamics. The data is still consistent with a simple exponential mass distribution. To make further progress requires the construction of rotation curves that reached well beyond 2.5 r_h using one of the following techniques:

Using optical emission lines as the velocity tracer: These lines usually arise from the ionization of hydrogen by hot stars. If there is sufficient star formation in some spiral galaxy at r 2.5 r_h, then that galaxy's rotation curve will provide a good check on the existence of an extended mass distribution. In general, there are few spirals that have such an extended region of star formation. Observations of about 100 such objects by Schommer et al. (1993) have revealed a mixed collection of rotation curves. Some are flat, some are still rising at the last measured point and some are falling which indicates and end to the mass distribution. Figure 4-4 shows some examples of these kinds of rotation curves. This data is consistent with an extended halo mass distribution but not conclusive.

Figure 4-4: Collection of rotation curves from a variety of galaxies of varying circular velocity. While all generally show a steep rise and flat region, there is significant variation about this basic structure.