4.3.5. Clusters of Galaxies
Clusters of galaxies are a few dynamical timescales old and
we can apply the virial theorem to them. From this,
a simple scaling argument suggests that clusters of
galaxies must have more dark matter in them than individual galaxies.
Virial masses scale as vc2R. For clusters
of galaxies vc2
is replaced by the velocity dispersion
v and R refers to
cluster radius, a somewhat ill defined quantity. For galaxies,
vc is
250 km s-1 on a
scale R
10 kpc. For
clusters v is
1500 km s-1 on a
scale of R
1 Mpc.
To reproduce this much cluster mass from
the sum of individual galaxies each with vc = 250 km
s-1 would therefore
require a total population of 3600 within R = 1 Mpc. Real clusters,
however, only have few 100 galaxies with masses appropriate to
vc = 250 km s-1
and hence there is a notable excess of matter in clusters compared that
in the individual galaxies. Accounting for the observed hot X-ray gas
in clusters only gains an extra factor of 2 in observed mass.
So far we have just blindly applied the virial theorem (2T + W = 0) to
gravitational potentials to derive masses. In this application we have
not been very picky over what value of scale factor, R, to use.
There are, however, two different physical situations which can arise:
1) A system of massless tracer particles moves through a large potential
or 2) a self-gravitating system of N-particles where the mass of the
system is contained in those N particles. For the first case, the
radius of the potential as defined by the tracer particles is
appropriate to determine R. In the second case, the mean separation
between the particles is a better choice to determine R. A
compromise between these two extremes is to choose a quantity called
the median radius, rm, which is the radius that
encloses half of
the system's mass. In most simple stellar systems, rm
R so that
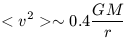
| (19) |
which is only slight different than the coefficient of 0.5 found in equation 6f.
In astrophysical units, equation 6f can be expressed as
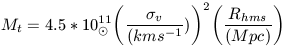
| (20) |
Application of equation 20 to real clusters of galaxies has three potential sources of systematic error which can affect the derived mass.
1. Although the virial theorem is valid after only one dynamical timescale,
the observational estimator
(v) of the true
r.m.s velocity is more reliable if the
system is several dynamical timescales old. Since the epoch of initial
cluster collapse is not well known (see Chapter 5),
clusters of galaxies may only be 1-3 dynamical timescales old.
The noise in the v
estimator
depends upon 
N and so this
is mostly a problem for groups or small clusters.
2. Usually < Rhms > is calculated from the
galaxy (e.g., the light) distribution in the cluster. If there is no
bias between the distribution of light and mass on the scale of the
cluster, then this will provide a proper estimation of the length
scale to be used. However, N-body simulations of cluster formation
which are dominated by dark matter often show that the luminous
galaxies (the baryonic material) is more centrally condensed
than the dark matter distribution. Presumably, this is because
the baryonic material is more dissipative than the particular brand
of dark matter that was chosen. If this is the case, then using
< Rhms > from galaxy positional data clearly biases the
estimation of Mt to low values.
Moreover, this is a situation where the bulk of the mass lies in some
smooth distribution and not in N discrete particles and masses should
be calculated from
v2
R, where R is the half mass radius of the cluster.
West and Richstone (1988) used this idea to suggest that cluster virial
masses, and the subsequent derivation of M / L are too low by as much
as a factor of 10. A more recent analysis by Evrard et al. (1996)
shows the situation is not nearly this extreme.
3. Application of the virial theorem implicitly assumes that only one
potential is being probed by
v. Clearly, if
clusters have substructure
in them which has not been assimilated into the main potential, then
there are multiple potentials and the observed value of
v
has no physical meaning in the context of the virial theorem. At
least one excellent case study exists to illustrate this point.
Substructure and the Illusion of Large M / L
The Cancer cluster is a spiral-rich cluster located at a distance
of about 3 times the distance to Virgo. Based on a few redshifts
used to determine v,
Tift et al. (1973) derived
derived an overall M / L of
1700. This is an enormously high value and, if representative,
suggests that clusters of galaxies have at least an order of magnitude more
unseen matter in them than do individual galaxies.
Bothun et al. (1983) obtained a considerably different interpretation
of the Cancer cluster. Using a nearly complete redshift survey,
they showed there was a correlation between position within the
cluster and redshift. This is reproduced in
Figure 4-5. This correlation
allowed specific dynamical units to be discovered in what was
previously considered to be a single dynamical unit.
The analysis of Bothun et al. showed that the Cancer cluster in reality
was a collection of five distinct subgroups that when projected
onto the plane of the sky appeared to be a single cluster.
Moreover, these groups
are not even gravitationally bound to one another but instead are
separating with the Hubble flow. Bothun et al. were able to lower
M / L from 1700 down to 100-200, the value found for each of the
individual groups.
|
Figure 4-5: Postion-velocity correlation for galaxies in the Cancer cluster. Each letter designates a different group separated in redshift space from another group. The clustering of letters together indicates that the Cancer cluster is not a real cluster but instead is a collection of individual small groups. From Bothun et al. (1983). |
Although Cancer is somewhat of an extreme case, the issue of the frequency of substructure in clusters remains unresolved. While its likely that every cluster has some substructure if examined with sufficient resolution, the issue is how much of the cluster mass is tied up in these substructures. Substructure is very difficult to unambiguously detect. At its lowest level, substructure would manifest itself via the appearance of secondary maxima in galaxy positional data. However, galaxy positional data is usually only available for 50 - 200 galaxies and the resultant Poisson noise fluctuations can generate statistically insignificant secondary peaks. The combination of velocity and positional data greatly improve upon this. Position-velocity correlations, to first order, can isolate dynamical subgroups within an overall structure. However, while this is a necessary condition, it is not a sufficient one to unambiguously identify substructure.
For instance, it is now clear
that most virialized clusters are surrounded by a lower density
region of galaxies that are presently infalling.
If their infall trajectory is projected
along the line of sight to the cluster core, a position velocity
diagram will not necessarily indicate that these galaxies aren't
in the core. Clearly, the inclusion of an infalling population
raises v. To resolve
this ambiguity requires very accurate
measures of relative distances so that the infalling group can be
isolated in physical space, even though it blends with the cluster
core in redshift space. In general, such distances are not available
and so infall remains a worrisome complication in interpreting
the measured v for
clusters. Indeed, as
more clusters are studied in detail, the frequency of
occurrence of substructure has increased from about 25-30% of
all clusters in 1982 to 50-75% by now (see West and Bothun
1990; West et al. 1995). Since the clusters themselves
haven't done much dynamical evolution on the decade timescale, this
increase can only be attributed to closer inspection by observers. The major
physical attribute which is missing from most all determinations of
substructure, however, is the amount of mass involved in it relative to
the main cluster.
X-ray studies of clusters of galaxies have the potential to provide more physical discrimination than position-velocity data. Potential well depth determines the virial temperature of the X-ray emitting plasma. An infalling group of lower mass than the total cluster mass will have a cooler temperature. Therefore, perhaps the best physical indicator of substructure in clusters at the level where it is dynamically important is the existence of multiple temperature components in an X-ray image of a cluster. As mentioned previously, the Einstein satellite could not make this measurements but ROSAT could and did. Indeed, the ROSAT observations of the Coma cluster, the quintessential example of a dense, post-virialized cluster, does show examples of multiple temperature components in its cluster core and hence substructure (see Briel et al. 1992). Similar substructure is also seen in the ROSAT data for A2151 (Huang and Sarazin 1996).
Another physical indicator of substructure is provided by gravitational lensing. Figure 2-24 shows a spectacular HST picture of the galaxy cluster A2218. Numerous arclets and rings can be seen. These are the distorted (lensed) images of resolved galaxies located behind the cluster. The orientation and degree of curvature of these features depends upon the cluster mass distribution and the amount of substructure. Analysis of the A2218 observations are most interesting because this would represent the first case where substructure in the dark matter distribution might be directly inferred instead of inferring it indirectly on the basis of substructure in the light (baryonic) distribution. The analysis by Squires et al. (1995) show that inferred peak of the 2D dark matter distribution is coincident with the optical and X-ray centers. They also derive a total M / L for A2218 of 440 ± 80.
Recent work on gravitational lenses also underscores how critical the
very central mass distribution is, in a cluster of galaxies, in determining
the overall arclet morphology and extent. For instance,
the presence of a central dominant cluster
galaxy (a cD galaxy) can inhibit the formation of radial arcs
(see Miralda-Escude and Babul 1995). Detection
of radial arcs (e.g., Newbury and Falhman 1996) then limits the amount of
mass that can be present in the very core of the cluster. Flores and
Primack (1996) give a general treatment of lensing in which they show
that the nature of the lensing is a very sensitive function of the
core properties of the lensing mass itself.
Fischer
and Tyson (1997), show that one luminous X-ray cluster located at z=0.45
shows lensing behavior that comes from two components: 1) a strong
central mass concentration and 2) substructure located
1.5 Mpc
from the cluster core. This strongly suggests the process of infall and
cluster merging is happening at this redshift.
In sum, because of substructure and infall, M / L determinations of clusters of galaxies made on the basis of cluster dynamics are rather unreliable. Reported values in excess of 1000 are almost certainly wrong as substructure has not been taken adequately into account. When it is, clusters seem to define an M / L regime of 200-500, still larger than individual galaxies but not extremely so. If the Universe is closed, clusters of galaxies contribute 10-20% of the closure density and hence the dark matter must be distributed on still large scales and occupy the space between clusters.