4.4. The Large Scale Distribution of Dark Matter

Observational determinations of the large scale distribution of dark matter make use of the peculiar velocity formulation discussed in Chapter 3. For the local case of Virgocentric flow, the infall velocity and the position of the Local group is driven by two competing sources of acceleration. On the one hand, the gravitational acceleration is driven by the amount of mass overdensity / in the Virgo cluster. On the other hand, this mass overdensity must compete against the average mass density of the Universe (e.g., ).

As a case in point, let's now consider the infall of the Local Group towards Virgo. We assume a cosmic velocity of 1500 km s^-1 for Virgo and a LG infall velocity of 250 km s^-1. The observed value in light of / is 2 (Bushouse et al. 1985; Tully and Shaya 1984; Tonry and Davis 1981). For = 1, application of equation 3.39 yields

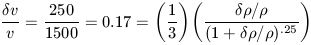
(21a)

which is solved with / 0.6. This is significantly less than the observed value and readily implies that the distribution of light is more strongly clustered than the distribution of mass on this scale of 1500 km s^-1. In an = 0.1 Universe we have

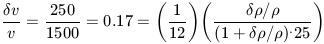
(21b)

which is solved with / 3.0. This density contrast is closer to the observed value in light ( / 2.0) and requires little or no biasing.

This simple model shows the degeneracy between the biasing factor and the value of inferred from peculiar velocity data. While ideally the peculiar velocity field is a direct reflection of the large scale density field, the presence of possible bias between the mass and light distributions is a complicating factor. In practice it is only the first order component

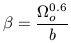
which can be recovered from the data. Clearly, the best thing to do is to select a sample in which b 1. This is difficult to do a priori but there has been significant effort along these lines.

The most robust attempt is the POTENT effort (see Bertschinger et al. 1990; Dekel et al. 1993) in which the large scale density field as defined in redshift surveys is used to predict the peculiar velocity field. This is a purely local approach where peculiar velocities in one area of the sky are used to generate the local density maxima (or minima). This builds up a topological map of the dark matter distribution which can be compared to the topology based on a redshift survey when it is smoothed to the scale of the peculiar velocities.

The redshift sample that seems most suited for this purpose is that of a flux limited sample of IRAS galaxies (Strauss et al. 1992). IRAS galaxies are generally star forming spirals that are located in regions of modest to low galaxy density. The linchpin of this analysis is the explicit assumption that peculiar velocities are generated locally. Thus, a galaxy near a mass concentration such as the GA or the Coma cluster feels only that cluster. The LP result clearly calls this assumption into question as the scale over which peculiar velocities of individual galaxies is unclear. Thus, while the POTENT method when applied to the IRAS redshift sample does return a value of ₀ = 1, it remains unclear if a fair volume has been sampled.

Figure 4-6 shows the comparison between the density distribution as inferred from POTENT compared to that from the IRAS galaxy redshift survey. The qualitative agreement is good as both maps clearly reveal the Perseus-Pisces, Coma and Hydra-Centaurus regions which are the three nearest high density regions. It is, however, interesting to speculate that if large scale variations in dark matter densities exist, then galaxies located near the peaks of that distribution may have more dark matter phased mixed into their potentials than galaxies located near the valleys. This could introduce systematic error in the determination of relative distances and may be the source of systematic error in the LP result. We discuss this possibility a bit further in Chapter 5.

Figure 4-6: Comparison of density distributions inferred from the POTENT method to that obtained directly from a redshift survey of IRAS galaxies. Top panel shows the density distribution represented by contours. This figure has been adapted from Dekel 1994 (and also Strauss and Willick 1995). The heavy contour marks the boundary of the comparison volume of effective radius 46 Mpc/h The bottom panels show the contour view edge-on where the height in the surface plot is proportional to the density contrast. This figure comes courtesy of A. Dekel and will appear in Sigad etal 1997. In both cases the data have both smoothed with a Gaussian window of radius 12 Mpc/h . While the POTENT density field is more strongly peaked than the density field inferred from the IRAS data, the two representations are qualitiatively similar in that two principal density maxima in the Local Universe clearly stand out. These are associated with the Hydra-Cen and the Perseus-Pisces superclusters.

A lengthy but excellent review of the comparison between peculiar velocity data and gravitational instability plus CDM theory is offered by Strauss and Willick (1995). Their summary clearly shows that various attempts to measure through some 20 different methods, yield a range of values from 0.45 to 1.28, with no clearly preferred method dominating the measurements. Moreover, constraints on from peculiar velocity data seem to depend on scale (and choice of sample). For the simplest local system, the infall of the Local Group to the Virgo cluster, although the infall velocity is uncertain, low values of (e.g., 0.2-0.3) are supported. On larger scales, all-sky samples such as the IRAS galaxy sample of Fisher et al. (1994), when smoothed with a 1200 km s^-1 Gaussian, favors = 1.

From the observational point of view there are no strong constraints on . While the bulk of the data prefer values of 0.3, a highly dark matter dominated Universe (e.g., =1) can not be entirely ruled out. This leads to a physical divergence of cosmological models. On the one hand, the Universe might actually be relatively simple having most or all of its mass in conventional form (e.g., baryons). On the other hand, the Universe might be dominated by some exotic form of matter that we have not detected yet. Since its the mass distribution which determines the overall geometry of spacetime and hence our cosmological model, the solution of the dark matter problem clearly has far reaching implications. As we will now investigate in detail, there are strong and compelling theoretical reasons to believe that = 1 and that dark matter dominates the large scale behavior of the Universe.