


Elliptical galaxies are collisionless systems, in the sense that the forces between individual stars are unimportant compared with the mean gravitational field. Most elliptical galaxies are nevertheless smooth and relaxed in appearance, a puzzle first noted by Zwicky (1939). In statistical mechanics, the approach of macroscopic systems to a relaxed state is tied to the exponential instability of the motion of individual particles, i.e. to chaos ([Wightman 1971]; [Ford 1975]). In the case of a hard sphere gas, for instance, the chaos results from collisions between molecules which rapidly erase memory of the initial state ([Sinai 1963]). In galaxies, where close encounters between stars are rare, relaxation must be driven by some other mechanism that eliminates correlations. One candidate, discussed above, is the stochasticity associated with motion in non-axisymmetric potentials. Motion in rapidly-varying potentials is also likely to be complex and one expects relaxation under such conditions to be especially efficient. The term "mixing" is used by statistical physicists to describe all such forms of relaxation, both collisional and collisionless, in fixed as well as time-dependent potentials. Mixing can take place at various speeds and can even be arbitrarily slow; an example of slow mixing in galaxies is the persistence over many crossing times of narrow features like "shells" ([Quinn 1984]). However, in statistical mechanics, mixing is almost always assumed to be associated with chaos: in part because stochasticity is the norm in complex systems, and in part because quasiperiodic motion tends to preserve correlations for long times. The fact that most stars in elliptical galaxies are not associated with narrow features like shells suggests that chaotic mixing, or something similar, was active during galaxy formation.
The association of relaxation with exponential instability is not often made in the astronomical literature, where the emphasis has historically been on quasi-periodic motion. For instance, Jeans's (1915) theorem states that the distribution function of a relaxed galaxy must be expressible in terms of the integrals of motion, and his theorem has been interpreted as according a priveledged status to integrable potentials (e.g. [Binney 1982b]). Proofs of Jeans's theorem are sometimes based on the assumption that the potential is fully integrable (e.g. [Binney & Tremaine 1987], Appendix 4a). Statistical physicists, on the other hand, view integrals of the motion as impediments to relaxation and routinely associate chaos with a steady state. Similarly, discussions in the astronomical literature of relaxation in time-dependent potentials, or "violent relaxation" ([Lynden-Bell 1967]; [Shu 1978]), rarely focus on the mixing properties of the flow, even though such properties are considered basic for understanding the evolution of other many-particle systems like gases (Sinai 1979).
While there is merit in both points of view, the astronomer's traditional preoccupation with regular motion has been something of an impediment toward understanding collisionless relaxation. Regular orbits are the most useful building blocks for constructing self-consistent models, but it does not follow that integrability is a necessary condition for a steady state to exist; in fact, the redistribution of stars in phase space that drives relaxation is much easier to arrange when the motion is not quasi-periodic. Furthermore, to the extent that galactic potentials are integrable - and the work reviewed in the previous sections suggests that most elliptical galaxies may be close to axisymmetric, hence nearly integrable - a mechanism like chaotic mixing is probably required in order to explain how they got that way. It is likely too that our understanding of "violent relaxation" will be sharpened once attention is focussed on the properties of the phase-space flow that are responsible for driving evolution toward a steady state in time-dependent potentials.
Jeans (1915) noted that the phase space density of a collisionless stellar system satisfies the continuity equation
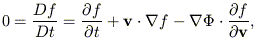
| (33) |
which states that f remains constant as one follows the motion of any star. In a steady state, ðf / ðt = 0, f must therefore be constant along trajectories at a given time, and one way to achieve this is by writing f as a function of the integrals of motion.
However not all integrals are valid arguments of f, as a number of
authors
([Kurth 1955];
[Contopoulos 1960];
[Lynden-Bell 1962b])
subsequently pointed out. The relative phase,
 i /
i /
 i -
i -
 j /
j /
 j,
between motion in different directions around an invariant torus is a
bona fide integral, but
allowing f to depend on it would yield a phase space density
with multiple values at a single point since trajectories
with different phases all fill the torus densely
(assuming incommensurability of the frequencies).
Integrals that do not have this property are called "isolating": an
isolating integral is one that, in some transformed coordinate
system, makes
ðH / ðpi a function only of the
coordinate conjugate to pi.
In an integrable system with N degrees of freedom, the
isolating integrals are the N actions or any set of N
independent functions of the actions.
Jeans's theorem for a galaxy in which the motion is fully
integrable becomes:
j,
between motion in different directions around an invariant torus is a
bona fide integral, but
allowing f to depend on it would yield a phase space density
with multiple values at a single point since trajectories
with different phases all fill the torus densely
(assuming incommensurability of the frequencies).
Integrals that do not have this property are called "isolating": an
isolating integral is one that, in some transformed coordinate
system, makes
ðH / ðpi a function only of the
coordinate conjugate to pi.
In an integrable system with N degrees of freedom, the
isolating integrals are the N actions or any set of N
independent functions of the actions.
Jeans's theorem for a galaxy in which the motion is fully
integrable becomes:
The phase space density of a stationary stellar system with a globally integrable potential can be expressed in terms of the isolating integrals in that potential.
An equivalent statement is that f is constant on every invariant torus.
A troublesome feature of Jeans's theorem when stated in this way is its apparent restriction to integrable systems, which must be vanishingly rare in nature. But as a number of authors, notably Pfenniger (1986) and Kandrup (1998b), have emphasized, regularity of the motion is in no way a prerequisite for a steady state to exist. The special status that Jeans's theorem seems to accord to integrable potentials disappears when one recognizes that the theorem is really a statement about phases, not about integrals: in a steady state, stars must be uniformly distributed with respect to angle over each invariant torus. In a region of phase space that is not integrable, stationarity can likewise be achieved by requiring f to be constant throughout the region: since f is conserved following the flow, an initially constant value will remain constant forever. The generalization of Jeans's theorem to general, non-integrable potentials is then:
The phase space density of a stationary stellar system must be constant within every well-connected region.
A well-connected region is one that can not be decomposed into two finite regions such that all trajectories lie in either one or the other (what mathematicians call "metric transitivity.") Invariant tori are such regions, but so are the more complex parts of phase space associated with stochastic trajectories.
An example of a well-connected region that is not an invariant torus is the "Arnold web," the phase space region accessible to every stochastic trajectory at a given energy in a 3 DOF system ([Lichtenberg & Lieberman 1992]). Every point in the Arnold web has the same energy, hence a constant f within such a region could formally be written as f = f (E) as in Jeans's original formulation. However there will generally exist invariant tori at the same energy on which the motion respects two additional integrals and where f has different values. The phase space density in such a system is therefore likely to be an extremely complicated function of the coordinates.
In weakly chaotic potentials, the time required for a single trajectory to visit the entire Arnold web may be very long, (5) and one would not expect the distribution of stars in stochastic phase space to have reached a uniform value in a galaxy lifetime. In such potentials, chaotic trajectories mimic regular orbits with effective integrals for many oscillations. In more strongly chaotic potentials, one can define time-independent mass components that correspond to an approximately uniform filling of stochastic phase space at every energy. Such components have shapes that are not very useful for reconstructing a galaxy's figure; nevertheless they can constitute a significant fraction of the mass of a self-consistent model ([Kaufmann & Contopoulos 1996]; [Merritt & Fridman 1996]), and there is every reason to believe that nature uses such components as well.
In a 2 DOF system, the stochastic regions at a given energy are separated by the invariant tori. This is the case in axisymmetric potentials, where f can have different values in different stochastic regions at a given E and Lz. Axisymmetric models with this level of generality have yet to be constructed. The classical approach of writing f = f (E, Lz) for an axisymmetric galaxy assigns a constant density to every point on hypersurfaces of constant E and Lz. Since some of these points correspond to stochastic orbits in general, the two-integral approach to axisymmetric modelling actually depends on the more general form of Jeans's theorem given above for its justification.
5.2. Approach to a Steady State
The evolution of a collisionless ensemble of stars is never toward the uniform population of phase space demanded by Jeans's theorem. An initially compact group of phase points gets drawn out into a filament of ever decreasing width, a consequence of the conservation of phase space volume implied by Liouville's theorem. Observed with infinite resolution, the region occupied by these points becomes increasingly striated, not more uniform. The most that can be hoped for is that the coarse-grained phase space density will approach a constant value within some region. However even this outcome is not guaranteed by any very general property of Hamilton's equations. For instance, an ensemble of points on an invariant torus does not evolve toward a coarse-grained steady state - it simply translates, unchanged, around the torus.
The simplest model for collisionless relaxation is "phase mixing," the gradual shearing of points in a fixed, integrable potential (Figure 10a). Since the fundamental frequencies of regular motion are generally different on different tori, two points that lie on adjacent tori will separate linearly with time. After many revolutions, the density of stars in this filament, averaged over a finite phase-space volume, will be independent of angle. Thus the coarse-grained density evolves asymptotically to a state that satisfies Jeans's theorem, in spite of the fact that the fine-grained density never reaches a steady state.
|
Figure 10. (a) Phase mixing vs. (b) chaotic mixing. Both types of mixing produce evolution toward a state such that the coarse-grained phase space density is uniform within some region. In phase mixing, the separation between two initially nearby points increases approximately linearly with time, while in chaotic mixing the separation increases exponentially on average. Although the two types of mixing are normally defined in fixed potentials, qualitatively similar evolution of both sorts occurs in time-dependent potentials as well; an example is shown in Figure 12. |
This coincidence is a consequence of the ergodicity of regular motion. Ergodic motion spends equal amounts of time, on average, in equal phase-space volumes (defined with respect to the invariant measure). Ergodicity is a non-trivial property which can only be rigorously proved for certain classes of motion. Regular motion is ergodic due to its quasi-periodicity: since the angles on the torus increase linearly with time, any trajectory fills the torus uniformly and densely in a time-averaged sense. This time-averaged uniformity with respect to angle guarantees that phase mixing will tend toward a coarse-grained state in which no angle is preferred.
Ergodicity by itself is a condition only on the time-averaged behavior of a trajectory. Relaxation implies more in general: not only should the entire past of a given phase point cover the phase space uniformly, but so also should the present of any neighborhood of the original point. In other words, a small patch of phase space should evolve in such a way that it uniformly covers, at a single later time, a much larger region (Figure 10b). This process, which dynamicists call simply "mixing," can occur in many ways and at various speeds, but it is most commonly associated with the exponential instability of stochastic motion, and the term "chaotic mixing" will be used here where there is danger of confusion with phase mixing. Krylov (1979) was the first to emphasize the role of chaotic mixing in explaining relaxation processes in statistical mechanics, and nowadays chaotic mixing is regarded by statistical physicists as essentially equivalent to relaxation ([Sinai 1979]).
Since chaotic mixing is driven by the exponential instability of the
motion, it occurs locally at a rate that is determined by the
Liapunov exponents.
It is also irreversible, in the sense that an infinitely precise
fine-tuning of the velocities would be required in order
to undo its effects. Phase mixing is reversible, and it
has no well-defined time scale:
the rate at which a group of phase points shears depends on the
range of orbital frequencies in the group.
If the maximum and minimum frequencies are
 1 and
1 and
 2 respectively,
one expects phase mixing to take place on a time scale of order
(
2 respectively,
one expects phase mixing to take place on a time scale of order
( 1 -
1 -
 2)-1.
This time scale is never less than a dynamical time and can be much
longer; for points restricted to a single torus, the time scale
is infinite and no phase mixing occurs.
2)-1.
This time scale is never less than a dynamical time and can be much
longer; for points restricted to a single torus, the time scale
is infinite and no phase mixing occurs.
Phase mixing and chaotic mixing are idealizations of the mixing that takes place in real galaxies, whose potentials may vary with time in complex ways. Nevertheless one often sees, in time-dependent numerical simulations, examples of mixing that are readily identified with these two basic types. An example, discussed below, is illustrated in Figure 12.
5.2.2. Mixing in Fixed Potentials
Stochastic motion is nearly random in the sense that the likelihood of finding a particle anywhere in the stochastic region tends toward a constant value after a sufficiently long time. An initially compact group of stars should therefore spread out until it covers the accessible phase space uniformly in a coarse-grained sense. Kandrup and collaborators ([Kandrup & Mahon 1994]; [Mahon et al. 1995]) first investigated this process in the context of galactic dynamics. They focussed on motion in two-dimensional potentials, integrating ensembles of initially localized points until they had reached nearly invariant distributions. They found that the coarse-grained distribution function typically exhibited an exponential approach toward equilibrium at a rate that correlated well with the mean Liapunov exponent for the ensemble. When evolved for much longer times, f was found to slowly change as orbits diffused into regions that, although accessible, were avoided over the shorter time interval. Kandrup et al. suggested that one could construct approximately steady-state models of galaxies using the near-invariant distributions, since the time scale for the slower evolution was typically much longer than a galaxy lifetime.
Similar calculations in three dimensions
were carried out in the "imperfect ellipsoid" potential by
Merritt & Valluri
(1996)
(Figure 11).
Ensembles of particles were evolved starting from small patches
on the equipotential surface, initial conditions that would
have generated box orbits in an integrable potential.
Merritt & Valluri also found an initially rapid approach to a
near-invariant distribution followed by a slower evolution.
Ensembles with starting points near the y - z instability
strip (Figure 3) exhibited the most
rapid mixing, with e-folding times
of only ~ 10 crossing times in models with small core radii
m0 or with central point masses containing
 0.1%
of the total mass.
Ensembles started near regions where the motion was regular
evolved more slowly, a consequence of the "stickiness" of invariant tori.
Merritt & Valluri suggested that chaotic mixing would tend to
axisymmetrize at least the central regions of triaxial galaxies
with high central concentrations or massive nuclear black holes.
0.1%
of the total mass.
Ensembles started near regions where the motion was regular
evolved more slowly, a consequence of the "stickiness" of invariant tori.
Merritt & Valluri suggested that chaotic mixing would tend to
axisymmetrize at least the central regions of triaxial galaxies
with high central concentrations or massive nuclear black holes.
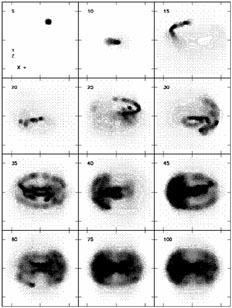
|
Figure 11. An example of chaotic mixing in a fixed triaxial potential (Merritt & Valluri 1996). An ensemble of 104 isoenergetic particles move independently in the time-dependent gravitational field generated by the Imperfect Ellipsoid with m0 = 0.01. Each frame is labelled by the elapsed time in units of the period of the long-axis orbit; the particles are seen in projection against the x - z plane. After ~ 100 orbital periods, the particles have reached a nearly stationary, coarse-grained state. This example suggests the way in which time-independent density components exist even in potentials that are not characterized by integrals of the motion aside from the energy. |
Kandrup (1998a) compared the efficiency of phase mixing and chaotic mixing in 2D and 3D potentials. He noted that - for initially very localized ensembles - the two processes occur at very different rates: chaotic mixing takes place on the Liapunov, or exponential divergence, time scale while the phase mixing rate falls to zero. But phase mixing of a group of points with a finite extent can be much more rapid. Furthermore the mixing rate of chaotic ensembles typically falls below the Liapunov rate once the trajectories separate; this is especially true for those stochastic orbits that are confined over long periods of time to restricted parts of phase space. The effective rates of phase mixing and chaotic mixing might therefore be comparable in real galaxies. Kandrup noted also that chaotic mixing in 3D potentials can occur at substantially different rates in different directions.
Smooth potentials are idealizations of real elliptical galaxies,
which sometimes contain imbedded disks, shells, or other fine
structure. As seen by a single star, these distortions would add
small-amplitude perturbing forces to the mean field.
Such perturbations would not be expected to have much consequence
for either strongly chaotic or nearly regular orbits, but they
might have an appreciable effect on the evolution of weakly stochastic
orbits, by scattering trajectories away from a trapped region into a
region where mixing is more rapid.
Goodman &
Schwarzschild (1981)
found that small perturbations had
relatively little effect on the behavior of stochastic orbits in their
nearly-integrable triaxial model. Habib, Kandrup & Mahon
(1996,
1997)
observed much more striking
effects of noise on the evolution of trapped stochastic orbits
in two dimensionial potentials.
These authors found that even very weak noise, with
a characteristic time scale
| 1 / v
5.2.3. Mixing in Time-Dependent
Potentials
In a real galaxy, the approach to a stationary state takes place
against the backdrop of a time-varying potential.
King (1962),
Hénon (1964),
Lynden-Bell (1967)
and others realized that relaxation
under such conditions might be very efficient, and the latter
author made the bold suggestion that the relaxation rate could be
directly identified with the rate of change of a star's
potential energy. Lynden-Bell proposed that the time scale for
"violent relaxation" was
with
A rearrangement of stars in energy space can only take place if the
potential is time-dependent.
But in other respects, the identification of
ð
Mixing that is driven by changes in the mean-field potential
is self-limiting in the sense that the potential approaches
a steady state as the mixing progresses.
The effectiveness of "violent relaxation" therefore depends
strongly on how long the mixing is able to continue, hence on
the initial conditions.
A number of numerical simulations have borne this out.
Hoffman, Shlosman
& Shaviv (1979)
followed the collapse and
relaxation of a spherical galaxy starting from two initial states
with different values of the "virial ratio" | 2T/W|, where
T and W are the initial kinetic and potential energies.
For | 2T / W| = 0.49 they found a deeper collapse than for
| 2T / W = 0.59|, but the subsequent decay of the virial
ratio to its equilibrium value of 1 was also more rapid, thus allowing
less time for the mixing to take place. Van Albada and May
([van Albada 1982];
[May & van Albada
1984])
simulated the evolution of initially "cold" clouds with
irregular shapes and clumpy particle distributions.
They found that the degree of relaxation - as measured, for
instance, by the change in the binding energy distribution -
was well correlated with the initial degree of irregularity.
They argued that clumpy initial conditions were effective at
driving relaxation since they permitted the mixing to continue
for a prolonged period of time.
Villumsen (1984)
carried out similar experiments starting from
spherical as well as highly flattened initial conditions.
He too noted the greater complexity of the motion in the
nonspherical collapses and he argued that this complexity was
necessary if the evolving galaxy was to lose memory of its
initial state. Similar conclusions were reached by
McGlynn (1984)
and by
Londrillo, Messina
& Stiavelli (1991).
The view of relaxation in a time-dependent potential as a
self-limiting process was incorporated into a heuristic model by
Wiechen, Ziegler and collaborators
([Wiechen, Ziegler
& Schindler 1988];
[Ziegler & Wiechen
1989];
[Stahl, Ziegler &
Wiechen 1990];
[Ziegler & Wiechen
1990]).
These authors assumed that the degree to which an
out-of-equilibrium stellar system relaxes could be estimated
by comparing it to a reference system, the "lowest energy
state," defined in the following way.
Starting from the initial state, they rearranged the matter in phase
space so as to minimize the total energy; in other
words, they required the largest values of f to coincide with the
most negative values of
h = v2/2 +
Nozakura (1992)
applied Wiechen & Ziegler's algorithm to the
spherical initial states considered by
van Albada (1982)
in his N-body simulations.
Nozakura found that the formalism was useful for predicting the final
state when the initial state was only moderately far from
equilibrium, with a virial ratio
2T / |W|
Figure 12. Evolution of a
spherically-symmetric system of particles in (r,
vr) phase space starting with zero velocity and
An interesting illustration of mixing in a time-dependent
potential was presented by
Henriksen & Widrow
(1997).
These authors simulated spherically-symmetric
collapses of "cold" particle distributions with power-law density
profiles,
Mixing in a time-dependent potential allows the energies of stars
to change, and if the mixing is very efficient or prolonged, one
might expect the distribution of energies to approach a "most
probable" state.
Much the same thing takes place in a gas, where collisions
between molecules imply a rapid exchange of kinetic energies;
the most probable distribution of particle energies
is obtained by maximizing the entropy, leading to the
well-known Maxwell-Boltzmann velocity distribution.
One can carry out a similar calculation for stellar systems
([Ogorodnikov 1965];
[Lynden-Bell 1967];
[Shu 1978]),
with the not-very-surprising result that the velocity distribution
should be Maxwellian in this case as well. However the self-consistent
model corresponding to a Maxwellian velocity distribution,
the isothermal sphere, has an infinite radius and mass.
One might interpret this to mean that
the phase-space structure of a real galaxy should be
similar in some respects to that of an isothermal sphere,
but the entropy arguments give little indication of
precisely what the similarities should be.
A number of authors have nevertheless attempted to
use entropy arguments to draw conclusions about the end
state of collisionless relaxation
([Tremaine, Hénon
& Lynden-Bell 1986];
[Madsen 1987];
[White & Narayan
1987];
[Mathur 1988];
[Spergel &
Hernquist 1992];
[Soaker 1996]).
In addition to the difficulty just mentioned,
these studies must deal with the fact that
the equilibrium state of a stellar system depends strongly on
the initial conditions.
If the correct final state is to be singled out by an entropy
maximization, the dependence of the final state on the initial
state must somehow be translated into a set of constraints.
Inferring the final state then becomes equivalent to specifying
these constraints.
There is currently no clear understanding of how this can be done
and it is not even certain that the exercise would be physically
enlightening.
An illustration of the subtleties associated with entropy
arguments is the controversy surrounding the study of
Tremaine, Lynden-Bell
& Hénon (1986).
These authors noted, following
Tolman (1938),
that any functional of the form
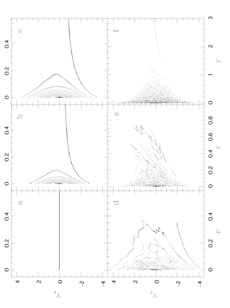
is precisely conserved during collisionless evolution;
here C(f ) is any "convex" function of f,
d2C / df2
One is tempted to conclude that SC is a
monotonically increasing function of time and that any
such functional can play the role of an entropy.
Such a conclusion was rejected by a number of authors
([Binney 1987];
[Dejonghe 1987];
[Kandrup 1987];
[Sridhar 1987])
on the following grounds.
Identifying the initial state with the fine-grained f is
equivalent to assuming that the initial state is known with
infinite precision.
The increase in SC is then a consequence
of the coarse-graining: at any time, the coarse-grained
SC is
greater than the fine-grained SC, hence
SC(t2) >
SC(t1).
But it does not follow that SC is monotonically
increasing and it might well decrease.
In fact, equation (36) is true irrespective of whether
t2 is greater or less than t1.
Entropy increases of a physically interesting sort are always
associated with irreversibility, that is with chaos
([Ruelle 1991]),
and it is remarkable that so few discussions of entropy in the
galactic dynamics literature have paid any attention to the
dynamical properties of the phase-space flow.
Chaotic mixing in a fixed potential, as illustrated in
Figure 11,
represents a true entropy increase in the sense understood by
Boltzmann, and the irreversibility observed in numerical
simulations of "violent relaxation" (e.g.
Figure 12)
suggests that something very similar takes place in time-dependent
potentials as well.
It is in this direction that a fuller understanding of
collisionless relaxation probably lies.
The irreversibility of mixing flows like the one illustrated in
Figure 11 implies a reduction in the effective
number of orbits:
all the stochastic trajectories at a given energy are gradually
replaced by a single invariant ensemble, whose shape is typically
not well matched to that of the galaxy.
If time scales for chaotic mixing are comparable to galaxy
lifetimes, this reduction might be expected to encourage a galaxy to
evolve away from a triaxial shape toward a more axisymmetric one,
in which most of the orbits are tubes that avoid the destabilizing center.
A pioneering study of mixing-induced evolution was carried out by
Norman, May & van
Albada (1985),
who performed N-body
integrations of triaxial models in which a central compact object
was slowly grown.
They found a modest degree of evolution toward more spherical
shapes near the center.
Norman et al.'s simulations were intended to represent the effect of a
massive nuclear black hole on the surrounding galaxy; however,
because of computational limitations, they were forced to adopt a
softening length for the central object that was close to the
gravitational radius of influence
rh ~ GMh /
A natural way to increase the central density of a galaxy
model is through the inclusion of a dissipative component which
accumulates near the center as its energy and angular momentum are
carried away.
N-body studies of galaxy formation that include such a
component often reveal an evolution toward more
axisymmetric shapes as the central mass grows.
Katz & Gunn (1991)
carried out such simulations
starting from initial conditions containing either no "gas,"
or a 10 : 1 ratio of "stellar" to "gas" particles.
Initially the two components were well mixed; however the gas
particles quickly accumulated near the center where they formed a
disk. In the absence of a dissipative component, the stellar particles
in these simulations relaxed into strongly triaxial shapes, with
typical axis ratios of ~ 1 : 0.7 : 0.5.
When gas was included, the final stellar distribution was
found to always be nearly oblate-axisymmetric, with
b/a
Barnes (1992,
1996)
reported the results of N-body simulations of
mergers between disk galaxies with and without a
dissipative component.
In the absence of gas, the remnants acquired shapes that
depended strongly on the initial orientations and impact
parameter of the colliding disks; many of the remnants were
strongly triaxial.
When as little as 1.5% of the total mass was added in the form of
dissipative particles, the remnants acquired much more axisymmetric
shapes.
Barnes (1996)
cataloged the stellar orbits in the remnants and
found a preponderance of short-axis tubes in the remnants
containing gas, as expected for nearly axisymmetric potentials.
Barnes & Hernquist
(1996)
confirmed these results with further
simulations and noted that the final shapes of the remnants were
well correlated with the depth of the central potential.
They speculated that the evolution toward oblate figures was
driven largely by the destabilization of box orbits moving in the
deepened potential, i.e. by chaotic mixing.
The effect of a massive central singularity on the structure of an
initially triaxial galaxy was studied by
Merritt & Quinlan
(1998)
using an N-body code with much higher spatial and temporal
resolution than in the pioneering simulation of Norman et al.
The final shape achieved by their model after growth of the
black hole was nearly spherical at the center and close
to axisymmetric throughout; the rate of change of the
galaxy's shape depended strongly on the ratio
Mh/Mg of black hole mass to galaxy mass.
When Mh/Mg was less than about 0.3%,
the galaxy evolved
in shape over ~ 102 orbital periods, while increasing
Mh/Mg to 3% caused the galaxy to become
axisymmetric in little more than a crossing time.
Merritt & Quinlan proposed that the rapid evolution toward
axisymmetric shapes for Mh/Mg
Chaotic mixing induced by a central density cusp or nuclear black
hole could have a number of other consequences for the structure
of elliptical galaxies and bulges
([Merritt 1998]).
Elliptical galaxies with nonsmooth phase space populations are
expected to be "boxy" or peanut-shaped, since individual
orbits, both boxes and tubes, are strongly dimpled when seen in
projection
([Binney & Petrou
1985]).
The fact that most elliptical galaxies have accurately elliptical
isophotes suggests that some process has acted to smooth the
distribution of orbital turning points at every energy.
"Violent relaxation" is one candidate for this smoothing
process, but it is apparently not effective enough, since the
end-products of N-body simulations are often strongly
peanut-shaped (e.g.
[May, van Albada &
Norman 1985];
[Quinn & Goodman
1986];
[Udry 1993];
[Ziegler, Wiechen
& Arendt 1994]).
An alternative mehcanism is chaotic mixing induced by a central
black hole;
Merritt & Quinlan
(1998)
noted that the
growth of a central mass concentration converts boxy, triaxial
systems into axisymmetric ones with accurately elliptical
isophotes.
This result may explain the observed correlation between boxiness and
kinematical measures of triaxiality
([Kormendy &
Bender 1996]).
On a deeper level, the distribution function of an axisymmetric
galaxy formed in this way would be biased toward forms for f
that are as nearly constant as possible, i.e. which do not
depend strongly on a third integral.
Detailed modelling of M32, a galaxy that is old compared to
expected time scales of chaotic mixing, in fact suggests a best-fit
f
5 The more relevant time scale is the
chaotic mixing time, defined below.
Back.

 t |-1 of
order 106 crossing times, could
induce substantial changes in the motion of trapped stochastic
orbits over ~ 102 periods.
Merritt & Valluri
(1996)
also considered the effect of noise
on chaotic mixing in triaxial potentials.
They observed a significant enhancement in the mixing rate of
trapped ensembles for noise with a characteristic time scale
of ~ 103 orbital periods.
These results suggest that chaotic mixing in strongly
time-dependent potentials, like those associated with a
collapsing protogalaxy, might be much more efficient than in
experiments based on fixed potentials.
t |-1 of
order 106 crossing times, could
induce substantial changes in the motion of trapped stochastic
orbits over ~ 102 periods.
Merritt & Valluri
(1996)
also considered the effect of noise
on chaotic mixing in triaxial potentials.
They observed a significant enhancement in the mixing rate of
trapped ensembles for noise with a characteristic time scale
of ~ 103 orbital periods.
These results suggest that chaotic mixing in strongly
time-dependent potentials, like those associated with a
collapsing protogalaxy, might be much more efficient than in
experiments based on fixed potentials.
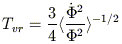
(34)
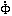 the time derivative
of the gravitational potential.
For a collapsing sphere, Lynden-Bell noted that Tvr
was similar to the collapse time, consistent with
N-body simulations which showed nearly complete relaxation
after just a few radial oscillations.
the time derivative
of the gravitational potential.
For a collapsing sphere, Lynden-Bell noted that Tvr
was similar to the collapse time, consistent with
N-body simulations which showed nearly complete relaxation
after just a few radial oscillations.
 / ðt
with a relaxation rate is problematic.
Instantaneous changes in the potential imply only a relabelling
of particle energies, not necessarily a divergence of
phase space trajectories or a redistribution of energies, which
are also prerequisites for relaxation.
It is in fact possible to construct oscillating
models which exhibit no tendency to relax
([Louis & Gerhard
1988];
[Sridhar 1989];
[Sridhar &
Nityananda 1989];
[Mineau, Feix &
Rouet 1990]).
The failure of these models to reach a steady state
is a result of their being constructed
in such a way that mixing is inhibited;
thus the distribution of particle energies does not relax
even though the energy of individual particles is constantly changing.
For instance, in
Sridhar's (1989)
pulsating models, all of the stars move with the same fixed frequencies
and no mixing can occur.
Such examples are artificial but demonstrate that mixing is
no less a prerequisite for relaxation in time-dependent potentials
than it is in fixed potentials.
Potential fluctuations would be expected to promote relaxation
only to the extent that they encourage mixing.
/ ðt
with a relaxation rate is problematic.
Instantaneous changes in the potential imply only a relabelling
of particle energies, not necessarily a divergence of
phase space trajectories or a redistribution of energies, which
are also prerequisites for relaxation.
It is in fact possible to construct oscillating
models which exhibit no tendency to relax
([Louis & Gerhard
1988];
[Sridhar 1989];
[Sridhar &
Nityananda 1989];
[Mineau, Feix &
Rouet 1990]).
The failure of these models to reach a steady state
is a result of their being constructed
in such a way that mixing is inhibited;
thus the distribution of particle energies does not relax
even though the energy of individual particles is constantly changing.
For instance, in
Sridhar's (1989)
pulsating models, all of the stars move with the same fixed frequencies
and no mixing can occur.
Such examples are artificial but demonstrate that mixing is
no less a prerequisite for relaxation in time-dependent potentials
than it is in fixed potentials.
Potential fluctuations would be expected to promote relaxation
only to the extent that they encourage mixing.
 and vice versa.
At the same time, they required that Liouville's theorem be satisfied, i.e.
that the volume of each element of phase space be conserved.
Wiechen, Ziegler &
Schindler (1988)
showed that such a "lowest
energy state" could always be uniquely defined.
This state is however unreachable, since its energy is (by
definition) different from that of the initial state. But
Ziegler & Wiechen
(1989)
suggested that the energy difference
between the initial and lowest-energy states
could be taken as a measure of the degree to which the
potential would evolve before the mixing came to a halt.
They then simulated the mixing process by applying a smoothing
operator to the initial state,
after demonstrating that the smoothing process always
increases the total energy by making the distribution of
matter less compact.
They therefore chose the smoothing length such that
the reference model corresponding to the smoothed initial distribution
had the same energy as the unsmoothed initial state.
Finally they identified this smoothed, lowest energy state with the
equilibrium configuration.
Ziegler & Wiechen
(1989)
applied their formalism to a single,
spherical initial state and found good agreement with
a full numerical simulation.
and vice versa.
At the same time, they required that Liouville's theorem be satisfied, i.e.
that the volume of each element of phase space be conserved.
Wiechen, Ziegler &
Schindler (1988)
showed that such a "lowest
energy state" could always be uniquely defined.
This state is however unreachable, since its energy is (by
definition) different from that of the initial state. But
Ziegler & Wiechen
(1989)
suggested that the energy difference
between the initial and lowest-energy states
could be taken as a measure of the degree to which the
potential would evolve before the mixing came to a halt.
They then simulated the mixing process by applying a smoothing
operator to the initial state,
after demonstrating that the smoothing process always
increases the total energy by making the distribution of
matter less compact.
They therefore chose the smoothing length such that
the reference model corresponding to the smoothed initial distribution
had the same energy as the unsmoothed initial state.
Finally they identified this smoothed, lowest energy state with the
equilibrium configuration.
Ziegler & Wiechen
(1989)
applied their formalism to a single,
spherical initial state and found good agreement with
a full numerical simulation.
 0.5, but that the agreement was poor for stronger collapses.
Ziegler, Wiechen &
Arendt (1994)
argued that the mixing in
strong collapses was "non-uniform," i.e. that the appropriate
smoothing length to apply to particles in the (final) core and
halo should be different.
Lacking a detailed understanding of the evolution, however, they were
unable to specify how the smoothing length should vary with position.
They noted also that the tendency of initially spherical models
to acquire highly elongated shapes during the collapse
([Merritt &
Aguilar 1985];
[Aguilar & Merritt
1990];
[Canizzo &
Hollister 1992])
had no natural explanation in their model.
0.5, but that the agreement was poor for stronger collapses.
Ziegler, Wiechen &
Arendt (1994)
argued that the mixing in
strong collapses was "non-uniform," i.e. that the appropriate
smoothing length to apply to particles in the (final) core and
halo should be different.
Lacking a detailed understanding of the evolution, however, they were
unable to specify how the smoothing length should vary with position.
They noted also that the tendency of initially spherical models
to acquire highly elongated shapes during the collapse
([Merritt &
Aguilar 1985];
[Aguilar & Merritt
1990];
[Canizzo &
Hollister 1992])
had no natural explanation in their model.

 r-3/2
(Henriksen &
Widrow 1997).
The initial evolution is similar to
phase mixing in spite of the rapidly varying potential;
after a certain point, the motion undergoes a transition to
a more chaotic flow, allowing rapid
mixing between particles on neighboring phase-space streams.
This example shows that the distinction made in
Figure 10,
between phase mixing and chaotic mixing in a fixed potential, is
qualitatively valid in time-dependent potentials as well.
r-3/2
(Henriksen &
Widrow 1997).
The initial evolution is similar to
phase mixing in spite of the rapidly varying potential;
after a certain point, the motion undergoes a transition to
a more chaotic flow, allowing rapid
mixing between particles on neighboring phase-space streams.
This example shows that the distinction made in
Figure 10,
between phase mixing and chaotic mixing in a fixed potential, is
qualitatively valid in time-dependent potentials as well.
 ~
r-
~
r- ,
0 <
,
0 <  < 3.
The initial evolution was found to be essentially similar to
phase mixing, in spite of the rapidly varying potential: the
single phase-space thread corresponding to the initial model
became more and more tightly wound as the sphere oscillated
(Figure 12).
After a certain point, however, the motion underwent a transition to
a more complex flow, which allowed rapid
mixing between particles on neighboring phase-space streams.
While highly idealized, Henriksen & Widrow's simulations provide a
striking illustration of the way in which the efficiency of
relaxation is tied more to the complexity of the phase-space flow
than to the rate of change of the potential.
< 3.
The initial evolution was found to be essentially similar to
phase mixing, in spite of the rapidly varying potential: the
single phase-space thread corresponding to the initial model
became more and more tightly wound as the sphere oscillated
(Figure 12).
After a certain point, however, the motion underwent a transition to
a more complex flow, which allowed rapid
mixing between particles on neighboring phase-space streams.
While highly idealized, Henriksen & Widrow's simulations provide a
striking illustration of the way in which the efficiency of
relaxation is tied more to the complexity of the phase-space flow
than to the rate of change of the potential.
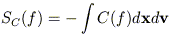
(35)
 0.
The constancy of SC is a result of the detailed
conservation of phase space volume implied by Liouville's theorem.
However if one computes SC at some time
t2 using a
coarse-grained approximation to f, and compares it to the value
of SC computed at an earlier time t1
using the exact f, one finds
0.
The constancy of SC is a result of the detailed
conservation of phase space volume implied by Liouville's theorem.
However if one computes SC at some time
t2 using a
coarse-grained approximation to f, and compares it to the value
of SC computed at an earlier time t1
using the exact f, one finds
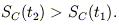
(36)
 2 of a true point
mass. In addition, their initial models were chosen to be close to
axisymmetric. As Norman et al. noted, both of these factors would tend
to limit the evolution, the first by eliminating large-angle
scattering of trajectories by the central object, the second by
reducing the fraction of stars on boxlike orbits that could pass
near the center.
2 of a true point
mass. In addition, their initial models were chosen to be close to
axisymmetric. As Norman et al. noted, both of these factors would tend
to limit the evolution, the first by eliminating large-angle
scattering of trajectories by the central object, the second by
reducing the fraction of stars on boxlike orbits that could pass
near the center.
 0.9.
The short-to-long axis ratio was nearly unchanged.
Udry (1993)
simulated dissipation in
triaxial galaxy models by a number of schemes:
including an ad hoc drag force on 10% of the particles;
adding a central particle containing 2.5% of the stellar mass;
or including a centrally concentrated distribution of particles containing
5% or 10% of the total mass.
While the simulations without "dissipation" resulted in
models with a range of triaxialities, the simulations including
dissipation evolved to nearly axisymmetric shapes, with
0.7
0.9.
The short-to-long axis ratio was nearly unchanged.
Udry (1993)
simulated dissipation in
triaxial galaxy models by a number of schemes:
including an ad hoc drag force on 10% of the particles;
adding a central particle containing 2.5% of the stellar mass;
or including a centrally concentrated distribution of particles containing
5% or 10% of the total mass.
While the simulations without "dissipation" resulted in
models with a range of triaxialities, the simulations including
dissipation evolved to nearly axisymmetric shapes, with
0.7  b/a
b/a
 1.
Dubinski (1994)
simulated dissipative infall inside an initially
triaxial halo by slowly increasing the mass associated
with a central, fixed component having either a spherical or
disklike shape.
The final mass of this central object was ~ 5% the mass of
the surrounding halo; however its scale length was large, roughly 0.1
that of the halo.
Dubinski nevertheless found a modest increase in the
intermediate-to-long axis ratio of the halo, from ~ 0.6 to ~ 0.8, with
less change in c/a.
1.
Dubinski (1994)
simulated dissipative infall inside an initially
triaxial halo by slowly increasing the mass associated
with a central, fixed component having either a spherical or
disklike shape.
The final mass of this central object was ~ 5% the mass of
the surrounding halo; however its scale length was large, roughly 0.1
that of the halo.
Dubinski nevertheless found a modest increase in the
intermediate-to-long axis ratio of the halo, from ~ 0.6 to ~ 0.8, with
less change in c/a.
 2.5% would tend to
cut off the supply of fuel to a growing black hole, thus imposing an upper
limit to its mass.
2.5% would tend to
cut off the supply of fuel to a growing black hole, thus imposing an upper
limit to its mass.
 f
(E, Lz)
([van der Marel et
al. 1998]).
f
(E, Lz)
([van der Marel et
al. 1998]).