6. COLLECTIVE INSTABILITIES

The chaotic mixing discussed in the previous section is driven by the exponential instability of stochastic motion; the effect of such mixing is typically to erase a density perturbation by spreading particles in phase space. However it is possible for a density perturbation to grow by inducing motion that reinforces the original overdensity. Such collective instabilities typically require the unperturbed motion to be highly correlated and they have been most thoroughly studied in thin disks, which are subject to a variety of unstable modes when sufficiently "cold" ([Sellwood & Wilkinson 1993]). In elliptical galaxies, where the stellar motions are more nearly random in direction, a perturbation in the density might be expected to rapidly attenuate as the stars move along their respective orbits. However it turns out that the motion in a variety of physically reasonable models is sufficiently correlated to induce growing modes.

The simplest model for an elliptical galaxy is a sphere in which the stellar velocities are isotropic, f = f (E). Antonov (1960, 1962) established a necessary and sufficient condition for linear stability of spherical systems satisfying df /dE < 0, in the form of a complicated variational principle. He went on to derive a number of simpler, sufficient conditions for stability. The most important of these are:

1. A spherical system with f = f (E) and df /dE < 0 is stable to all non-radial (i.e. non-spherically-symmetric) perturbations.

2. A spherical system with f = f (E), df / dE < 0 and d³ / d³ 0 is stable to all perturbations.

Antonov was able to show that the family of "stellar dynamical polytropes" defined by

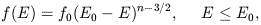
(37)

is stable for n 3/2, i.e. for all values of n such that df /dE 0. Antonov's second theorem was generalized by Doremus, Feix & Baumann (1971), Sygnet et al. (1984) and Kandrup & Sygnet (1985) to include any spherical system with df /dE < 0. This result may be used to verify that many of the isotropic models that resemble real galaxies are linearly stable.

A number of attempts have been made to generalize Antonov's theorems to spherical systems with anisotropic velocities, f = f (E, L²). One such generalization follows directly from Theorem II above: stability to radial perturbations is guaranteed if (ð / ð E*)² _E*⁰ f(E, L²) dE / (E - E*) < 0 ([Dejonghe & Merritt 1988]). Theorems of an even more general nature have been proposed, but their validity is not always clear. Dorémus & Feix (1973) and Gillon, Doremus & Baumann (1976) analyzed a "water bag" model for spherical stellar systems, in which the distribution function is represented as a set of bags of incompressible fluid; a perturbation is interpreted as a change in the volumes of the bags rather than as a change in the numerical value of the distribution function. They found stability to radial perturbations when ðf / ðE < 0 and stability to all perturbations when ðf / ðL < 0 as well. The former result was confirmed by Kandrup & Sygnet (1985) and Perez & Aly (1996), but the latter result would seem to definitely contradict numerical studies of the radial-orbit instability described below (Section 6.2); in fact Perez & Aly were able to find an error in the Gillon et al. proof. A criterion proposed by Hjorth (1994) for stability of a certain class of anisotropic models is also inconsistent with numerical results ([Meza & Zamorano 1997]).

As an alternative to proving theorems on stability, one can use physical intuition to search for particular, unstable models. This approach has been extremely successful, leading to the identification of several types of unstable behavior in models of hot stellar systems. Results on four such instabilities are reviewed below, roughly in the order in which their importance was first recognized. The first is a pulsational instability of spherical systems, first reported by Hénon (1973). The second is the radial-orbit instability, postulated by Antonov (1973) and observed by Polyachenko (1981). Third are bending instabilities, described as early as 1966 by Toomre in the context of disks, and observed in a number of N-body studies starting around 1990. Finally, instabilities in slowly-rotating oblate models with nearly circular orbits are discussed; these instabilities were first noticed in disk models and later seen in oblate spheroids.

6.1. Hénon's instability

Antonov's proofs leave open the question of the stability of systems with anisotropic or non-monotonic distribution functions. Hénon (1973) carried out the first systematic search for instabilities in anisotropic spherical models. He found that the polytropic models defined by equation (37) were stable to spherically symmetric modes, with the possible exception of the n = 1/2 model, which appeared to oscillate at a level slightly above the noise. (The n = 1/2 model is extreme in the sense that all stars have exactly the same energy.) Barnes, Goodman & Hut (1986) later established the stability of these models to non-spherical modes as well. Hénon went on to test the stability to radial perturbations of the "anisotropic polytropes" defined by

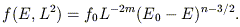
(38)

Models generated from equation (38) have velocity ellipsoids with fixed axis ratios _r² / _t² = (1 - m)^-1, where _r and _t are the 1D, radial and tangential components of the velocity dispersion tensor. Hénon found that the oscillatory instability that seemed to be present in the isotropic model with n = 1/2 became stronger as the velocity ellipsoid was made more prolate. He mapped out the region of instability in the (m, n)-plane and found that models with n as large as ~ 1 could be unstable when the velocity ellipsoid was sufficiently elongated.

Barnes, Goodman & Hut (1986) reanalyzed the stability of the anisotropic polytropes using a more sophisticated N-body code. They confirmed Hénon's results and noted that the instability boundary for radial modes could be approximated by n - m = 1/2, suggesting instability even for n = 3/2 when the orbits were fully radial. Barnes et al. noted that the stability boundary coincided roughly with the condition that the distribution of radial velocity have two peaks, and suggested that the "two-stream" nature of the velocity distribution was a necessary condition for this instability. They noted further that ðf / ðE > 0 was a requirement for a spherical model to have such a double-peaked distribution. Neither Hénon nor Barnes et al. discussed in detail the structure of their unstable models after they had reached a steady state, although the major effect of the instability seemed to be a radial spreading of stars.

The two conditions for instability established by these studies - ðf / ðE > 0, and radially-elongated velocity ellipsoids - imply an equilibrium density profile that diverges near the center, roughly as a power law. Until recently, such a density dependence was considered unphysical, but it is now known that early-type galaxies always have power-law density cusps ([Merritt & Fridman 1995]; [Gebhardt et al. 1996]). Further work on Hénon's instability would therefore be useful.

6.2. The radial-orbit instability

Antonov (1973) suggested that a spherical model constructed from purely radial orbits would be unstable to clumping of particles around any radius vector. ⁽⁷⁾ The instability was verified numerically by Polyachenko (1981), who followed the evolution of a 200-particle radial-orbit model into a bar. Barnes (1985) rediscovered the instability while using an N-body code to test the stability of Hénon's generalized polytropes; he observed growing barlike distortions in radially anisotropic models with a wide range of m's and n's.

The instability is similar to one first described by Lynden-Bell (1979) in the context of radially-hot disks. In spherical systems with well-behaved central potentials, elongated orbits are nearly closed, making slightly less than two radial oscillations for each circulation in angle. Such an orbit acts like a slowly precessing ellipse, or rod ([Polyachenko 1989]); the precession rate tends to zero for low L. In the presence of a barlike perturbation to the potential, an elongated orbit experiences a torque which causes it to precess more rapidly toward the bar; after passing through the bar, the orbit loses angular momentum and precesses more slowly. The result is an enhancement of the density in the neighborhood of the bar.

The strength of the instability, and its effect on the shapes of initially spherical models, were explored in a number of N-body studies. Merritt & Aguilar (1985) examined the stability of models with Dehnen's density law, = 2, and three different types of distribution function. They noted that the behavior of the instability depended sensitively on the low-L dependence of f. In models where the phase-space density was divergent at low L (as in Hénon's anisotropic polytropes), the growth rate of the instability and the final ellipticity of the model were found to be gradually increasing functions of the anisotropy. Even very mildly anisotropic models constructed from such distribution functions were found to be unstable. Barnes, Goodman & Hut (1986) reported similar behavior in their N-body study of Hénon's polytropes. Merritt & Aguilar also investigated a family of models generated from a distribution function of the form f = f (Q), Q = E + L² / 2r_a², in which the phase-space density is constant on spheroids in velocity space and everywhere finite. The latter models are characterized by a central region, r r_a, in which the motion is nearly isotropic and an outer envelope where the motion becomes increasingly radial ([Osipkov 1979]; [Merritt 1985]). Merritt & Aguilar found that the instability appeared suddenly in these models when r_a fell below a critical value, roughly 0.3 times the half-mass radius. The neutrally-stable model from this family had a global anisotropy ratio 2T_r / T_t 2.3, with T_r and T_t the kinetic energies in radial and tangential motions respectively.

Much of the subsequent work on the radial orbit instability has focussed on models with f = f (Q). Meza & Zamorano (1997) extended the Merritt & Aguilar study to include Dehnen models with a variety of cusp slopes . They found a mild dependence of the critical anisotropy ratio 2T_r/T_t on , from ~ 2.0 when = 2 (slightly less than the value found by Merritt & Aguilar for the same family) to ~ 2.6 for = 0. May & Binney (1986) used an adiabatic deformation technique to evaluate the stability of models with f = f (Q) and the isochrone density law. They estimated a critical value of ~ 2.2 for the anisotropy ratio. Dejonghe & Merritt (1988) found (2T_r / T_t)_crit 1.9 in f = f (Q) models with the Plummer density law. Bertin & Stiavelli (1989) used an N-body code to test the stability of models with distribution functions of the form f |E|^3/2 exp(aQ), designed to represent galaxies that form via radial collapse ([Stiavelli & Bertin 1985]; [Merritt, Tremaine & Johnstone 1989]). They found (2T_r / T_t)_crit 1.9. Stiavelli & Sparke (1991) derived a very similar criterion for instability in models with f |E|^3/2 exp(aE)/(1 + cL²). Perez et al. (1996) noted the presence of the instability in f = f (Q) models with the density profiles of isotropic polytropes. However they did not look closely at the critical parameter values defining the onset of the instability. Allen, Palmer & Papaloizou (1990) also noted the existence of the instability in an N-body study of modified polytropes but did not attempt to establish the stability boundary.

The existence of slowly-growing modes in models with very small global anisotropies, reported by Merritt & Aguilar (1985) and Barnes, Goodman & Hut (1986), calls into question the usefulness of diagnostics like 2T_r/T_t for judging instability. Palmer & Papaloizou (1987) showed that instability to barlike modes is in fact guaranteed in models where f is unbounded at small L, regardless of the degree of velocity anisotropy. These results prompted an analysis of the stability of a model of the giant elliptical galaxy M87 constructed by Newton & Binney (1984); their model is close to isotropic except near the center, where f increases rapidly at small L. The model was found to be mildly unstable to a barlike mode ([Merritt 1987b]).

An alternative to N-body techniques when evaluating the stability of equilibrium models is Kalnajs's (1972) matrix algorithm, which yields numerical expressions for the normal modes and their growth rates. Kalnajs's algorithm is in principle superior to N-body techniques when searching for the exact stability boundary in a family of models, but in practice the eigenvalue equation can be difficult to solve with accuracy when the growth rate is small. Polyachenko & Shukhman (1984) pioneered this approach in the study of spherical systems, deriving the lowest-order modes for a family of nearly-homogeneous models derived by Osipkov. They found instability for 2T_r / T_t 1.6. Results for two additional families - Hénon's generalized polytropes, equation (38), and a family of models based on Plummer's density law - were reported by Fridman & Polyachenko (1984). For the first family, a critical anisotropy ratio ~ 1.4 was quoted; however Palmer & Papaloizou (1987) proved that all radially-anisotropic models from this family would be unstable. For the second family, Fridman & Polyachenko found (2T_r / T_t)_crit 1.5; ⁽⁸⁾ Dejonghe & Merritt (1988), in an N-body study, found instability in this family for (2T_r / T_t)_crit 1.9.

Some of these inconsistencies can be attributed to the difficulties of implementing Kalnajs's technique. In a very convincing study, Saha (1991) derived the lowest-order unstable models for the family of anisotropic, f = f (Q) isochrone models first analyzed by May & Binney (1986). Saha found instability for 2T_r / T_t > 1.4, substantially smaller than May & Binney's estimate of 2.2; this result suggests that spherical models may be unstable over a much wider range of anisotropies than the N-body studies indicate. Saha (1992) went on to analyze a second family of isochrone models with a two-parameter distribution function; the first parameter r_a defined the size of the isotropic core, while the second parameter fixed the degree of anisotropy at large radii. Saha found a critical anisotropy ratio that ranged from 2T_r / T_t 2.3 in models whose envelopes contained purely radial orbits to ~ 1.8 in models where the asymptotic anisotropy was _r / _t 1.6. Weinberg (1991) derived the unstable modes for f = f (Q) models with the density profiles of isotropic Michie-King models; the latter constitute a one-parameter sequence characterized by the value of the dimensionless central potential W₀ (King 1966). Weinberg demonstrated instability for low r_a in models with several different values of W₀. For W₀ = 5, he found a critical anisotropy radius of r_a 1.2 in units of the King core radius. Bertin et al. (1994) evaluated the stability of the Stiavelli-Bertin (1985) models and found (2T_r / T_t)_crit 1.6, substantially less than in the earlier N-body study of Bertin & Stiavelli (1989).

These normal-mode calculations suggest that spherical models with 2T_r / T_t 2.3 are generally unstable, and that models with distribution functions that increase rapidly toward small L can be unstable for much lower values of the mean anisotropy. A model with 2T_r / T_t = 2.3 has an average ratio of radial to tangential velocity dispersions of _r / _t 1.5; thus, one might expect to never see more extreme anisotropies in spherical galaxies. One of the few galaxies for which the anisotropy has been convincingly measured is M87 ([van der Marel 1994]; [Merritt & Oh 1997]), where _r / _t 1.5 over a wide range in radius.

The radial-orbit instability would be expected to persist in axisymmetric models with radially-elongated velocity ellipsoids. Levison, Duncan & Smith (1990) reported barlike modes in highly flattened (c/a 0.4) oblate models when the radial velocity dispersion exceeded ~ 0.7 times the velocity disperision perpendicular to the meridional plane. This result suggests that the radial-orbity instability might be very effective in flattened models; it would be useful to verify the result in an independent study.

Elliptical galaxies often contain central mass concentrations which could strongly influence the elongated orbits that drive the radial-orbit instability. Palmer & Papaloizou (1988) discussed the effect of a central point mass on the instability of models with distribution functions peaked near L = 0. They noted that a central point mass greatly increases the precession rate of low-L orbits; at a given energy, there is a minimum precession rate corresponding to orbits with a certain nonzero L. If this minimum precession rate is larger, for most orbits, than the rate at which a barlike mode would grow in the model without a central point mass, they argued that the instability would be inhibited. Preliminary N-body simulations suggested a critical mass of the central object of roughly 0.1% the mass of the model, similar to the masses inferred for the nuclear black holes in a number of galaxies. Given the likely ubiquity of black holes in elliptical galaxies, more work along the lines of Palmer & Papaloizou's would be valuable.

Polyachenko (1981) noted that collapse from cold initial conditions tends to produce equilibrium systems with strong radial anistropies, and he pointed out that such systems would be unstable to nonspherical modes. He went on to verify ([Polyachenko 1985], 1992) the evolution of initially cold and spherical N-body clouds into bars. A number of subsequent studies have shown that a wide range of initial conditions can produce collapses where the radial-orbit instability is active. Merritt & Aguilar (1985) found that intially spherical clouds with an r^-1 density profile evolved into triaxial bars when (2T / |W|)₀ was less than about 0.2, with T and W the total kinetic and potential energies of the initial configuration. The final elongation was found to increase smoothly with decreasing initial "temperature"; the coldest initial conditions produced models with a final axis ratio of ~ 2.5 : 1. The instability was also found to reduce the central concentration of the relaxed models. Min & Choi (1989) also found a critical virial ratio of ~ 0.2 in collapses starting from homogeneous initial conditions. Aguilar & Merritt (1990) extended their earlier work to flattened and rotating initial conditions. They found that collapses with (2T / |W|)₀ 0.1 produced final shapes that were nearly uncorrelated with initial shapes; this characteristic final shape was approximately prolate with a 2 : 1 axis ratio. The minimum amount of rotation required to inhibit the bar instability was found to be 0.1, with the standard dimensionless spin parameter. Cannizzo & Hollister (1992) explored the dependence of the final shape of a collapsing cloud on its initial density profile. They distributed particles according to r^-n initially with 0 < n < 2.5 and set the virial ratio to a very low value, (2T / |W|)₀ 0.01. Their final configurations were approximately prolate, with axis ratios that varied from ~ 1.8 : 1 for n = 2.5 to ~ 1.3 : 1 for n = 0. ⁽⁹⁾ Theis & Spurzem (1998) carried out a series of direct-summation N-body collapse simulations using large numbers of particles (N 3 × 10⁴) and small softening lengths. Particles were initially distributed according to Plummer's law, with 2T / W 0.04. The final models were prolate/triaxial and very elongated, with c / a 0.4 - 0.5.

As a number of authors have noted, the final elongations of these models are close to the maximum value permitted by the bending instability discussed below. Polyachenko (1992) suggested that the distribution of elliptical galaxy axis ratios might be determined by the competition between these two instabilities. However recent determinations of the frequency function of elliptical galaxy intrinsic shapes ([Tremblay & Merritt 1995], 1996; [Ryden 1996]) find a peak near c / a 0.8, too round to be convincingly explained in this way.

6.3. Bending instabilities

Toomre (1966) showed that a thin stellar sheet has a tendency to buckle when the stars have large random velocities along the plane and are constrained to remain in a single thin layer as the sheet bends. ⁽¹⁰⁾ The constraining force comes from the vertical self-gravity of the sheet, which is large if the sheet is thin. Stars moving across a bend are forced to oscillate vertically as they pursue their unperturbed horizontal motions, and the bend will grow if the gravitational restoring forces from the perturbation are too weak to provide the vertical acceleration required. The thin-sheet dispersion relation is (Toomre 1966)

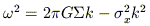
(39)

where _x is the velocity dispersion parallel to the sheet and is its surface density. The first term, which arises from the perturbed gravity, is stabilizing, while the second term, due to the centrifugal force that the stars exert on the sheet, is destabilizing. Because the stabilizing force decreases less rapidly with the wavelength of the bend than does the destabilizing force (^-1 vs. ^-2), short-wavelength perturbations are the most unstable. For sufficiently long wavelengths > _J = _x² / G, the gravitational restoring force dominates and the sheet is stable. Bending instabilities are precisely complementary, in this sense, to the Jeans instability in the plane, which is stabilized at wavelengths < _J. Toomre's analysis, which was based on the moment equations, was shown by Mark (1971) and Kulsrud, Mark & Caruso (1971) to be valid for slabs of arbitrary vertical structure whenever the wavelength of the perturbation greatly exceeds the thickness of the slab.

At wavelengths shorter than the actual vertical thickness of the layer, Toomre argued that the bending would once again be stabilized. Since the thickness of a slab scales as _z / G, with _z the vertical dispersion, Toomre noted that both long- and short-wavelength perturbations should be stabilized when _z / _x was sufficiently large. He estimated a critical value of 0.30 for this ratio. Polyachenko & Shukhman (1977) found a very similar value for the critical anisotropy in a homogenous slab, for which the bending takes the form of surface corrugations. Araki (1985) computed the exact linear normal modes of a finite-thickness slab with an anisotropic Gaussian velocity distribution. He found that bending at all wavelengths was stabilized when the ratio of vertical to horizontal velocity dispersions exceeded ~ 0.293, remarkably close to Toomre's earlier estimate. At the instability threshold, the single, neutrally-unstable mode has a wavelength of about 1.2 in units of _J.

The elongation of a pressure-supported galaxy with the Toomre-Araki critical anisotropy is approximately 1 : 15, which would seem to suggest that bending modes are unlikely to be important in structuring elliptical galaxies. But a number of subsequent studies revealed instability in much rounder models. Polyachenko & Shukhman (1979) and Vandervoort (1991) calculated the exact linear normal modes for constant-density stellar spheroids, both oblate and prolate. In models where the distribution function favored radial motions, both studies found critical axis ratios of ~ 1 : 3, not ~ 1 : 15. Merritt & Hernquist (1991) carried out an N-body study of inhomogeneous prolate models; they also found a critical axis ratio of 0.3 - 0.4.

Figure 13. Bending instability in a prolate, "shell-orbit" model (Merritt & Hernquist 1991). The initial model has axis ratio c/a = 0.1; frames are separated by ~ 4 periods of the long-axis orbit. The dominant mode is an antisymmetric bend that induces a long-lived peanut shape. Prolate models with elongations more extreme than ~ 3 : 1 are found to be unstable to bending modes.

The discrepancy was explained in the following way ([Merritt & Sellwood 1994]). In finite or inhomogenous models, the gravitational restoring force from the bend - represented by the first, stabilizing term in equation (39) - is substantially weaker than in infinite sheets and slabs. In fact, bending modes in thin systems with realistic density profiles are often not stabilized by gravity even at the longest wavelengths. However bending modes can still be stabilized in such systems, for the following reason. Stars in a finite-thickness system oscillate vertically with an unperturbed frequency _z; like any oscillator, the phase of a star's response to the imposed bending depends entirely on whether the forcing frequency kv_x is greater than or less than its natural frequency. If kv_x > _z for most stars, the overall density response to the perturbation will produce a potential opposite to that imposed by the bend and the disturbance will be damped. Merritt & Sellwood showed that this mechanism was responsible for the short-wavelength stabilization found by Toomre (1966) and Araki (1985) in the infinite slab. In a finite or inhomogeneous stellar spheroid, where the gravitational restoring force from the bend is much smaller than in an infinite slab, almost all of the stabilization is due to this out-of-phase damping. Since a typical star in such a system feels a vertical forcing frequency from a long-wavelength bend that is roughly twice the frequency _x of its orbital motion along the long axis, stability to global modes requires that the forcing frequency be less than _z, the frequency of orbital motion along the short axis. The resulting condition 2_x > _z predicts stability for a pressure-supported, homogeneous prolate spheroid rounder than ~ 1 : 2.94, in excellent agreement with the normal-mode calculations of and Fridman & Polyachenko (1984) and Vandervoort (1991).

Fridman & Polychenko (1984) went on to suggest that the absence of elliptical galaxies flatter than ~ E6 was due to bending instabilities. The work summarized above is consistent with their hypothesis, at least to the extent that elliptical galaxies are pressure-supported systems in which the stellar motions are largely radial. Merritt & Sellwood (1994) pointed out that oblate galaxies with azimuthally biased motions can remain stable even when somewhat flatter; indeed, Hunter & Toomre (1969) showed that even perfectly thin disks are stable to bending modes when all the stars orbit in one direction, since the bending wave is free to travel with the stars. Sellwood & Merritt (1994) followed the nonlinear evolution of oblate models with various initial velocity distributions and found that models where a modest fraction of the pressure was tangentially directed could reach equilibrium when still rather thin. They suggested that such models were reasonable representations of S0 galaxies like NGC 4550 that appear to contain two, nearly equal counter-rotating streams of stars ([Rubin, Graham & Kenney 1992]; [Merrifield & Kuijken 1994]).

Bending instabilities may also be relevant to the formation of galactic bulges. Rapidly-rotating disks are unstable to the formation of bars; early indications that these bars might thicken with time ([Combes & Sanders 1981]; [Combes et al. 1990]) were spectacularly confirmed by Raha et al. (1991) who carried out three-dimensional simulations revealing a violent buckling instability. Raha et al. argued that they were witnessing a coherent bending mode driven by the inequality between the stellar velocity dispersions along and perpendicular to the bar. The end result in their simulations was a thick, peanut-shaped sub-system very similar in appearance to the "boxy bulges" seen in some disk galaxies ([Shaw 1987]).

An alternative explanation for the thickening of N-body bars was proposed by Combes et al. (1990) and Pfenniger & Friedli (1991), who suggested that the bending was due to the vertical instability of the x₁, bar-supporting orbits. This instability first occurs at a 2 : 1 bifurcation, which generates a family of stable banana orbits perpendicular to the bar; as discussed above (Section 4.2.2), the vertical banana orbits appear to be heavily populated in 3D N-body bars. However the evidence is strongly against the hypothesis that the 2 : 1 bifurcation is responsible for the vertical thickening. The buckling of N-body bars is observed to be extremely coherent, particularly in initially thin bars, which bend almost into a V-shape (Raha et al. 1991). Friedli & Pfenniger (1990) found that the vertical thickening could be essentially eliminated by imposing reflection symmetry about the disk plane, which is the expected behavior for a collective mode but which has no natural explanation in terms of orbital instability. Merritt & Hernquist's (1991) observation of bending modes in integrable prolate models is also inconsistent with the Combes et al. hypothesis, since these models do not support banana orbits. The strong dependence of the bending rate on model thickness, seen in a number of studies, is also most naturally explained in terms of a collective instability. Merrifield (1996) noted that the condition 2_x < _z derived by Merritt & Sellwood (1994) for instability to large-scale bending modes also implies the existence of a 2 : 1 vertical resonance, a coincidence that may explain the early confusion about the origin of the bending.

6.4. Instabilities in radially-cold models

A disk constructed purely from circular orbits is locally Jeans-unstable and clumps into rings (Toomre 1964); this behavior is independent of the net rotation velocity, that is, the fraction of stars that rotate clockwise versus counterclockwise. These ringlike modes can be stabilized either by making the disk hot or by thickening the disk into a spheroid, for which the potential disturbance caused by a given perturbation in surface density is weaker than in a disk (Vandervoort 1970). Bishop (1988) reported the ring instability in a radially-cold oblate model with an axis ratio of 1 : 4. Merritt & Stiavelli (1990) found a critical axis ratio of ~ 0.4 for these unstable modes in the same family of thin-orbit models. De Zeeuw & Schwarzschild (1991) analyzed the same models yet a third time, using an adiabatic deformation technique, and estimated a critical axis ratio of ~ 0.33. The effect of radial pressure on the ring instability was addressed by Sellwood & Valluri (1997), who considered a family of two-integral oblate models. The radial pressure in a two-integral model increases with decreasing elongation, due to the equality of radial and vertical velocity dispersions; this implies a rapid stabilization of ringlike modes as the model is made rounder. Sellwood & Valluri found stability to axisymmetric modes at an axis ratio of ~ 1 : 4 in their models. Ringlike modes in axisymmetric models were also reported by Sellwood & Merritt (1994) and Robijn (1995).

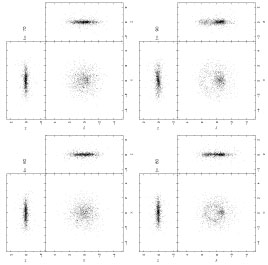
Figure 14. Lopsided instability in a nonrotating oblate model from the Kuzmin-Kutuzov (1962) family. The initial model has f = f (E, Lz2) and an axis ratio c/a 0.1; hence the stellar motions are nearly circular, with very little radial pressure. Modes like these persist in two-integral oblate models as round as c/a 0.2, and in even rounder models when the velocity ellipsoid is biassed toward circular motions.

The prevalence of m = 1 or lop-sided modes in slowly-rotating disks suggests that lop-sided modes would be the dominant ones in axisymmetric models whose rotation was too slow to encourage the formation of a bar. Nonrotating oblate models constructed from thin orbits (Section 3.2) are in fact unstable to lopsided modes regardless of their axis ratio ([Merritt & Stiavelli 1990]). Levison, Duncan & Smith (1990) reported lopsided modes in nonrotating, axisymmetric oblate models with axis ratio of ~ 0.4; the instability vanished when the radial velocity dispersion exceeded ~ 0.4 times the tangential velocity dispersion. Sellwood & Merritt (1994) also reported lopsided modes in their flattened, counter-rotating models and found that fairly large radial pressures were required for stability. In their study of two-integral oblate models, Sellwood & Valluri (1997) found instability to lopsided modes for c/a 0.2; in other words, the radial pressure of two-integral models rapidly stabilizes the modes as the models are made rounder. Sellwood & Valluri found that the lopsided modes became less important as the net rotation of their models was increased, but they persisted even in models with net angular momentum 90% that of a maximally rotating model. Robijn (1995) carried out a normal-mode analysis of Kuz'min-Kutuzov models with little radial pressure and confirmed the Merritt & Stiavelli result that such models were unstable to lopsided modes regardless of axis ratio. He found that the growth rate of lopsided modes was more strongly affected by increasing the radial velocity dispersion than by adding net rotation.

The persistence of unstable modes even in nearly spherical, radially-cold models suggests that precisely spherical galaxies composed of circular orbits might be unstable. Bisnovatyi-Kogan, Zel'dovich & Fridman (1968) showed that the circular-orbit sphere is always stable to radial modes, i.e. to clumping into spherical shells. However Fridman & Polyachenko (1984, Vol. 1, p. 179) showed that a circular-orbit sphere with a radially-increasing density, d / dr > 0, is generally unstable to non-spherically-symmetric modes. Barnes, Goodman & Hut (1986) explored such instabilities in their N-body study of Hénon's generalized polytropes. For m < 0, equation (38) implies a preponderance of nearly-circular orbits and a density profile that peaks at nonzero r. Barnes et al. found that all models with m - 1/2 exhibited quadrupole oscillations with growing amplitude, reaching stability only after a substantial rearrangement of matter.

6.5. The "tumbling bar instability"

Papaloizou, Palmer & Allen (1991) and Allen, Papaloizou & Palmer (1992) reported barlike instabilities in nearly spherical models with very small amounts of rotation. Additional arguments in favor of this "tumbling bar instability" were presented by Palmer (1994a, b). However, the instability appears not to exist. Sellwood & Valluri (1997) tested the stability of the Allen et al. models, using precisely the same files of initial particle coordinates but a different N-body code. No traces were found of growing modes, nor did Sellwood & Valluri find any unstable barlike distortions in another family of slowly-rotating, axisymmetric models. The evolution seen in the Allen et al. study was traced to an improper treatment of variable time steps in their N-body code.

6.6. Instabilities of triaxial models

The instabilities discussed above in spherical and axisymmetric models would be expected to persist in non-axisymmetric models with appropriate orbital populations. Smith & Miller (1982) were the first to search for dynamical instabilities in triaxial models, using an N-body code to evolve a realization of Schwarzschild'd (1979) model. Although they witnessed significant evolution in the shape of the model - the peanut-shaped isophotes of the initial configuration became much more nearly elliptical - Smith & Miller concluded that there was no evidence for exponentially-growing modes. De Zeeuw & Schwarzschild (1989) used an adiabatic deformation technique to look for unstable barlike modes in Statler's (1987) set of triaxial models based on the Perfect Ellipsoid. They confirmed the existence of a barlike instability for triaxial models in which box orbits were heavily populated. The instability appeared to vanish in triaxial models that were sufficiently elongated.

The preparation of this review was supported by NSF grants AST 93-18617 and AST 96-17088 and by NASA grant NAG 5-2803. I am very much indebted to W. Dehnen, P. Saha, J. Sellwood, M. Valluri and R. van der Marel who read substantial portions of the manuscript and made many suggestions for improvement. J. Perez and V. Polyachenko also made helpful comments. My understanding of the issues discussed here has benefitted enormously from discussions with A. Bahri, H. Kandrup, J. Binney, G. Contopoulos, O. Gerhard, J. Laskar, J. Meiss, A. Moser, Y. Papaphilippou, and Y. Sinai.

⁶ Distinguishing between the two sorts of instability in a numerical simulation can sometimes be difficult; see the discussion of bending instabilities in Section 6.3. Back.

⁷ Antonov's proof would seem to establish only the instability of the motion of a single particle and not necessarily the existence of a growing mode. Back.

⁸ In a reanalysis, Polyachenko (1985) found a critical ratio of slightly more than 2. Back.

⁹ Cannizzo & Hollister adopted a relatively large value for the interparticle softening length in their simulations, and this fact may explain the less extreme elongations found by them than by other authors who adopted similar initial conditions. Back.

¹⁰ Toomre has pointed out that the names "firehose" and "hose-pipe" are not really appropriate for this instability, which has more in common with the Kelvin-Helmholtz instability that occurs when two fluids slide past one another, or with beads sliding along an oscillating string (Parker 1958). Back.