


4.4. Synchronous gauge
Synchronous gauge, introduced by
Lifshitz (1946)
in his pioneering calculations of cosmological perturbation theory, is
defined by the conditions
 =
wi = 0, which eliminate two scalar fields
(
=
wi = 0, which eliminate two scalar fields
( and
the longitudinal part of w) and one transverse vector field
(w
and
the longitudinal part of w) and one transverse vector field
(w ).
It is not difficult to show that synchronous
coordinates can be found for any weakly-perturbed spacetime. However,
the synchronous gauge conditions do not eliminate all gauge freedom.
This has in the past led to considerable confusion (for discussion see
Press & Vishniac 1980
and Bardeen 1980).
).
It is not difficult to show that synchronous
coordinates can be found for any weakly-perturbed spacetime. However,
the synchronous gauge conditions do not eliminate all gauge freedom.
This has in the past led to considerable confusion (for discussion see
Press & Vishniac 1980
and Bardeen 1980).
Synchronous gauge has the property that there exists a set of comoving observers who fall freely without changing their spatial coordinates. (This is nontrivial when one notes that in order to remain at a fixed terrestrial latitude, longitude, and altitude above the surface of the earth it is necessary to accelerate everywhere except in geosynchronous orbits.) These observers are called "fundamental" comoving observers. The existence of fundamental observers follows from the geodesic equation
 |
(4.26) |
for the trajectory
xµ( ), where
d
), where
d = (-
ds2)1/2 for a timelike geodesic and
uµ = dxµ /
d
= (-
ds2)1/2 for a timelike geodesic and
uµ = dxµ /
d . With
. With
 =
wi = 0,
eq. (4.10) gives
=
wi = 0,
eq. (4.10) gives  00i = 0, implying that
ui = 0 is a geodesic.
00i = 0, implying that
ui = 0 is a geodesic.
Each fundamental observer carries a clock reading conformal
time  =
=
 dt /
a(t) and a fixed spatial coordinate label
xi.
The clocks and labels of the fundamental observers are taken to
define the coordinate values at all spacetime points (assuming that
these hypothetical observers densely fill space). The residual gauge
freedom in synchronous gauge arises from the freedom to adjust the initial
settings of the clocks and the initial coordinate labels of the
fundamental observers.
dt /
a(t) and a fixed spatial coordinate label
xi.
The clocks and labels of the fundamental observers are taken to
define the coordinate values at all spacetime points (assuming that
these hypothetical observers densely fill space). The residual gauge
freedom in synchronous gauge arises from the freedom to adjust the initial
settings of the clocks and the initial coordinate labels of the
fundamental observers.
Because the spatial coordinates xi of each fundamental
observer are held fixed with time, the xi in
synchronous gauge are Lagrangian
coordinates. This implies that the coordinate lines become highly deformed
when the density perturbations become large. When the trajectories of two
fundamental observers intersect the coordinates become singular: two
different sets of xµ label the same spacetime
event. This flaw of synchronous gauge is not apparent if
|
 /
/
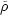 | << 1
and the initial coordinate labels are nearly unperturbed, so this gauge
may be used successfully (with some care required to avoid contamination
of physical variables by the residual gauge freedom) in linear perturbation
theory.
| << 1
and the initial coordinate labels are nearly unperturbed, so this gauge
may be used successfully (with some care required to avoid contamination
of physical variables by the residual gauge freedom) in linear perturbation
theory.
To be consistent with the conventional notation used for synchronous gauge
(Lifshitz 1946;
Lifshitz & Khalatnikov
1963;
Weinberg 1972;
Peebles 1993),
in this section only we shall absorb
 into
hij and double hij:
into
hij and double hij:
 |
(4.27) |
Using this line element and the definitions of the Ricci and Einstein tensors, it is straightforward (if rather tedious) to derive the components of the perturbed Einstein tensor:
 |
(4.28) |
 |
(4.29) |
 |
(4.30) |
One can easily verify that the unperturbed parts of the Einstein
equations G00 =
8 GT00 =
-8
GT00 =
-8 G
G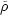 and
Gij =
8
and
Gij =
8 GTij =
8
GTij =
8 G
G
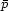
 ji
give the Friedmann and energy-conservation equations for the background
Robertson-Walker spacetime.
ji
give the Friedmann and energy-conservation equations for the background
Robertson-Walker spacetime.
Our next goal is to separate the perturbed Einstein equations into scalar, vector, and tensor parts. First we must decompose the metric perturbation field hij as in eqs. (4.13)-(4.15), with a term added (and the notation changed slightly) to account for the trace of hij:
 |
(4.31) |
where Dij was defined in eq. (4.15). We require
 i
hi =
i
hi =
 i
hiT = 0 to ensure that the last
two parts of hij are purely solenoidal (vector mode) and
transverse-traceless (tensor mode) contributions. The scalar mode variables
are h and
i
hiT = 0 to ensure that the last
two parts of hij are purely solenoidal (vector mode) and
transverse-traceless (tensor mode) contributions. The scalar mode variables
are h and
 -2
-2
 , whose Laplacian is
, whose Laplacian is
 . We shall not
worry about how to invert the Laplacian on a curved space but simply assume
that it can be done if necessary.
. We shall not
worry about how to invert the Laplacian on a curved space but simply assume
that it can be done if necessary.
The perturbed Einstein equations now separate into 7 different parts according to the spatial symmetry:
 |
(4.32) (4.33)
(4.36) (4.37) (4.38) |
The derivation of these equations is straightforward but tedious. They
have decomposed naturally into separate equations for the scalar, vector,
and tensor parts of the metric perturbation, with the sources for each
given by the appropriate part of the energy-momentum tensor. However,
there are more equations than unknowns! There are four scalar equations for
 and h,
two vector equations for hi, and one tensor equation
for hij,T. How can this be?
and h,
two vector equations for hi, and one tensor equation
for hij,T. How can this be?
Before answering this question, let us note another interesting feature of the equations above, which will provide a clue. The equations arising from G0µ involve only a single time derivative of the scalar and vector mode variables, while those arising from Giµ have two time derivatives, as we might have expected for equations of motion for the gravitational fields. This means that we could discard eqs. (4.32)-(4.34) and be left with exactly as many second-order in time equations as unknown fields. Alternatively, we could discard eqs. (4.35)-(4.37) and be left with exactly enough first-order in time equations for the scalar and vector modes. Only the tensor mode evolution is uniquely specified by a second-order wave equation.
The reason for this redundancy is that the twice-contracted Bianchi
identities of differential geometry,
 µ
Gµ
µ
Gµ = 0, force the Einstein eqs. (4.7) to imply
= 0, force the Einstein eqs. (4.7) to imply
 µ
Tµ
µ
Tµ = 0. The Einstein equations themselves contain
redundancy,
as we can check explicitly here. By combining the time derivative of eq.
(4.32) and the divergence of eqs. (4.33) and (4.34)
one obtains the perturbed part of eq. (4.24) (note, however,
that
= 0. The Einstein equations themselves contain
redundancy,
as we can check explicitly here. By combining the time derivative of eq.
(4.32) and the divergence of eqs. (4.33) and (4.34)
one obtains the perturbed part of eq. (4.24) (note, however,
that 
 -
h/6). Similarly, eq. (4.25) follows from the
time derivative of eqs. (4.33) and (4.34) combined with
the gradient of eqs. (4.35)-(4.37). Because we
require the equations of motion for the matter and radiation to locally
conserve the net energy-momentum, three of the perturbed Einstein eqs.
(4.32)-(4.38) are redundant.
-
h/6). Similarly, eq. (4.25) follows from the
time derivative of eqs. (4.33) and (4.34) combined with
the gradient of eqs. (4.35)-(4.37). Because we
require the equations of motion for the matter and radiation to locally
conserve the net energy-momentum, three of the perturbed Einstein eqs.
(4.32)-(4.38) are redundant.
In the literature, G00 =
8 GT00 is often called the
"ADM energy constraint" and G0i =
8
GT00 is often called the
"ADM energy constraint" and G0i =
8 GT0i is called
the "ADM momentum constraint" equation. The 3+1 space-time decomposition
of the Einstein equations into constraint and evolution equations was
developed in detail by Arnowitt, Deser & Misner
(1962,
ADM) and applied to cosmology by
Durrer & Straumann
(1988)
and Bardeen (1989).
The ADM
constraint equations may be regarded as providing initial-value constraints
on (h,
GT0i is called
the "ADM momentum constraint" equation. The 3+1 space-time decomposition
of the Einstein equations into constraint and evolution equations was
developed in detail by Arnowitt, Deser & Misner
(1962,
ADM) and applied to cosmology by
Durrer & Straumann
(1988)
and Bardeen (1989).
The ADM
constraint equations may be regarded as providing initial-value constraints
on (h,  ,
,
 ,
,
 ,
,
 i) and the
matter variables.
If these constraints are satisfied initially (this is required for a
consistent metric), and if eqs. (4.35)-(4.37) are
used to evolve (h,
i) and the
matter variables.
If these constraints are satisfied initially (this is required for a
consistent metric), and if eqs. (4.35)-(4.37) are
used to evolve (h,
 ,
,
 ,
,
 ,
,
 i) while the
matter
variables are evolved so as to locally conserve the net energy-momentum,
then the ADM constraints will be fulfilled at all later times. (This
follows from the results stated in the preceding paragraph.) In effect,
the Einstein equations have built into themselves the requirement
of energy-momentum conservation for the matter. If one were to integrate
eqs. (4.35)-(4.37) correctly but to violate
energy-momentum conservation, then eqs. (4.32)-(4.34)
would be violated.
i) while the
matter
variables are evolved so as to locally conserve the net energy-momentum,
then the ADM constraints will be fulfilled at all later times. (This
follows from the results stated in the preceding paragraph.) In effect,
the Einstein equations have built into themselves the requirement
of energy-momentum conservation for the matter. If one were to integrate
eqs. (4.35)-(4.37) correctly but to violate
energy-momentum conservation, then eqs. (4.32)-(4.34)
would be violated.
In practice, we may find it preferable to regard the ADM constraints alone - and not eqs. (4.35)-(4.37) - as giving the actual field equations for the scalar and vector metric perturbations. They have fewer time derivatives and hence are easier to integrate. Equations (4.35)-(4.37) are not necessary at all (although they may be useful for numerical checks) because they can always be obtained by differentiating eqs. (4.32)-(4.34) and using energy-momentum conservation.
This situation becomes clearer if we compare it with Newtonian gravity.
The field equation
 2
2
 =
4
=
4 Ga2
Ga2

 is analogous to
eq. (4.32). (We shall see this equivalence much more clearly
in the Poisson gauge below.) Let us take the time derivative:
is analogous to
eq. (4.32). (We shall see this equivalence much more clearly
in the Poisson gauge below.) Let us take the time derivative:
 2
2
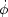 =
4
=
4 G
G
 (a2
(a2

 ). If we now
replace
). If we now
replace 
 (
(
 ) using the
continuity equation, we obtain a time evolution equation for
) using the
continuity equation, we obtain a time evolution equation for
 2
2
 analogous to
the divergence
of eq. (4.33). The solutions to this evolution equation obey
the Poisson equation if and only if the initial
analogous to
the divergence
of eq. (4.33). The solutions to this evolution equation obey
the Poisson equation if and only if the initial
 obeys the Poisson
equation. Why should one bother to integrate
obeys the Poisson
equation. Why should one bother to integrate
 2
2
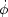 in time
when the solution can always be obtained instantaneously from the Poisson
equation? Viewed in this way, we would say that the extra time derivatives
in the
Giµ equations have nothing to do with
gravity per se.
The real field equations for the scalar and vector modes come from
the ADM constraint equations.
in time
when the solution can always be obtained instantaneously from the Poisson
equation? Viewed in this way, we would say that the extra time derivatives
in the
Giµ equations have nothing to do with
gravity per se.
The real field equations for the scalar and vector modes come from
the ADM constraint equations.
If the scalar and vector metric perturbations evolve according to
first-order in time equations, their solutions are not manifestly
causal (e.g., retarded solutions of the wave equation). We shall
discuss this point in detail in section 4.7.
However, for now
we may note that the tensor mode obeys the wave eq. (4.38).
The solutions are the well-known gravity waves which, as we shall
see, play a key role in enforcing causality. The source for these waves
is given by the transverse-traceless stress (generated, for example,
by two masses orbiting around each other). The


 term arises because we use comoving coordinates and the K term arises
as a correction to the Laplacian in a curved space; otherwise the vacuum
solutions are clearly waves propagating at the speed of light.
Abbott & Harari (1986)
show that eq. (4.38) is the Klein-Gordon
equation for a massless spin-two particle.
term arises because we use comoving coordinates and the K term arises
as a correction to the Laplacian in a curved space; otherwise the vacuum
solutions are clearly waves propagating at the speed of light.
Abbott & Harari (1986)
show that eq. (4.38) is the Klein-Gordon
equation for a massless spin-two particle.