6. Comparison with the Observations

As noted earlier, there are some 20 broad, isolated emission lines, and a similar number of narrow lines, that can be measured and compared with the model calculations. Each observed line ratio conveys different information about the line emission region, and there are more than enough constrains on the models. At this stage we are only interested in integrated line intensities. Later we discuss the information obtained from line variability (chapter 8) and line profiles (chapter 9).

6.1 The Broad Line Region

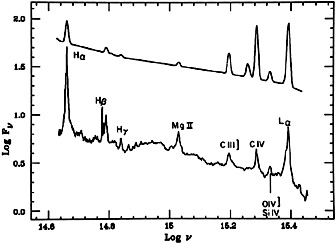
Fig. 14 shows a comparison of the composite quasar spectrum of Fig. 2 and the theoretical model of Fig. 11. The calculated line intensities, up to r_out = 2 × 10¹⁸ cm, are put on top of an artificial continuum, similar in shape to the observed one, and normalized to give the observed L equivalent width.

Figure 14. A comparison of a composite quasar spectrum (bottom) with model calculations.

6.1.1 Resonance metal lines. The strong ultraviolet lines of CIV1549, NV1240 and OVI1035 are good indicators of the gas temperature and ionization parameter. As seen from Table 1 and Fig. 14, the calculated strength of these lines, relative to L, are in fairly good agreement with the observations. The agreement is not as good in models of smaller U, although, a harder ionizing continuum can compensate, somewhat, for that. It has been proposed that optically thin BLR clouds, combined with much smaller ionization parameters, can explain the strong high excitation lines. Such clouds are expected to have very strong NV1240, OVI1035 and HeII lines. Their contribution to the total broad line flux is large only if their covering factor is much greater than the covering factor of the optically thick clouds.

The CIII]1909 / CIV1549 line ratio has been used, in the past, to deduce the ionization parameter. The models presented here clearly show this line ratio to be insensitive to the exact value of U. In fact, the line ratio is in good agreement with the observations over most of the range calculated, and disagreement appears only where the contribution of lower density material starts to dominate the spectrum.

6.1.2 Intercombination lines. Semi-forbidden lines such as CIII]1909, NIII]1750, OIII]1663 and NIV]1486, are weak in the inner part of the BLR, where the density is above their critical density ( 10^9.5 cm^-3 for CIII]1909). Further out, where the density is lower, such lines can be important coolants, and the energy distribution among the different cooling agents is changed. The presence of strong intercombination lines is a sign that the contribution of N_e > 10¹⁰ cm^-3 material to the emitted spectrum is not significant.

6.1.3 Broad forbidden lines. With the N r^-s, s > 0 density law considered here, some forbidden lines, such as [OIII]4363, are predicted to be strong in large r clouds, where the density drops to their critical density ( 10⁸ cm^-3). Strong, broad forbidden lines are never observed, although there are hints to the presence of weak, broad [OIII]5007 in some objects. Thus, there seems to be a natural limit to the extent of the BLR. This may be due to the radial dependence of the covering factor at large r, to clouds becoming optically thin, or to some other reasons.

6.1.4 The hydrogen spectrum. The calculated intensity of L in the s = 2 model (Fig. 11) increases with r much like the predicted r^5/6 dependence of (62). This reflects, mostly, the increase in the covering factor, and suggests that a fixed proportion of all ionizing photons are converted to L. It resembles the so called "recombination Case B flux", occurring in lower density nebulae, where each absorbed Lyman continuum photon results in the emission of a L photon. In AGN BLR clouds, the situation is more complicated, due to the high density and large optical depth. However, in many models the calculated L flux is within a factor 2 of the simple, "Case B" value.

Despite the simple atomic configuration, the good atomic data and the big improvements in the treatment of line transfer, the hydrogen line spectrum of AGNs is not yet well understood. This is demonstrated in Fig. 14 where it is evident that the calculated H and H lines are much weaker, relative to L, than in the observations. This has come to be known as the "L / H" problem. It is not yet clear whether it reflects wrong physical assumptions, the inaccuracy of the calculations or, perhaps, some reddening.

Regarding wrong physical assumptions, there are two proposed explanations. The first invokes a very strong, hard X-ray continuum, extending to MeV energies, and the second, extreme column densities ( 10²⁵ cm^-2). The two are not without difficulties. A strong X-ray--ray continuum is observed only in very few AGNs (there are only very few such observations) while the "L / H" problem seems to be common to most objects. There are also problems in violating the -ray background if all AGNs have such a hard continuum. Large column densities are appealing for some reasons (see below) but the large Compton depth makes the line transfer calculations questionable, and there are difficulties associated with the physical size of the clouds in low luminosity objects (chapter 8).

The most likely cause for inaccurate calculations is the simplified escape probability treatment. Typical BLR clouds are expected to have huge L and H optical depths ((L) ~ 10⁸, (H) ~ 10⁴), and the local nature of this transfer method may not be adequate for such extreme conditions. Among the present dustless models, that use as an input the typical observed continuum, some get close to explaining the observed L / H ratio and some manage to reproduce the observed Balmer decrement, but none is successful in explaining both.

Line reddening is another possible explanation which is not without its difficulties. It is discussed in chapter 7.

6.1.5 The helium spectrum. The optical depth in many HeI lines must be large because of the high population of the HeI 2³S metastable level. The HeI5876, HeI10830 and other HeI line intensities are likely to be affected by that, and accurate transfer calculations are required.

To date most accurate calculations consider an up to 100 level HeI atom, with optical depth in all lines. Such a large number of levels is needed since three-body recombination is important in populating the high energy HeI levels at the BLR densities. The calculated line intensities are quite reliable, but not reliable enough to use the model helium/hydrogen line ratios to determine the helium abundance.

The calculations of the HeII spectrum are much simpler. The optical depth in all lines, except for the Lyman series and, perhaps, HeII1640, is small, and the three-body recombination process is not as important as in hydrogen. A notable problem is the HeII304 L line, which is a major ionization source for hydrogen and a major fluorescence excitation source for OIII. The approximate methods (chapter 4) that are used leave much to be desired and the calculated line intensity is rather uncertain. The observation of this line is a major challenge of space astronomy and a real comparison with the calculations is still to come. Another complication is the wavelength coincidence between the hydrogen L and the HeII H lines (separation of 0.498Å). This is a potential pumping source for the HeII n = 4 level but it is thought to be unimportant because of the small optical depth in the HeII H line, and the relatively large wavelength difference, The result of the small optical depth, and the good atomic data, is that the HeII1640 / 4686 line ratio is easy to calculate. This line ratio is an important reddening indicator and its use in determining the reddening in AGN clouds is explained in chapter 7.

6.1.6 FeII and MgII lines. The low excitation lines of FeII and MgII are produced in the partly neutral region of the BLR clouds. Such regions are thought to be heated and ionized by X-ray photons. They are characterized by T_e 10⁴K and N_H⁰ / N_H⁺ 10.

While MgII2798 is a relatively simple line to calculate, this is not the case for the FeII lines, because of the extremely complicated energy level configuration of Fe⁺. There are several thousand FeII transitions to be considered, many with a large optical depth. The atomic data for this ion is poorly known and reliable cross sections are only starting to become available. An additional complication is the large number of wavelength coincidences of different FeII lines; more than 300 (!) with separation less than 10 km s^-1. This is a major population process for the levels that must be taken into account. Other potentially important processes are the absorption of incident continuum radiation in FeII lines and the continuos opacity due the hydrogen n = 2 level.

The large number of FeII lines form several distinct emission bands at 2200-2600Å, 3000-3400Å, 4500-4600Å and 5250-5350Å. The strongest ultraviolet FeII lines originate from some odd parity levels with energies of ~ 5 eV above the ground. Other ultraviolet lines, out of energy levels as high as 9 eV, are also observed. Such lines are not consistent with collisional excitation at the deduced electron temperature of ~ 10⁴K and fluorescence or some other unknown processes must be responsible for that. All this is not unique to AGNs. The same FeII lines are known to be strong in the spectrum of symbiotic stars; galactic objects with no hard X-ray continuum.

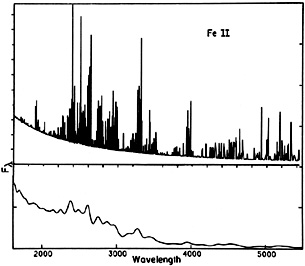
Fig. 15 demonstrates the complicated nature of the FeII spectrum. It shows a calculated FeII spectrum, for AGN clouds, with more than 3000 FeII lines. There is no way to isolate most of these lines, because of their large number and the broad line profiles. The convolution of the theoretical spectrum with a typical observed line profile (bottom part of the diagram) form broad, shallow emission features that demonstrate the difficulties in measuring the continuum luminosity, and the intensity of lines such as MgII2798 and H, in spectral regions rich in FeII lines. The conglomerations of the strong FeII lines, the Balmer continuum, and other spectral features, creates a noticeable energy excess between the wavelengths of 2000 and 4000Å. This feature is sometimes referred to as the "small bump" and was confused, in the past, with the underlying nonstellar continuum of AGNs.

Figure 15. Top: A theoretical FeII spectrum on top of a power-law continuum. Bottom: the same spectrum but lines are 4000 km s-1 gaussians.

6.1.7 CaII lines. These are the lowest ionization lines observed in the spectrum of AGNs. The strongest feature is the infrared triplet at 8498, 8542 and 8662Å. The lines are observed in about 1/3 of all objects, while other CaII lines, such as the H, K and the forbidden lines near 7300Å, are weak or absent. Theoretical modeling shows that the internal CaII line ratios, and their strength relative to H, requires very large column densities, N_col ~ 10²⁵ cm^-2. Such models are appealing for some theoretical reasons (energy budget, to be explained below, the L / H problem) but there are difficulties as well. For example, objects with very weak CaII infrared lines are not very different, spectroscopically, from objects with strong CaII lines. In particular, strong CaII emitters are not very different in their L / H from weak CaII emitters. If large column densities are essential to explain both the observed L / H and CaII lines in AGNs, it is not very clear why the CaII lines are not more common. Furthermore, very large column density clouds, with typical BLR densities, are more than 10¹⁵ cm thick, a dimension which is of the order of the cloud-central source separation in low luminosity AGNs (chapter 8).

6.1.8 Diffuse continua. The free-free continuum and several of the bound-free continua (Paschen, Balmer) are cavations.

6.1.9 Very high excitation metal lines. These lines (CIII977, OIII835 etc.) are calculated to be strong at small r high density clouds, where the temperature is high due to the collisional suppression of other cooling agents, such as CIV1549. The lines are weak or unobserved in most AGN spectra which is another argument against having a large contribution from very high density clouds to the broad-line spectrum.

6.1.10 Small dense BLR. Some gas clouds may survive in the innermost part of the BLR, where the radiation field is most intense. These must have very high densities (~ 10¹² cm^-3) since low density material will not achieve thermal equilibrium at this environment (chapter 9). The clouds may be associated with the inflow of gas from the BLR, or perhaps produced near the central black hole. At such high densities the gas must be close to thermal equilibrium, most cooling is via bound-free and free-free emission and no line emission is likely to be important. The clouds are therefore reprocessing the central continuum radiation, absorbing it at some frequencies and re-emitting in others. The resulting spectrum can resemble, in some ways, the spectrum of a thin accretion disk, showing a "blue bump" in optical and ultraviolet energies and a strong edge at the Lyman limit. Currently there are too few observational constraints, and too many theoretical uncertainties, to put this idea into a serious observational test.