


The discussion in the previous chapters gave support to the accepted model of AGN emission line regions. Such regions are thought to contain numerous optically thick clouds, that are exposed to the intense ionizing flux of a central source. The origin, stability and motion of these clouds, and the resulting line profiles, are the subjects of this chapter.
9.1.1 Important time scales: Several time scales must be considered in relation to the formation, stability and motion of the clouds.
The recombination time: This is the time required to reach ionization equilibrium. It is given by
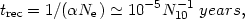
| (76) |
where N10 is the density in units of 1010 cm-3.
The dynamical time: This is the crossing time (or orbital time) of the line emitting region. For the BLR
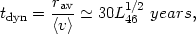
| (77) |
where the previous relation between the average dimension and the luminosity (75) has been used.
The sound crossing time: This is the time required to establish pressure equilibrium within a single cloud. The total cloud thickness is not well determined but the thickness of the ionized gas is estimated to be 1012-13 cm for the BLR clouds. This gives
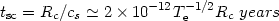
| (78) |
where Rc is the cloud radius in cm and cs = sqrt[ 2kTe / mp] is the sound speed.
9.1.2 Confinement. The mass of individual BLR clouds, as deduced from the models, is well below their Jeans mass, i.e. self gravity is negligible. In the absence of confinement, such clouds will disintegrate on a time scale of tsc. Since this time is much shorter than the dynamical time, the clouds must be confined or else be continuously produced throughout the BLR, which requires extremely large mass flux through the line emission region.
One way to confine the clouds is by a Hot Intercloud Medium (HIM), much like in the interstellar medium. Such a "two-phase model" has been the subject of extensive investigations. Magnetic confinement is another possibility that needs to be considered. Below is a short description of the hot intercloud medium model.
9.1.3 The two-phase model. In this model the
cool (Te
 104K)
gas is in pressure
equilibrium with a lower density, much hotter gas, of temperature
THIM, filling
the volume between the clouds. Heating and cooling of the hot gas is
mainly by
Compton and inverse Compton scattering, and THIM is
given by the Compton temperature
104K)
gas is in pressure
equilibrium with a lower density, much hotter gas, of temperature
THIM, filling
the volume between the clouds. Heating and cooling of the hot gas is
mainly by
Compton and inverse Compton scattering, and THIM is
given by the Compton temperature
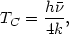
| (79) |
where h is the
mean photon energy, weighted by the cross section. In this
limit the temperature is independent of the gas density and is
determined only
by the energy distribution of the incident continuum. As a result,
THIM is the same throughout the line emitting region.
is the
mean photon energy, weighted by the cross section. In this
limit the temperature is independent of the gas density and is
determined only
by the energy distribution of the incident continuum. As a result,
THIM is the same throughout the line emitting region.
The special feature of the two-phase model is that a single parameter
controls the ionization and thermal properties of both components. The
parameter, called  is
defined by
is
defined by
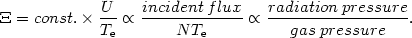
| (80) |
The value of this parameter is the same for the hot and cool gas at a certain location. 6
The  vs. Te dependence is the key to the understanding of
the two-phase
model. At small
vs. Te dependence is the key to the understanding of
the two-phase
model. At small  the
temperature is kept around 104 K due to bound-free and
collisional excitation cooling. At this value of
the
temperature is kept around 104 K due to bound-free and
collisional excitation cooling. At this value of
 there is only one
solution to the kinetic temperature. At much larger
there is only one
solution to the kinetic temperature. At much larger
 , the ionization
increases, the cooling is
less efficient, and no equilibrium can be achieved until Compton cooling
become dominant, at about 107 - 108 K. In some
cases there is a small range in
, the ionization
increases, the cooling is
less efficient, and no equilibrium can be achieved until Compton cooling
become dominant, at about 107 - 108 K. In some
cases there is a small range in
 where
the thermal equilibrium conditions may allow both Comptonized gas
and low
temperature gas to coexist and there is a two temperature solution for the
same pressure. This is demonstrated in
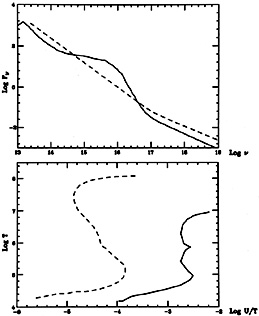
Fig. 22 that shows the calculated
Te vs. U / Te curve for two
different continua, one with a two phase solution and one without.
where
the thermal equilibrium conditions may allow both Comptonized gas
and low
temperature gas to coexist and there is a two temperature solution for the
same pressure. This is demonstrated in
Fig. 22 that shows the calculated
Te vs. U / Te curve for two
different continua, one with a two phase solution and one without.
|
Figure 22. Calculated Te vs. U/Te (bottom) for the two incident continua shown in the upper panel. The solid line is the "standard" continuum (Fig.7) adopted in this work. The dashed line is a two-component power-law continuum, with spectral indices of 1.2 in the infrared-ultraviolet and 0.7 in the X-ray. A two-phase solution (S shaped part of the curve) can only be obtained for the power-law continuum (courtesy of T. Kallman) |
A two-phase equilibrium can only exist at high enough
THIM, where the T
vs. U/T curve is S shaped. In this case there are two
stable branches, at low (~
104 K) and high (~ 108 K)
temperatures, allowing thermal instabilities to grow
and develop into a two-component atmosphere. Only one of the continua shown
in the diagram (in dashed line) gives this kind of curve. Older
photoionization
models assumed this continuum to be typical of AGNs. It was consistent with
THIM  108K and a two-phase model for the gas. Moreover,
estimates of the
ionization parameter, obtained from emission line ratios, agreed roughly
with
the U/T required for the two-phase instability. Since this is the
only range
in which hot and cold gas can coexist, it suggests a specific value of
U for the
BLR clouds. This was considered to be the explanation for the fact that the
ionization parameter in faint Seyferts and bright quasars, a factor of a
thousand in luminosity apart, is roughly the same.
108K and a two-phase model for the gas. Moreover,
estimates of the
ionization parameter, obtained from emission line ratios, agreed roughly
with
the U/T required for the two-phase instability. Since this is the
only range
in which hot and cold gas can coexist, it suggests a specific value of
U for the
BLR clouds. This was considered to be the explanation for the fact that the
ionization parameter in faint Seyferts and bright quasars, a factor of a
thousand in luminosity apart, is roughly the same.
Unfortunately, more realistic continua, like the one used throughout this work, changed this result. This continuum has a large ultraviolet excess which results in more Compton cooling. The highest temperature is around 107 K, too low to allow a two-phase solution (solid line in Fig. 22). (7) Thus the idea of a stable two-phase BLR, in the form presented here, is questionable. Today it is also known that the allowed range in U is in fact quite large (chapters 4 - 6) and the motivation for a specific value of U is not as strong.
A hot inter-cloud medium with THIM ~ 107
K presents some other problems.
First, the optical depth to electron scattering may be large. We can
estimate this from the pressure equilibrium condition and the
pressure-radius dependence
of chapter 5, P
 r-s, with s ~ 2:
r-s, with s ~ 2:
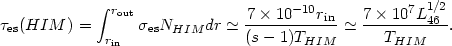
| (81) |
In making this estimate we have assumed that rout >> rin, the BLR density at rin is 1011 cm-3, the temperature of the cold clouds is 104 K, and the luminosity-size relation is as in equation (75). This shows that luminous objects, with low THIM, are opaque to electron scattering. This would have observable consequences. Large amplitude continuum variations will be smeared out and broad electron scattering wings will appear in all emission lines. Moreover, the K-shell opacity in iron and other elements can exceed the electron scattering opacity, and will show up as strong absorption X-ray edges. Such effects are not observed.
There are serious dynamical implications to a cool stationary HIM. Typical velocities in the BLR are several thousands kms-1, much larger than the sound speed in a cool HIM. A super-sonic motion through this medium must result in drag forces, Rayleigh-Taylor instability and breakup of the clouds. This leads to fragmentation into optically thin filaments, in contradiction with the observed strong lines of MgII and FeII. There are additional difficulties and more reasons to abandon the idea of a stable, two-phase model.
The HIM, if it exists, need not be stable. There are additional heating mechanisms, (superthermal particles, radio frequency heating) and the pressure equilibrium may not be exact since cloud evaporation will tend to raise the cloud pressure over the HIM pressure. Line radiation pressure is known to be important in the cold clouds and can exceed the cold gas pressure in cases of a large ionization parameter. A simple pressure equilibrium may not be achieved if this is the dominant pressure inside the clouds. A relativistic intercloud medium can help to solve some of the difficulties, especially the cloud instability problem, since in this case the drag force is very small.
Finally, we should comment on the probable scaling laws for the pressure
and density for a stable, or unstable hot confining medium. Using the
notation
of chapter 5, the value of s is likely
to be in the range of 3/2 to 5/2, i.e. the
assumption of P  r-2 is quite adequate for such cases.
r-2 is quite adequate for such cases.
9.1.4 Magnetic confinement. This is a new
idea that has received little attention
so far. The field strength required to confine the BLR clouds is about 1
G and its possible origin may be in a relativistic wind, an accretion
flow or an accretion
driven wind. Magnetically-confined clouds would have a filamentary structure
and would tend to elongate along the field lines. The pressure laws expected
are P  r-5/2 in an accretion flow and P
r-5/2 in an accretion flow and P
 r-2 in a relativistic wind.
r-2 in a relativistic wind.
6
 is referred, in some
papers, as "the ionization parameter". This should not be confused
with U, as defined here, which has no temperature dependence.
Back.
is referred, in some
papers, as "the ionization parameter". This should not be confused
with U, as defined here, which has no temperature dependence.
Back.
7 This temperature may be angle dependent, if the ultraviolet source is a thin accretion disk continuum (chapter 10). Back.