


2.5. Morphological classification of clusters
A number of different cluster properties have been used to construct morphological classification systems for clusters. Somewhat surprisingly, these different systems are highly correlated, and it appears that clusters can be represented very crudely as a one-dimensional sequence, running from regular to irregular clusters (Abell, 1965; 1975). There is considerable evidence that the regular clusters are dynamically more evolved and relaxed than the irregular clusters. The various morphological classification schemes are described below, and the way in which they fit into the one-dimensional sequence is summarized in Table 1, which is adapted from Abell (1975) and Bahcall (1977a).
| Property | Regular | Intermediate | Irregular |
| Zwicky Type | Compact | Medium-Compact | Open |
| Bautz-Morgan Type | I,I-II,II | II,II-III | II-III,III |
| Rood-Sastry Type | cD,B,L,C | L,C,F | F,I |
| Galactic Content | Elliptical-rich | Spiral-poor | Spiral-rich |
| E:S0:Sp | 3:4:2 | 1:4:2 | 1:2:3 |
| Morgan Type | ii | i-ii | i |
| Oemler Type | cD,Spiral-poor | Spiral-poor | Spiral-rich |
| Symmetry | Spherical | Intermediate | Irregular |
| Central Concentration | High | Moderate | Low |
| Subclustering | Absent | Moderate | Significant |
| Richness | Rich | Rich-Moderate | Rich-Poor |
n*
 102 102
| n*
 101 101
| n*
 100 100
| |
Zwicky et al. (1961-1968) classified clusters as compact, medium compact, or open. A compact cluster has a single pronounced concentration of galaxies, with more than ten galaxies appearing in contact as seen on the plate. A medium compact cluster has either a single concentration with ten galaxies separated by roughly their own diameters, or several concentrations. An open cluster lacks any pronounced concentration of galaxies.
Bautz and Morgan (1970) give a classification system based on the degree to which the cluster is dominated by its brightest galaxies. Bautz-Morgan Type I clusters are dominated by a single, central cD galaxy; cD galaxies have the most luminous and extensive optical emission found in galaxies (see Section 2.10.1). In Type II clusters, the brightest galaxies are intermediate between cD and normal giant ellipticals, while in Type III, there are no dominating cluster galaxies. Type I - II and Type II- III are intermediates. Leir and van den Bergh (1977) have classified 1889 rich Abell clusters on the Bautz-Morgan system, and some of the newer southern catalogs (e.g., White and Quintana, 1985) give Bautz-Morgan types for their clusters.
The original Rood-Sastry (1971) classification system is based on the nature and distribution of the ten brightest cluster galaxies. Basically, the six Rood-Sastry (RS) classes are defined as follows:
Rood and Sastry (1971) give classifications for low redshift Abell clusters on this system. They show that these classifications form a bifurcated sequence, which can be represented by a 'tuning-fork' diagram (Figure 3a). This sequence is correlated with the sequence of regular to irregular clusters in the sense that clusters on the left of the diagram (cD and B) are regular and those to the right (F and I) are irregular. Rich clusters are more or less equally distributed among the three arms of the diagram.
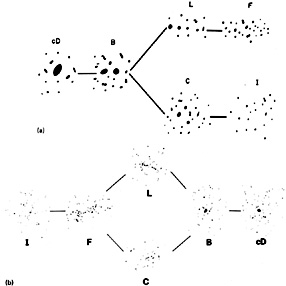
|
Figure 3. (a) The Rood-Sastry (1971) cluster classification scheme. (b) The revised Rood-Sastry classes from Struble and Rood (1982). |
Recently, Struble and Rood (1982, 1985) have proposed a revised version of the RS classification system. The definitions have been revised slightly, and a number of subclasses of the main RS classes have been proposed. More significantly, Struble and Rood have rearranged the tuning fork diagram into a 'split linear' diagram (Figure 3b), based on systematic trends in the galaxy distribution and content of clusters. This new scheme was devised in part from a comparison to numerical N-body simulations of the collapse of clusters (White, 1976c; Carnevali et al., 1981; Farouki et al., 1983; also see Figure 5). Struble and Rood propose that this sequence represents an evolutionary sequence of clusters from irregular I to cD clusters.
Morgan (1961) and Oemler (1974) have constructed classification systems based on the galactic content of clusters (that is, the fraction of cluster galaxies which are spirals (Sps), disk galaxies without spiral structure (S0s), or elliptical (Es)). Morgan (1961) classified clusters as type i if they contained large numbers of spirals and as type ii if they contained few spirals. Oemler (1974) has refined this system, defining three classes of clusters: spiral-rich clusters, in which spirals (Sp) are the most common galaxies; spiral-poor clusters, in which spirals are less common and S0s are the most common galaxies; and cD clusters, which are dominated by a central cD galaxy and in which the great majority of galaxies are ellipticals or S0s.
These systems of classification are empirically found to be highly correlated, and can roughly be mapped into a one-dimensional sequence running from regular clusters to irregular clusters (Abell 1965, 1975). As shown in Table 1, regular clusters are highly symmetric in shape, and have a core with a high concentration of galaxies toward the center. Subclustering is weak or absent in regular clusters. In contrast, irregular clusters have little symmetry or central concentration, and often show significant subclustering. This suggests that the regular clusters are, in some sense, dynamically relaxed systems, while the irregular clusters are dynamically less-evolved and have preserved roughly their distribution of formation. Additional evidence that regular clusters are dynamically relaxed is provided in Sections 2.6, 2.7, and 2.10.1, and the nature of the dynamical processes that might produce this relaxation is discussed in Section 2.9.
Regular clusters tend to be compact (Zwicky type), Bautz-Morgan Type I to II, Rood-Sastry types cD or B, Morgan type ii, Oemler spiral- poor or cD clusters. These last four correlations indicate a connection between the dynamical state and galactic content of clusters. There is no one-to-one correlation between the morphology of a cluster and its richness; regular clusters are always rich, while irregular clusters may be either rich or sparse. However, regular clusters tend to have higher central galaxy densities than irregular clusters, because they are at least as rich and more compact.