2.10. Galactic content of clusters

In the discussion of the morphological classification of clusters (Section 2.5), it was noted that the regular, compact clusters have a galactic content that differs markedly from that of the field. First, these clusters are often dominated by a single very luminous (cD) galaxy, or by a pair of very bright galaxies. Second, elliptical and S0 galaxies predominate over spiral galaxies in regular, compact clusters, where the opposite is true in the field. In this section possible origins for these differences are described and are related to the overall picture of cluster evolution given in the preceding section.

2.10.1. cD galaxies

cD galaxies were defined by Mathews, Morgan, and Schmidt (1964) as galaxies with a nucleus of a very luminous elliptical galaxy embedded in an extended amorphous halo of low surface brightness. They are usually found at the center of regular, compact clusters of galaxies (Morgan and Lesh, 1965; Bautz and Morgan, 1970), and about 20% of all rich clusters contain cD galaxies. However, some galaxies that appear to be cDs have been found in poor clusters and groups (Morgan, Kayser, and White, 1975; Albert, White, and Morgan, 1977).

cD galaxies are extremely luminous; if one excludes nuclear sources (Seyfert galaxies, N galaxies, and quasars), they are, as a class, the most luminous galaxies known. Sandage (1976) and Hoessel (1980) find average absolute magnitudes <M_V>_cD -23.7 + 5 log h₅₀ and -22.7 + 5 log h₅₀ for apertures of 43/h₅₀ kpc and 19/h₅₀ kpc, respectively. Since the galaxies extend well beyond this, total luminosities are at least a magnitude brighter. Moreover, the magnitudes of cDs show a rather small dispersion ( 0.3 mag) and are only weakly dependent on cluster richness (Sandage, 1976). cD galaxies are usually considerably brighter (often by a full magnitude) than other galaxies in the same cluster.

The question naturally arises as to whether cD galaxy luminosities simply represent the high end of the normal galaxy luminosity function, or whether cDs are 'special'. The distribution of brightest galaxy luminosities L₁ in a cluster would be p(L₁)dL₁ = exp(-N(L₁))dN(L₁) if the brightest galaxies were drawn at random from the integrated luminosity function N(L) (Section 2.4). This distribution would produce a large dispersion in L₁ and a strong dependence on cluster richness (neither of which are observed), unless the luminosity function were much steeper than is observed at the bright end (Sandage, 1976). However, cD luminosities themselves are too high to be drawn from the galaxy luminosity function (Schechter, 1976), unless it were less steep than is observed. While selection effects may account for the small dispersion of brightest elliptical and S0 galaxies in groups and clusters (Schechter and Peebles, 1976), it does not appear that this can explain the high luminosities of cD galaxies. A number of statistical tests (Sandage, 1976; Tremaine and Richstone, 1977; Dressler, 1978a) indicate that the magnitudes of cD galaxies cannot be drawn statistically from a general galaxy luminosity function.

cD galaxies are more extended than the other giant elliptical galaxies in two ways (see Figure 6a and 6b where the surface brightness of the cD in A1413 is compared to the giant elliptical NGC1278 in the Perseus cluster). First, the core regions of cDs are apparently larger. Hoessel (1980) finds that cD galaxies have core radii that average <r_c(gal)> 4 / h₅₀ kpc, while typical giant elliptical galaxies have <r_c(gal)> 0.4 / h₅₀ kpc (here, the surface brightness of the galaxy at projected radius b assumed to vary as {1 + [b/r_c(gal)]²}^-1). Unfortunately, these core radii represent fairly small angles and their determination may be ambiguous (Dressler, 1984). If one fits galaxy surface brightnesses to a de Vaucouleurs (1948a) form (equation 2.14), the effective radii r_e of cD galaxies are roughly a factor of two larger than the effective radii of normal giant elliptical galaxies. Alternatively, one can define the integrated luminosity slope

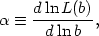
(2.37)

where L(b) is the luminosity observed within the projected radius b. Hoessel (1980) finds <>_cD 0.59 for b = 19 / h₅₀ kpc, which is about twice the value found for typical giant ellipticals.

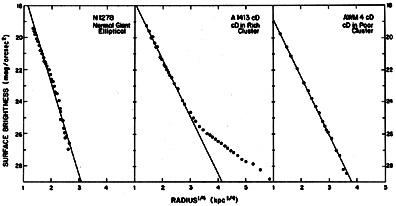
In cD galaxies in rich clusters, the giant elliptical-like core of the galaxy is embedded in a very extended low surface brightness halo (Oemler, 1973, 1976; Carter, 1977; Dressler, 1979). In Figures 6a,b the surface brightness of the very extended cD in the cluster A1413 is compared to that of a typical giant elliptical galaxy NGC1278 in the Perseus cluster (Oemler, 1976). The solid line shows a de Vaucouleurs fit (equation 2.14) to each galaxy. This profile fits the inner parts of either galaxy reasonably well, but the cD in A1413 has a halo of low surface brightness extending to beyond 1 Mpc from the galactic center. The surface brightness in cD haloes generally falls off as roughly the 3/2 power of projected distance from the galaxy center.

Figure 6. The surface photometry of cD galaxies. The surface brightness in magnitudes per square second of arc is plotted against the one-fourth power of the radius. The dots are the observed points, and the straight lines are de Vaucouleurs fits to the inner points. NGC1278 (Oemler, 1976) is a normal giant elliptical galaxy, showing no extended halo. The middle figure shows the cD in the cluster A1413 (Oemler, 1976), with a more extended central de Vaucouleurs profile and a very extended halo. The right panel is the cD in the poor cluster AWM4 (Thuan and Romanishin, 1981), which has an even more extensive de Vaucouleurs profile, but no apparent halo.

Masses of cD galaxies have been estimated by a measurement of the stellar velocity dispersion in the outer parts of the cD in A2029 (Dressler, 1979) and by measurements of the velocities of smaller companion galaxies which are assumed to be bound to the cD (Wolf and Bahcall, 1972; Jenner, 1974). Typically, one finds M 10¹³ M, but it is difficult to separate the galaxy and cluster mass distributions in the outermost parts of the cD (Dressler, 1979). For the same central velocity dispersion, cD galaxies are about 60% brighter than other giant ellipticals (Malumuth and Kirshner, 1981).

cD galaxies are usually found very near the centers of compact clusters (Morgan and Lesh, 1965; Leir and van den Bergh, 1977; White, 1978a). They also have velocities very near the mean velocity of galaxies in the cluster (Quintana and Lawrie, 1982), and may in fact give a better estimate of the cluster mean velocity than the average value for a few bright galaxies. These results suggest that cDs are usually sitting at rest at the bottom of the cluster gravitational potential well.

cD galaxies often have double or multiple nuclei (Minkowski, 1961; Morgan and Lesh, 1965; Hoessel, 1980; Schneider and Gunn, 1982); that is, there are several peaks in the surface brightness within the central part of the cD. Many cDs appear to be in binary or multiple galaxy systems (Leir and van den Bergh, 1977; Rood and Leir, 1979; Struble and Rood, 1981); when two cD nuclei appear to be surrounded by a common halo, these are referred to as 'dumbbell' galaxies. One important problem with these multiple nuclei is whether they are physically associated with and bound to the cD, or whether they are chance projections. In many cases, the multiple nuclei have rather large velocities relative to the cD, and cannot be bound to it (Jenner, 1974; Tonry, 1984, 1985a, b; Hoessel et al., 1985). These multiple nuclei must then be chance projections. Such projections would be unlikely if galaxies in clusters have isotropic velocity dispersions and constant surface number density cores. However, they are much more likely if galaxies have radial orbits, and the cluster density has a cusp near the center (Tonry, 1985a; Merritt, 1984b, 1985), as appears to be the case in many clusters (Beers and Tonry, 1986; Section 2.7).

The special structural and kinematic properties of cD galaxies suggest that they have been formed or modified by dynamical processes in clusters. Gallagher and Ostriker (1972) and Richstone (1975, 1976) have suggested that cDs consist of the debris from galaxy collisions. In a rich cluster, the outer envelopes of galaxies will be stripped by tidal effects during these collisions. The rate of mass loss due to tidal collisions in a cluster was derived by Richstone (1976); if his rate is integrated over a Schechter luminosity function (Section 2.4) and an isothermal galaxy density function with core radius r_c (Section 2.7), one finds

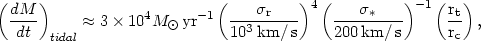
(2.38)

where _r is the cluster line-of-sight velocity dispersion (Section 2.6), and r_t and _gal are the tidal (outermost) radius and line-of-sight stellar velocity dispersion of a typical galaxy (L = L^*; see Section 2.4). Equation (2.38) assumes that all the cluster mass is in galaxies; if this is not the case, then the rate of mass loss from galaxies is reduced by the square of the fraction of mass in galaxies.

Knobloch (1978a, b) and Da Costa and Knobloch (1979) have argued that Richstone's expression overestimates the rate of mass loss, because the tidal stripping of a galaxy halo is limited by the rate of diffusion of stars into the halo. However, they take as their basic model a galaxy in which the halo mass is very small; this does not agree with the determinations of the mass distributions in galaxies (see, for example, Faber and Gallagher, 1979). For realistic mass models, it appears that the claimed discrepancy is a factor of roughly (_* / _r).

If most of the mass in a cluster were initially in extended (r_t r_c 300 kpc) haloes of dark material bound to individual galaxies, equation (2.38) shows that these dark haloes could have been stripped by tidal interactions within the age of a cluster, as was suggested in Section 2.8.

The outer portions of the luminous material would also be stripped (Strom and Strom, 1978a, 1979); if we assume a tidal radius of r_t 0.1r_c 30 kpc, we would expect 10¹² L of luminous material to be stripped from galaxies in a compact cluster. The stripped material would settle to the center of the cluster gravitational potential; because of the dependence of the collision rate on the square of galaxy density, the stripped material would probably be somewhat more centrally condensed than the galaxy distribution in the cluster. This tidal debris might thus be observed as the extended halo about a central cD galaxy. The stripped material would be centered on the cluster center, be at rest (on average) relative to the cluster center-of-mass, and have a mass and spatial distribution similar to that observed for cD haloes. This model for the formation of cD haloes (Gallagher and Ostriker, 1972; Richstone, 1975, 1976) predicts that they have high velocity dispersions, as has been observed for the cD in A2029 by Dressler (1979). This tidal debris model may explain the observed properties of cD haloes; however, it cannot naturally explain the giant elliptical galaxy nucleus of the cD.

Ostriker and Tremaine (1975), Gunn and Tinsley (1976), and White (1976a, 1977a) have suggested that cD galaxies are produced by the merger of massive galaxies within the core of a cluster. As discussed in Section 2.9, dynamical friction causes the orbits of massive cluster galaxies to decay. As such galaxies reach the cluster center, they merge to form a single supergiant galaxy, which swallows any galaxies that subsequently pass through the cluster center. The merger hypothesis (called 'galactic cannibalism' by Ostriker and Hausman, 1977) provides an attractive explanation for the formation of cD galaxies in a cluster.

First of all, since a cD galaxy would be produced by the merger of many of the more luminous galaxies in a cluster, the high luminosities of cDs (in excess of that expected from the galaxy luminosity function) is naturally explained. Once a massive galaxy reachs the cluster center, it will swallow other galaxies. Initially, its luminosity will increase at the rate (Ostriker and Tremaine, 1975)

(2.39)

where r_t is the tidal radius of the central galaxy, r_c and _r are the core radius and velocity dispersion of the cluster, and M/L_V is the visual mass-to-light ratio of all galaxies in the cluster. (Very recently, Merritt (1985) has shown that equation 2.39 greatly overestimates the actual merger rate at early times in a cluster.) Once most of the massive galaxies within the core have been accreted, the luminosity grows as t^1/2 rather than as t (Ostriker and Tremaine, 1975):

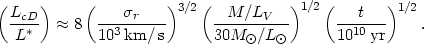
(2.40)

Thus luminosities of L_cD 10L^* can be produced during the lifetime of a compact cluster.

The merger product should be larger than the initial galaxy, because the kinetic energy of the merging galaxies 'heats' and inflates the final product (Ostriker and Hausman, 1977; Hausman and Ostriker, 1978). Hausman and Ostriker (1978) argue that the galaxy core radius r_c(gal) will increase by roughly a factor of ten, and the structure parameter by a factor of at least two, in rough agreement with the observations (Hoessel, 1980).

With the large increase in the luminosity of the first-brightest galaxy through mergers (equation 2.40), it might seem surprising that these galaxies show a rather small dispersion in absolute magnitude (Sandage, 1976). The observed magnitudes are for fixed measuring apertures, which are generally much smaller than the halo size of the cD; depending on the amount of swelling the cD undergoes, the observed magnitude may either increase or decrease (Gunn and Tinsley, 1976). In the simulations of Hausman and Ostriker (1978), the apparent magnitude within an aperture of 16 kpc remains roughly constant once the massive galaxies in the core of the cluster have been swallowed. This may explain the small dispersion in observed cD absolute magnitudes.

The first-brightest galaxy grows in luminosity by swallowing other massive galaxies; this increases the contrast between the first-brightest and the other bright galaxies (Gunn and Tinsley, 1976; Hausman and Ostriker, 1978), as is observed (Sandage, 1976; Tremaine and Richstone, 1977; Dressler, 1978a; McGlynn and Ostriker, 1980).

Of course, the process of dynamical friction and merging leaves the merger product nearly at rest relative to the average cluster galaxy and nearly at the center of the cluster, as is observed for cDs.

If a cluster is elongated, then the merger product at its center will tend to be elongated in the same direction. In general, cD galaxies are more highly flattened than other ellipticals (Leir and van den Bergh, 1977; Dressler, 1978c), and the axes of the cDs align with those of their clusters, as predicted (Sastry, 1968; Rood and Sastry, 1972; Dressler, 1978c, 1981; Carter and Metcalfe, 1980; Binggeli, 1982).

If cD galaxies are produced by mergers of massive galaxies, one expects mergers to take place roughly every 10⁹ years (Ostriker and Hausman, 1977). The actual merger will occur over roughly an orbital period in the cD galaxy 3 × 10⁸ years (White, 1978b), and for this period the nucleus of the merging galaxy will be visible within the cD envelope. Thus one would expect about 1/4 of cD galaxies to have multiple nuclei, roughly as is observed (Hoessel, 1980). However, a major problem with this interpretation of multiple nuclei in cDs is that these nuclei, in many cases, have rather large velocities relative to the cD (Jenner, 1974; Tonry, 1984, 1985). This suggests that they are not bound to the cD, but might only be cluster galaxies seen in projection against the cD.

Rood and Leir (1979) find that about 1/4 of all cD galaxies are binaries (actually dumbbells); they argue that this fraction is much larger than is expected due to dynamical friction and merging. The reason is that in these systems the two galaxies in the binary differ by less than a magnitude in apparent luminosity. However, the primary component of the system would have swallowed roughly five other galaxies in the merger picture, and therefore should be much brighter than its companion. Since one magnitude corresponds to a factor of 2.5 in brightness, and magnitudes at a fixed aperture do not increase directly with total luminosity because of swelling, it is not clear how serious a discrepancy this is (see also Tremaine, 1981).

The dynamical friction and merger theory may explain most of the observed properties of cD galaxies except for their very extended haloes. The tidal debris theory explains the extended haloes, but not the properties of the inner elliptical galaxy. It seems natural to suggest that cD galaxies result from the action of both types of processes.

However, Merritt (1983, 1984a, b, 1985) has recently pointed out some very serious problems with this simple picture of cD formation. He argues that the tidal effect of the global cluster potential (as opposed to that due to individual galaxy interactions) dominates the evolution of cluster galaxies. Tidal stripping of galaxies would then lower their masses and prevent any mergers. If this argument is correct and if mergers formed cDs, then the mergers must have occurred before the cluster collapsed, perhaps in smaller subclusters or groups (Carnevali et al., 1981; van den Bergh, 1983a, Dressler, 1984).

Theories of the origin of cD galaxies can be tested through observations of the apparent cD galaxies in 23 poor clusters which were discovered by Morgan, Kayser, and White (1975) (hereafter MKW) and Albert, White, and Morgan (1977) (hereafter AWM). These clusters range in Abell richness (Section 2.3) from < 10 to 50 galaxies; none are richer than Abell richness class zero (Bahcall, 1980). These clusters have velocity dispersions _r (Stauffer and Spinrad, 1978) and core radii r_c (Bahcall, 1980) which are probably about 1/2 of those of rich, compact clusters. Since the dynamical friction rate (when summed over all galaxies) varies as _r / r_c (equation 2.30) and the merger rate varies as _r / r_c⁴ (equation 2.39), one expects mergers to form remnants in these poor clusters even larger than those in rich clusters. On the other hand, the tidal stripping rate (equation 2.38) varies as _r⁴ / r_c, and is thus much lower in poor clusters. If mergers form the extended elliptical galaxy body of a cD and tidal debris makes up the very extended halo, the cDs in poor clusters should lack such haloes. Surface photometry of the cDs in poor clusters (Oemler, 1976; Stauffer and Spinrad, 1980; Thuan and Romanishin, 1981) indicates that this is indeed the case. In Figure 6c, the surface photometry of the cD in the poor cluster AWM4 as observed by Thuan and Romanishin (1981) is shown.

While the processes of merging and tidal stripping, perhaps in preexisting subclusters and groups, seem to provide a possible explanation of many of the unusual properties of cD galaxies, the core of a rich compact cluster is a very active physical environment in which many other processes may be important. For example, recent X-ray and optical observations suggest that central, dominant galaxies are accreting vast quantities of gas, as much as 400 M / yr in the case of NGC1275 in the Perseus cluster (Sections 4.3.3 and 5.7). The accreting galaxies include a number of cDs. There are several arguments which suggest that the accreted gas is being converted into low mass stars (Cowie and Binney, 1977; Fabian et al., 1982a; Sarazin and O'Connell, 1983); if so, accretion can significantly increase the core luminosities of cDs (Fabian et al., 1982a; Sarazin and O'Connell, 1983).

Finally, I would like to comment on a semantic issue that has arisen concerning cDs and other similar galaxies. It should be clear from the discussion above that cDs represent the extreme result of a number of dynamical processes which must be occurring continuously in clusters and groups. There are a number of related types of galaxies which share many but not all of the properties of cDs; they may be extended, and be the brightest galaxy in a cluster (or nearly so), and be located at the spatial and velocity center of the cluster. In Section 4.4.2 we shall see that such galaxies may affect the X-ray morphology of clusters, even if they do not satisfy the technical definition of a cD galaxy; examples are M87 in the Virgo cluster and NGC1275 in the Perseus cluster. It has sometimes been argued that the definition of cD galaxies should be extended in some way to include all such objects. It seems to me that this is not a good idea; it is more useful to retain the degree of specificity in the original definition of cD galaxies, based on their optical properties as defined by Morgan and his collaborators (Mathews, Morgan, and Schmidt, 1964). I suggest that a new term, 'central dominant galaxy' (abbreviated cd?) be used for galaxies that are the brightest cluster member or within 0.5 magnitudes of the brightest, and that appear to be at rest at the cluster center.