5.4. Transport processes

Processes that redistribute energy, momentum, or heavy elements within the intracluster gas will now be reviewed.

5.4.1 Mean free paths and equilibration time scales

The mean free paths of electrons and ions in a plasma without a magnetic field are determined by Coulomb collisions. As in the stellar dynamical case, it is important to include distant as well as nearby collisions. The mean free path _e for an electron to suffer an energy exchanging collision with another electron is given by (Spitzer, 1956)

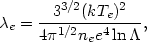
(5.32)

where T_e is the electron temperature, n_e is the electron number density, and is the ratio of largest to smallest impact parameters for the collisions. For T_e 4 × 10⁵ K, this Coulomb logarithm is

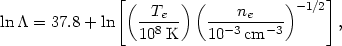
(5.33)

which is nearly independent of density or temperature. Equation (5.32) assumes that the electrons have a Maxwellian velocity distribution at the electron temperature. The equivalent mean free path of ions _i is given by the same formula, replacing the electron temperature and density with the ion temperature T_i and density, dividing by the ion charge to the fourth power, and slightly increasing ln . In the discussion that follows the ions will generally be assumed to be protons, and the diffusion of heavy elements will be discussed in Section 5.4.5 below. Numerically,

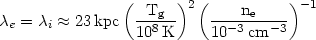
(5.34)

assuming that T_e = T_i = T_g.

In general, these mean free paths are shorter than the length scales of interest in clusters ( 1 Mpc), and the intracluster medium can be treated as a collisional fluid, satisfying the hydrodynamic equations. Note that the mean free paths are comparable to the size of a galaxy, however, and in the interaction between intracluster gas and individual galaxies the gas may be nearly collisionless, as mentioned previously (Section 5.3.4).

If a homogeneous plasma is created in a state in which the particle distribution is non-Maxwellian, elastic collisions will cause it to relax to a Maxwellian distribution on a time scale determined by the mean free paths (Spitzer, 1956, 1978). Electrons will achieve this equilibration (isotropic Maxwellian velocity distribution characterized by the electron temperature) on a time scale set roughly by t_eq(e, e) _e / <v_e>_rms, where the denominator is the rms electron velocity,

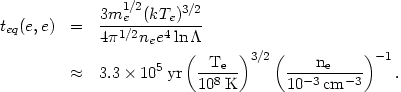
(5.35)

The time scale for protons to equilibrate among themselves is t_eq(p, p) (m_p / m_e)^1/2 t_eq(e, e), or roughly 43 times longer than the value in equation (5.35). Following this time, the protons and ions would each have Maxwellian distributions, but generally at different temperatures. The time scale for the electrons and ions to reach equipartition T_e = T_i is t_eq(p, e) (m_p / m_e)t_eq(e, e), or roughly 1870 times the value in equation (5.35). For heavier ions, the time scales for equilibration are generally at least this short if the ions are nearly fully stripped, because the increased charge more than makes up for the increased mass. For T_g 10⁸ K and n_e 10^-3 cm^-3, the longest equilibration time scale is only t_eq(p, e) 6 × 10⁸ yr. Since this is shorter than the age of the cluster or the cooling time, the intracluster plasma can generally be characterized by a single kinetic temperature T_g. Under some circumstances, plasma instabilities may bring about a more rapid equilibration than collisions (McKee and Cowie, 1977).