4.4. Implementation of a Quadrupole Flow

In the discussion of VELMOD in Section 2, it was assumed that the IRAS-predicted velocity field, for the correct value of _I, is as good a model as can be obtained. However, there can be additional contributions to the local flow field from structures beyond the volume surveyed (R 12,800 km s^-1), as well as from shot noise-induced and Wiener filter-induced differences between the true and derived density fields beyond 3000 km s^-1 but within the IRAS volume (cf. Appendix B).

Fortunately, the nature of this contribution is such that we can straightforwardly model its general form and thus treat it as a quasi-free parameter (see below) in the VELMOD fit. Let us write the error in the IRAS-predicted velocity field due to incompletely sampled fluctuations as v_err(r). Because the total peculiar velocity field, v + v_err, must satisfy equation (4), and because v does so by construction (eq. [3]), it follows that v_err must have zero divergence. Moreover, if we suppose that v_err corresponds to the growing mode of the linear peculiar velocity field, it must have zero curl well. These properties will be satisfied if v_err is given by the gradient of a velocity potential that satisfies Laplace's equation. Such a potential may be expanded in a multipole series, each term of which vanishes at the origin (where, by construction, v_err must itself vanish).

The leading term in the resulting expansion of v_err is a monopole, v_err⁽⁰⁾(r) = Ar, or Hubble flow-like term. However, such a term is degenerate with the zero point of the TF relation (Section 3.3) and thus is undetectable. The next term in the expansion is a dipole, v_err⁽¹⁾ = B, or bulk flow independent of position. Like the monopole term, however, the dipole term is undetectable, because we work in the frame of the Local Group. Whatever bulk flow is generated by distant density fluctuations is shared by the Local Group as well. The leading term in the expansion of v_err(r) to which our method is sensitive is therefore a quadrupole term. Such a term represents the tidal field of mass density fluctuations not traced by the IRAS galaxies. We may write the quadrupole velocity component as

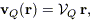
(19)

where _Q is a 3 × 3 matrix. In order for both the divergence and the curl of v_Q(r) to vanish, _Q must be a traceless, symmetric matrix. Consequently, it has only five independent elements, two diagonal and three off-diagonal.

We could allow for the presence of such a quadrupole in VELMOD by treating these five elements as free parameters. However, this is a dangerous procedure, because the modeled quadrupole would then have the freedom to fit the quadrupole already present in the IRAS velocity field, which is generated by observed density fluctuations. We wish to allow for the external quadrupole, but we do not want it to fit the -dependent quadrupolar component of the IRAS-predicted velocity field. In other words, we want the external quadrupole to be that required for the true value of _I, which we do not know a priori, rather than the "best-fit" value at any given _I. This problem would indeed be very serious if inclusion of the quadrupole made a large difference in the derived value of _I. Fortunately, however, it does not. As we show below, we obtain a maximum likelihood value _I = 0.56 when the quadrupole is not modeled. When we treat all five components of the quadrupole as free parameters for each _I, we obtain _I = 0.47. ⁽¹²⁾ Because the best-fit quadrupole is relatively insensitive to _I, we can estimate the external quadrupole by averaging the fitted values of the five independent components obtained for _I = 0.1, 0.2, ..., 1.0. In this way, we "project out" the _I-independent part of the quadrupole. In our final VELMOD run, we use this average external quadrupole at each value of _I. Throughout, we ignore the very small effect that this quadrupole might have on the derived IRAS density field.

In Figure 4, this quadrupole field is plotted on the sky in Galactic coordinates for a distance of 2000 km s^-1. The inflow due to the quadrupole, which occurs near the Galactic poles, is of greater amplitude than the outflow, which occurs at low Galactic latitude. The quadrupole reaches its maximum amplitude at l 165°, b 55°, in the direction of the Ursa Major cluster, as well as on the opposite side of the sky. In Section 5, when we plot VELMOD residuals on the sky with and without the quadrupole, the need for the quadrupole field shown in Figure 4 will become clear. Indeed, we will show in Section 5 that the VELMOD fit is statistically acceptable only when the quadrupole is included. Table 2 tabulates the numerical values of the independent elements of _Q that generate this flow. The rms value of this quadrupole over the sky is 3.3%, pleasingly close to the value we expect from theoretical considerations (Appendix B).

Figure 4. The external quadrupolar velocity field used in the VELMOD analysis, plotted in Galactic coordinates. The open symbols indicate negative radial velocities, and the stars indicate positive radial velocities. The amplitude of the quadrupole is shown for a distance r = 2000 km s-1. As indicated by eq. (19), the quadrupole flow increases linearly with distance at a given position on the sky. The maximum amplitude of the quadrupole at this distance is 147 km s-1, which occurs at l 165°, b 55°, as well as on the opposite side of the sky.

TABLE 2
NUMERICAL RESULTS FROM VELMOD ANALYSIS OF REAL DATA

Quantity	Value	Comments
Q(x, x)	37 km s-1	At 2000 km s-1 (cf. eq. [19])
Q(y, y)	36 km s-1	At 2000 km s-1 (cf. eq. [19])
Q(x, y)	15 km s-1	At 2000 km s-1 (cf. eq. [19])
Q(x, z)	113 km s-1	At 2000 km s-1 (cf. eq. [19])
Q(y, z)	-24 km s-1	At 2000 km s-1 (cf. eq. [19])
v	125 km s-1
wLG,x	-30 km s-1
wLG,y	-10 km s-1
wLG,z	30 km s-1
bA82	10.36 ± 0.36	10.29 ± 0.22 (Mark III value)
AA82	-5.96 ± 0.09	- 5.95 ± 0.04 (Mark III value)
TF,A82	0.464 ± 0.026	0.47 ± 0.03 (Mark III value)
bMAT	7.12 ± 0.22	6.80 ± 0.08 (Mark III value)
AMAT	-5.75 ± 0.09	- 5.79 ± 0.03 (Mark III value)
TF,MAT	0.453 ± 0.013	0.43 ± 0.02 (Mark III value)
I	0.492 ± 0.068	With quadrupole
I	0.563 ± 0.074	Without quadrupole
I	0.489 ± 0.084	A82 data only
I	0.498 ± 0.107	MAT data only
I	0.453 ± 0.093	0 < czLG 1350 km s-1
I	0.495 ± 0.133	1350 < czLG 2150 km s-1
I	0.573 ± 0.142	2150 < czLG 3000 km s-1
I	0.521 ± 0.050	wLG = 0; v fixed to 250 km s-1
I	0.491 ± 0.045	wLG = 0; v fixed to 150 km s-1
I	0.544 ± 0.071	With quadrupole; 500 km s-1 smoothing
I	0.635 ± 0.083	Without quadrupole; 500 km s-1 smoothing
I	0.510 ± 0.038	With quadrupole; TF parameters fixed at Mark III values
I	0.517 ± 0.039	Without quadrupole; TF parameters fixed at Mark III values
We did not do a likelihood search in parameter space to find formal error bars on quantities other than I. Error estimates for the TF parameters come from averaging over the mock catalog VELMOD runs (see Table 1).

When both the quadrupole and the Local Group random velocity vector are modeled, the radial peculiar velocity u(r) that enters into the likelihood analysis (see eq. [9]) is given by

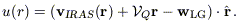
(20)

We emphasize again that while the three components of the Local Group random velocity w_LG are treated as free parameters in VELMOD, the five independent parameters of _Q are not, with the exception of a single run that we used to obtain and then average their fitted values at each _I. In the final run, from which we derive the estimate of _I quoted in the abstract, the quadrupole velocity field shown in Figure 4 was used at each value of _I.

¹² This value differs from the value of 0.49 quoted in the abstract because ultimately we will not allow the components of the quadrupole to be free parameters at each value of _I. Back.