A. Internal vs. External Shocks

1. General Considerations

Consider a "quasi" spherical relativistic emitting shell with a radius R, a width and a Lorentz factor . This can be a whole spherical shell or a spherical like section of a jet whose opening angle is larger than ^-1. Because of relativistic beaming an observer would observe radiation only from a region of angular size ~ ^-1. Consider now photons emitted at different points along the shock (see Fig. 18). Photons emitted by matter moving directly towards the observer (point A in Fig. 18) will arrive first. Photons emitted by matter moving at an angle ^-1 (point D in Fig. 18) would arrive after t_ang = R / 2c ². This is also, t_R, the time of arrival of photons emitted by matter moving directly towards the observer but emitted at 2R (point C in Fig. 18). Thus, t_R t_ang [94, 370]. This coincidence is the first part of the argument that rules out external shocks in variable GRBs.

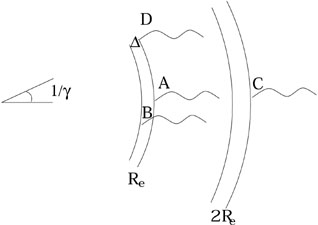Figure 18. Different time scale from a relativistic expanding shell in terms of the arrival times (ti) of various photons: tang = tD - tA, tR = tC - tA and t = tB - tA.

At a given point particles are continuously accelerated and emit radiation as long as the shell with a width is crossing this point. The photons emitted at the front of this shell will reach the observer a time t = / c before those emitted from the rear (point B in Fig. 18). In fact photons are emitted slightly longer as it takes some time for the accelerated electrons to cool. However, for most reasonable parameters the cooling time is much shorter from the other time scales [367] and I ignore it hereafter.

The emission from different angular points smoothes the signal on a time scale t_ang. If t t_ang t_R the resulting burst will be smooth with a width t_ang t_R. The second part of this argument follows from the hydrodynamics of external shocks. I show later in Section VIC (see also Sari and Piran [370]) that for external shocks / c R / c ² t_R t_ang and for a spreading shell R / c ². Therefore external shocks can produce only smooth bursts!

As we find only two time scales and as the emission is smoothed over a time scale t_ang, a necessary condition for the production of a variable light curve is that t = / c > t_ang. In this case t would be the duration of the burst and t_ang the variability time scale. This can be easily satisfied within internal shocks (see Fig 19). Consider an "inner engine" emitting a relativistic wind active over a time t = / c ( is the overall width of the flow in the observer frame). The source is variable on a scale L / c. Internal shocks will take place at R_s L ². At this place the angular time and the radial time satisfy: t_ang t_R L / c. Internal shocks continue as long as the source is active, thus the overall observed duration T = t reflects the time that the "inner engine" is active. Note that now t_ang L / c < t is trivially satisfied. The observed variability time scale in the light curve, t, reflects the variability of the source L / c. While the overall duration of the burst reflects the overall duration of the activity of the "inner engine".

Numerical simulations [193] have shown that not only the time scales are preserved but the source's temporal behavior is reproduced on an almost one to one basis in the observed light curve. This can be explained now [268] by a simple toy model (see Section VIB3 below).

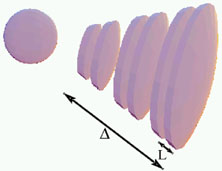Figure 19. The internal shocks model (from [364]) Faster. shells collide with slower ones and produce the observed rays. The variability time scale is L / c while the total duration of the burst is / c.

2. Caveats and Complications

Clearly the way to get around the previous argument is if t_ang < t_R. In this case one can identify t_R with the duration of the burst and t_ang as the variability time scale. The observed variability would require in this case that: t_ang / t_R = t / T. For this the emitting regions must be smaller than R / .

One can imagine an inhomogenous external medium which is clumpy on a scale d << R / (see Fig 20). Consider such a clump located at an angle ~ ^-1 to the direction of motion of the matter towards the observer. The resulting angular time, which is the difference in arrival time between the first and the last photons emitted from this clump would be: ~ d / c . Now t_ang ~ d / c < t_R and it seems that one can get around the argument presented before.

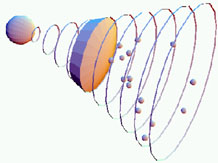Figure 20. The clumpy ISM model (from [364]). Note the small covering factor and the resulting "geometrical" inefficiency.

However, Sari and Piran [370] have shown that such a configuration would be extremely inefficient. This third part of this argument rules out this caveat. The observations limit the size of the clumps to d c t and the location of the shock to R cT ². The number of clumps within the observed angular cone with an opening angle ^-1 equals the number of pulses which is of the order T / t. The covering factor of the clumps can be directly estimated in terms of the observed parameters by multiplying the number of clumps (T / t) times their area d² = (t )² and dividing by the cross section of the cone (R / )². The resulting covering factor equals t / T << 1. The efficiency of conversion of kinetic energy to -rays in this scenario is smaller than this covering factor which for a typical variable burst could be smaller than 10^-2.

I turn now to several attempts to find a way around this result. I will not discuss here the feasibility of the suggested models (namely is it likely that the surrounding matter will be clumpy on the needed length scale [78], or can an inner engine eject "bullets" [162] with an angular width of ~ 10^-2 degrees and what keeps these bullets so small even when they are shocked and heated). I examine only the question whether the observed temporal structure can arise within these models.

3. External Shocks on a Clumpy Medium

Dermer and Mitman [78] claim that the simple efficiency argument of Sari and Piran [370] was flawed. They point out that if the direction of motion of a specific blob is almost exactly towards the observer the corresponding angular time will be of order d² / cR and not d / c used for a "generic" blob. This is narrower by a factor d / R than the angular time across the same blob that is located at a typical angle of ^-1. These special blobs would produce strong narrow peaks and will form a small region along a narrow cone with a larger covering factor. Dermer and Mitman [78] present a numerical simulation of light curves produced by external shocks on a clumpy inhomogeneous medium with t / T ~ 10^-2 and efficiency of up to ~ 10%.

A detailed analysis of the light curve poses, however, several problems for this model. While this result is marginal for bursts with t / T ~ 10^-2 with a modulation of 50% it is insufficient for bursts with t / T ~ 10^-3 or if the modulation is ~ 100%. Variability on a time scale of milliseconds has been observed [269] in many long GRBs (namely t / T can be as small as 10^-4). Moreover, in this case one would expect that earlier pulses (that arise from blobs along the direction of motion) would be narrower than latter pulses. This is not seen in the observed bursts [328].

Finally the arrival time of individual pulses depends on the position of the emitting clumps relative to the observers. Two following pulses would arise from two different clumps that are rather distant from each other. There is no reason why the pulses and intervals should be correlated in any way. Recall (Section IIA2) that the duration of a pulse and the subsequent interval are correlated [270].

4. The Shot-Gun Model

Heinz and Begelman [162] suggested that the "inner engine" operates as a shot-gun emitting multiple narrow bullets with an angular size much smaller than ^-1 (see Fig 21). These bullets do not spread while propagating and they are slowed down rapidly by an external shock with a very dense circumburst matter. The pulses width is given by t_ang or by the slowing down time. The duration of the burst is determined by the time that the "inner engine" emits the bullets.

Figure 21. The shot-gun model (from [364]). The inner engine emits narrow "bullets" that collide with the ISM.

This model can produce the observed variability and like in the internal shocks model the observed light curve represents also here the temporal activity of the source. However, in this model the width of the pulses is determined by the angular time or the hydrodynamic time or the cooling time of the shocked material. On the other hand the intervals between the pulses depend only on the activity of the inner engine. Again, there is no reason why the two distributions will be similar and why there should be a correlation between them (see Section IIA2 and [270]).

5. Relativistic Turbulence

An interesting alternative to shocks as a way to dissipate kinetic energy is within plasma turbulence [226, 227, 387, 388]. It has been suggested that in this case the kinetic energy of the shock is dissipated downstream to a combination of macroscopic (relativistic) random motion of plasma blobs with a Lorentz factor _b. Within these blobs the particles have also a (relativistic) random velocity with a Lorentz factor _p, such that: _{s b p}.

Relativistic turbulence may be the only way to produce variability in a situation that the matter is slowed down by the external medium and not by internal interaction. I stress that in this case the process is not described by regular shocks and hence some of the previous arguments do not hold. Two crucial open questions are i) Whether one can produce the observed correlations between pulses and intervals. ii) Why there is no spreading of pulses at later times, as would be expected if the emitting region is slowing down and increasing its radius.