4. PHYSICS OF ANISOTROPIES

The cosmological parameters affect the anisotropies through the well understood physics of the evolution of linear perturbations within a background FRW cosmology. There are very effective, fast, and publicly-available software codes for computing the CMB anisotropy, polarization, and matter power spectra, e.g., CMBFAST [14] and CAMB [15]. CMBFAST is the most extensively used code; it has been tested over a wide range of cosmological parameters and is considered to be accurate to better than the 1% level [16].

A description of the physics underlying the Cs can be separated into 3 main regions, as shown in Fig. 1.

Figure 1. Plot of the theoretical CMB anisotropy power spectrum, using a standard CDM model from CMBFAST. The x-axis is logarithmic here. The regions are labeled as in the text: the ISW Rise; Sachs-Wolfe Plateau; Acoustic Peaks; and Damping Tail. Also shown is the shape of the tensor (gravity wave) contribution, with an arbitrary normalization.

4.1. The Sachs-Wolfe plateau: 100

The horizon scale (or more precisely, the angle subtended by the Hubble radius) at last scattering corresponds to 100. Anisotropies at larger scales have not evolved significantly, and hence directly reflect the `initial conditions.' The combination of gravitational redshift and intrinsic temperature fluctuations leads to T / T (1/3) / c<sup>2</sup>, where is the perturbation to the gravitational potential. This is usually referred to as the `Sachs-Wolfe' effect [17].

Assuming that a nearly scale-invariant spectrum of density perturbations was laid down at early times (i.e., n 1, meaning equal power per decade in k), then ( + 1) C constant at low s. This effect is hard to see unless the multipole axis is plotted logarithmically (as in Fig. 1, but not Fig. 2).

Time variation in the potentials (i.e., time-dependent metric perturbations) leads to an upturn in the Cs in the lowest several multipoles; any deviation from a total equation of state w = 0 has such an effect. So the dominance of the Dark Energy at low redshift makes the lowest s rise above the plateau. This is sometimes called the `integrated Sachs-Wolfe effect' (or ISW Rise), since it comes from the line integral of 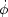. It has been confirmed through correlations between the large-angle anisotropies and large-scale structure [18]. Specific models can also give additional contributions at low (e.g., perturbations in the Dark Energy component itself [19]) but typically these are buried in the cosmic variance.

In principle, the mechanism that produces primordial perturbations would generate scalar, vector, and tensor modes. However, the vector (vorticity) modes decay with the expansion of the Universe. Tensors also decay when they enter the horizon, and so they contribute only to angular scales above about 1° (see Fig. 1). Hence some fraction of the low signal could be due to a gravity wave contribution, although small amounts of tensors are essentially impossible to discriminate from other effects that might raise the level of the plateau. However the tensors can be distinguished using polarization information (section 6).

4.2. The acoustic peaks: 100 1000

On sub-degree scales, the rich structure in the anisotropy spectrum is the consequence of gravity-driven acoustic oscillations occurring before the atoms in the universe became neutral. Perturbations inside the horizon at last scattering have been able to evolve causally and produce anisotropy at the last scattering epoch which reflects that evolution. The frozen-in phases of these sound waves imprint a dependence on the cosmological parameters, which gives CMB anisotropies their great constraining power.

The underlying physics can be understood as follows. When the proton-electron plasma was tightly coupled to the photons, these components behaved as a single `photon-baryon fluid', with the photons providing most of the pressure and the baryons the inertia. Perturbations in the gravitational potential, dominated by the dark matter component, are steadily evolving. They drive oscillations in the photon-baryon fluid, with photon pressure providing the restoring force. The perturbations are quite small, O(10^-5), and so evolve linearly. That means each Fourier mode evolves independently and is described by a driven harmonic oscillator, with frequency determined by the sound speed in the fluid. Thus, there is an oscillation of the fluid density, with velocity / 2 out of phase and having amplitude reduced by the sound speed.

After the Universe recombined the baryons and radiation decoupled, and the radiation could travel freely towards us. At that point the phases of the oscillations were frozen-in, and projected on the sky as a harmonic series of peaks. The main peak is the mode that went through 1/4 of a period, reaching maximal compression. The even peaks are maximal under-densities, which are generally of smaller amplitude because the rebound has to fight against the baryon inertia. The troughs, which do not extend to zero power, are partially filled because they are at the velocity maxima.

An additional effect comes from geometrical projection. The scale associated with the peaks is the sound horizon at last scattering, which can be confidently calculated as a physical length scale. This scale is projected onto the sky, leading to an angular scale that depends on the background cosmology. Hence the angular position of the peaks is a sensitive probe of the spatial curvature of the Universe (i.e., _tot), with the peaks lying at higher in open universes and lower in closed geometry.

One last effect arises from reionization at redshift z_i. A fraction of photons will be isotropically scattered at z < z_i, partially erasing the anisotropies at angular scales smaller than those subtended by the Hubble radius at z_i. This corresponds typically to s above about a few 10s, depending on the specific reionization model. The acoustic peaks are therefore reduced by a factor e^-2 relative to the plateau.

These acoustic peaks were a clear theoretical prediction going back to about 1970 [20]. Their empirical existence started to become clear around 1994 [21], and the emergence, over the following decade, of a coherent series of acoustic peaks and troughs is a triumph of modern cosmology. One can think of these peaks as a snapshot of stochastic standing waves. And, since the physics governing them is simple, then one can see how they encode information about the cosmological parameters.

4.3. The damping tail: 1000

The recombination process is not instantaneous, giving a thickness to the last scattering surface. This leads to a damping of the anisotropies at the highest s, corresponding to scales smaller than that subtended by this thickness. One can also think of the photon-baryon fluid as having imperfect coupling, so that there is diffusion between the two components, and the oscillations have amplitudes that decrease with time. These effects lead to a damping of the Cs, sometimes called Silk damping [22], which cuts off the anisotropies at multipoles above about 2000.

An extra effect at high s comes from gravitational lensing, caused mainly by non-linear structures at low redshift. The Cs are convolved with a smoothing function in a calculable way, partially flattening the peaks, generating a power-law tail at the highest multipoles, and complicating the polarization signal [23]. This is an example of a `secondary effect', i.e., the processing of anisotropies due to relatively nearby structures. Galaxies and clusters of galaxies give several such effects, but all are expected to be of low amplitude and are typically only important for the highest s.