Astronomers have long relied on photometry to yield estimates on
mass, specifically through well defined mass to luminosity ratios
(M / L). This is not at all surprising, since visual astronomy
relies on the light emitted from distant objects. For example,
the M / L ratio for the sun is M / L = 5.1
× 103 kg/W; since this number is not terribly
instructive, one usually measures mass to luminosity in terms of
the sun's mass and luminosity such that
M
/
L = 1 by
definition. Thus by measuring the light output of an object (for
example a galaxy or cluster of galaxies) one can use well-defined
M / L ratios in order to estimate the mass of the object.
In the early 1930s, J. H. Oort found that the motion of stars in the Milky Way hinted at the presence of far more galactic mass than anyone had previously predicted. By studying the Doppler shifts of stars moving near the galactic plane, Oort was able to calculate their velocities, and thus made the startling discovery that the stars should be moving quickly enough to escape the gravitational pull of the luminous mass in the galaxy. Oort postulated that there must be more mass present within the Milky Way to hold these stars in their observed orbits. However, Oort noted that another possible explanation was that 85% of the light from the galactic center was obscured by dust and intervening matter or that the velocity measurements for the stars in question were simply in error. [1]
Around the same time Oort made his discovery, Swiss astronomer
F. Zwicky found similar indications of missing mass, but on a much
larger scale. Zwicky studied the Coma cluster, about 99 Mpc (322
lightyears) from Earth, and, using observed doppler shifts in
galactic spectra was able to calculate the velocity dispersion of
the galaxies in the Coma cluster. Knowing the velocity dispersions
of the individual galaxies (i.e. kinetic energy), Zwicky employed
the virial theorem to calculate the cluster's mass. Assuming only
gravitational interactions and Newtonian gravity (F
1 /
r2), the virial theorem gives the following relation
between kinetic and potential energy:
 |
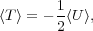(1) |
where < T > is the average kinetic energy and
< U > is the average potential energy. Zwicky found
that the average mass of one nebula within the Coma cluster is
Mnebula = 4.5 × 1010
M, with
about a thousand nebula in the cluster (so the total mass of the cluster
Mcluster
4.5 ×
1013
M). This
result was startling because a measurement of the luminosity of the cluster
using standard M / L ratios for clusters gave a mass
approximately 10% of this value. In essence, galaxies only accounted for
about two percent of the total mass with intracluster gas contributing
another ten percent; the vast majority of the mass of the Coma
cluster was for some reason non-luminous.
[2<>]
Roughly 40 years following the discoveries of Oort, Zwicky, and others, Vera Rubin and collaborators conducted an extensive study of the rotation curves of 60 isolated galaxies. [3] The galaxies chosen were oriented in such a way so that material on one side of the galactic nucleus was approaching our galaxy while material on the other side was receding; thus the analysis of spectral lines (Doppler shift) gave the rotational velocity of regions of the target galaxy. Additionally, the position along the spectral line gave angular information about the distance of the point from the center of the galaxy. Ideally one would target individual stars to determine their rotational velocities; however, individual stars in distant galaxies are simply too faint, so Rubin used clouds of gas rich in hydrogen and helium that surround hot stars as tracers of the rotational profile.
It was assumed that the orbits of stars within a galaxy would closely mimic the rotations of the planets within our solar system. Within the solar system,
 |
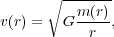(2) |
where v(r) is the rotation speed of the object at a
radius r, G is the gravitational constant, and
m(r) is the
total mass contained within r (for the solar system essentially
the sun's mass), which is derived from simply
setting the gravitational force equal to the centripetal force
(planetary orbits being roughly circular). Therefore, v(r)
1/ r1/2, meaning that the velocity of a rotating body
should decrease as its distance from the center increases, which is
generally referred to as "Keplerian" behavior.
Rubin's results showed an extreme deviation from predictions due to Newtonian gravity and the luminous matter distribution. The collected data showed that the rotation curves for stars are "flat," that is, the velocities of stars continue to increase with distance from the galactic center until they reach a limit (shown in Fig. 1). An intuitive way to understand this result is to apply Gauss's law for gravity (in direct analogy with Gauss's Law for the electric field):
 |
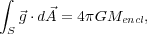(3) |
where the left hand side is the flux of the gravitational field through a closed surface and the right hand side is proportional to the total mass enclosed by that surface. If as the radius of the Gaussian surface increases more and more mass in enclosed, then the gravitational field will grow, leading to a larger rotational velocity. If, however, the mass enclosed decreases or remains constant as the Gaussian surface grows, then the gravitational field will fall, leading to smaller and smaller rotational velocities. Near the center of the galaxy where the luminous mass is concentrated falls under the former condition, whereas in the outskirts of the galaxy where little to no additional mass is being added (the majority of the galaxy's mass being in the central bulge) one expects the situation to be that of the latter. Therefore, if the rotational velocities remain constant with increasing radius, the mass interior to this radius must be increasing. Since the density of luminous mass falls past the central bulge of the galaxy, the "missing" mass must be non-luminous. Rubin summarized, "The conclusion is inescapable: mass, unlike luminosity, is not concentrated near the center of spiral galaxies. Thus the light distribution in a galaxy is not at all a guide to mass distribution." [3]
 |
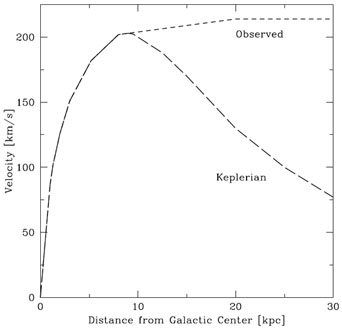Figure 1. An example of how rotation curves were expected to behave (Keplerian: long dashed line) and how they actually behave (Observed: short dashed line). |
In the 1970s, another way to probe the amount and distribution of dark matter was discovered: gravitational lensing. Gravitational lensing is a result of Einstein's Theory of Relativity which postulates that the universe exists within a flexible fabric of spacetime. Objects with mass bend this fabric, affecting the motions of bodies around them (objects follow geodesics on this curved surface). The motions of planets around the sun can be explained in this way, much like how water molecules circle an empty drain. The path of light is similarly affected; light bends when encountering massive objects. To see the effects of gravitational lensing, cosmologists look for a relatively close, massive object (often a cluster of galaxies) behind which a distant, bright object (often a galaxy) is located. If the distant galaxy were to be located directly behind the cluster, a complete "Einstein ring" would appear; this looks much like a bullseye, where the center is the closer object and the ring is the lensed image of the more distant object. However, the likelihood of two appropriately bright and distant objects lining up perfectly with the Earth is low; thus, distorted galaxies generally appear as "arclets," or partial Einstein rings.
In 1979, D. Walsh et al. were among the first to observe gravitational lensing. Working at the Kitt Peak National Observatory, they found two distant objects separated by only 5.6 arc seconds with very similar redshifts, magnitudes, and spectra. [4] They concluded that perhaps they were seeing the same object twice, due to the lensing of a closer, massive object. Similar observations were made by R. Lynds and V. Petrosian in 1988, in which they saw multiple arclets within clusters. [5]
We can study a distant galaxy's distorted image and make conclusions
about the amount of mass within a lensing cluster using this expression for
e, the
"Einstein radius" (the length of an arclet in radians):
 |
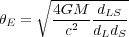(4) |
where G is the gravitational constant, M is the mass of the lens, c is the speed of light,and dLS, dL, and dS are the distance between the lens and source, the distance to the lens, and the distance to the source, respectively. Physicists have found that this calculated mass is much larger than the mass that can be inferred from a cluster's luminosity. For example, for the lensing cluster Abell 370, Bergmann, Petrosian, and Lynds determined that the M / L ratio of the cluster must be about 102 - 103 solar units, necessitating the existence of large amounts of dark matter in the cluster as well as placing constraints on its distribution within the cluster. [6]