3. THE REIONIZATION PROCESS

The inflationary process that occurred very early in the Universe has created the initial tiny fluctuations in matter density field. The high density peaks in these fluctuations field are the seeds around which galaxies form. The formation process is initially driven by gravitational instability alone but later gas physics, cooling, heating, radiation processes and feedback effects play an important role as well [132, 156]. The first galaxies form when primordial gas (H Iand He I) condenses within dark matter potential wells which leads to radiative cooling driven mostly by the Lyman line transition [53, 75, 107, 106, 105, 153] and, probably, by H₂ cooling. To date Lyman emission has been observed in many high redshift galaxies [98, 140, 149, 150]. This gas condenses further to form the first stars and black holes which in turn produce radiation that starts ionizing the Universe. The efficiency with which these objects produce ionizing radiation is subject to many different physical processes and assumptions (see e.g., [44]). Since this book's topic is the first galaxies, the reader is referred to the other chapters in this volume for detailed discussion of how the first radiation emitting objects form and how efficient are they in producing ionizing radiation.

An important unknown in these galaxies is the so called escape fraction, namely the fraction of ionizing radiation that escapes the galaxy into the IGM. It is these ionizing photons that are relevant to the Universe's reionization. Determining the escape fraction of ionizing radiation observationally is very difficult especially at high redshifts where the available information is very limited. Nevertheless, such observations have been carried out by a number of authors [70, 91, 92, 181, 189] where the measured fraction is found to be between 0.1-0.5. Theoretical prediction of the escape fraction is also difficult. Early studies have assumed idealized smooth galaxies [55, 56, 167, 214] but later studies have simulated more realistic galaxies (see e.g., [43]). Each of these studies have considered different set up and different sources but all conclude that the escape fraction of radiation is roughly in the range of 0.1-0.5.

The most accepted picture of how reionization unfolds is simple. The first radiation-emitting objects ionize their immediate surroundings, forming bubbles that expand until their ionizing photons are consume by the neutral IGM. As the number of radiating sources increases, so do the number and size of the ionization bubbles, which eventually spread to fill the whole Universe. However, most of the details of this scenario are yet to be clarified. For example: what controls the formation of the first objects and how much ionizing radiation do they produce? How do the bubbles expand into the intergalactic medium and what do they ionize first, high-density or low density regions? The answer to these important questions and many others touch upon many fundamental questions in cosmology, galaxy formation, quasars activity and the physical properties of very metal poor stars [9, 30, 44, 41, 67, 135].

To ionize hydrogen one needs photons with energy of 13.6 eV or higher meaning the reionization of the Universe requires ultraviolet photons. A crucial question is which sources in the Universe provide the UV photons needed to ionize the Universe and maintain it in that state. Obvious candidates are the first stars (so called Population III stars), second generation stars (Population II stars) and (mini)quasars which are objects powered by intermediate mass black holes (10^3-6 M). There are other candidate sources of reionization, like decaying or self-annihilating dark matter particles or decaying cosmic strings. However, the constraints on such objects make it unlikely that they could reionize the Universe by themselves [40, 100, 121, 122, 142, 151, 168, 231].

Massive black holes powering quasars convert mass to radiation extremely efficiently. They produce a large amount of UV and X-ray radiation above the ionization threshold. In fact, one of the main discoveries of the last decade is that quasars, powered by very large black holes with masses in excess of 10⁹ M, already existed at redshift above 7 (e.g., QSO ULAS J1120+0641 [137] from the UKIDSS survey [108]). How these black holes managed to accumulate so much mass in such a short time is a puzzle in its own right [137, 20]. However, the mass distribution of the massive black holes in the early Universe is unknown, rendering the role played by quasars during reionization very uncertain.

Population III stars formed from the primordial mix of the elements and thus only contain hydrogen and helium. This composition makes them very different from present-day stars. In order for a star to form, the initial proto-star has to radiate some of the energy gained by gravitational contraction, or the collapse will rapidly halt as the cloud reaches hydrostatic equilibrium. Population III stars are poor radiators until the cloud from which they form reaches high temperatures. This causes them to be very massive, and hence, they are very efficient and abundant sources of UV photons, yet are very short lived. Theoretically, these objects could have reionized the Universe but our knowledge of them, including the question of whether they existed in sufficient numbers, is very uncertain.

The first stars' early metal enrichment was likely the dominant effect that brought about the transition from Population III to Population II star formation. Recent numerical simulations of collapsing primordial objects with masses of ≈ 10⁶ M, have shown that the gas has to be enriched with heavy elements to a minimum level of Z_crit ≈ 10^-4 Z, in order to have any effect on the dynamics and fragmentation properties of the system. Normal, low-mass (Population II) stars are hypothesized to form only out of gas with metallicity Z ≥ Z_crit. Thus, the characteristic mass scale for star formation is expected to be a function of metallicity, with a discontinuity at Z_crit where the mass scale changes by about two orders of magnitude. The redshift where this transition occurs has important implications for the early growth of cosmic structure, and the resulting observational signature includes the extended nature of reionization (see the review by Ciardi and Ferrara [44]).

Most studies of reionization have focused on stars as being the primary source [126, 1, 2, 29, 221]. Due to the deficiency of hard photons in the spectral energy distributions (SEDs) of these "first stars", heating due to these objects is limited in extent [204]. On the other hand, miniquasars (miniqsos), characterized by central black hole masses < 10⁶ M, have also been considered as an important contributor to reionization [120, 165, 166, 144, 66, 69, 217, 204]. Ionization aspects of the miniquasar radiation have been explored by several authors [120, 165, 166, 204, 206, 229]. Thomas & Zaroubi [204] have shown that although the ionization pattern around miniqsos is similar to that of stellar-type sources, the heating due to the presence of hard photons in miniqsos is very different. The reason being is that stars produce thermal radiation that is mostly in the UV range, which is very efficient in ionization, but once it is absorbed by H I, the energy left will be too small to be converted to heat effectively. On the other hand black hole powered sources have hard x-ray photons as their spectral energy distribution (SED) follows a power law (typically assumed to be -1). Such x-ray photons have lower bound-free cross section relative to UV photons but once they are absorbed, their leftover energy is very large and can easily be converted to heat. Also, x-ray photons penetrate much deeper into the IGM and can heat it up much further from the source than UV radiation.

Miniqsos heat the surrounding IGM well beyond their ionization front [204, 42]. Several authors (e.g., [120, 144, 230] have shown the importance of heating the IGM with respect to the observability of the redshifted 21 cm radiation in either emission or absorption. Figure 13 shows the ionization and heating patterns around a number of stars (upper panels) and miniqsos (lower panel). The mass of the stars and black-holes are indicated next to the lines, and their SEDs are assumed to be thermal or to have a power law dependence on the photon energy, ∝ E^-1, respectively. The calculation here is spherically symmetric and assumes a single object forming in the IGM [230, 204]. The ionization pattern around stars and black holes are very similar, they both show a very abrupt increase in H I with a clear ionization front (see e.g. [102, 204, 230]). Of course the radius at which such front is seen depends on the mass of the star or the black hole but the pattern is the same (see the left hand side panels of Figure 13). The heating profile around the two types of sources, on the other hand, is different since in power law sources (miniqsos) the radiation can penetrate the neutral gas and reach large distances from the sources (see right hand panels of Figure 13). This high energy radiation is efficient in heating the IGM gas through secondary electrons [183] (see discussion later) whereas UV radiation is efficient in ionizing the gas but has little energy left to heat too much and can not penetrate the neutral gas as far as x-ray radiation does.

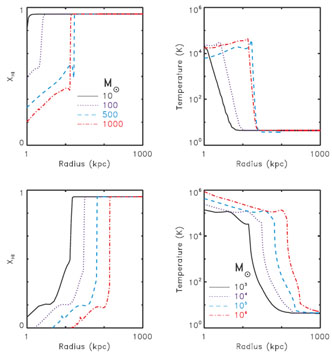Figure 13. This figure shows the ionization and heating profile around a single star and black hole forming in the IGM assuming spherical symmetry. The upper panels show the stars case whereas the lower panels show the black holes case. The left hand panels show the neutral fraction of H I as a function of distance from the star and the right hand panels show the gas temperature as a function of distance from the source [204].

We have seen that unlike stars, x-ray source a (e.g., miniquasars) have an additional property of heating the IGM to a large extent and through secondary Lyman radiation making the neutral IGM visible to a 21-cm experiment. However, some authors (e.g., [52, 175]) argue that miniquasars alone can not reionize the Universe as they will produce far more soft X-ray background radiation than currently observed [136, 186] while simultaneously satisfying the WMAP3 polarisation results [152, 187]. It should be noted, however, that these calculations have been carried out assuming specific models for the evolution of black hole mass density and spectral energy distributions of UV/X-ray radiation of the miniquasars, whereas one can easily construct other models in which the discrepancy is not so severe [230, 169].

Some authors [99] have claimed a detection of excess IR background radiation and argued that it provides evidence for stars being the primary source of reionization. This too has been subject to controversy because of the sensitivity of the result to the subtraction of the contaminants, e.g., Zodiacal light, within the same waveband [48].

Although uncertainty looms about the sources that resided during the dark ages, it is conceivable from observations of our Universe up to redshifts of 6.5, that sources of reionization could have been a mixture of both stellar and miniquasar sources. Implementing radiative transfer that includes both ionizing and hard X-ray photons has been difficult and, as a result, most 3-D radiative transfer schemes restrict themselves to ionization due to stars [12, 45, 73, 126, 127, 141, 154, 170, 163, 196, 211, 222]. In [165], a "semi" hybrid model of stars and quasars like the one hinted above used, albeit in sequential order instead of a simultaneous implementation. That is, pre-ionization due to quasars has been invoked between 7 ≤ z ≤ 20, after which stars reionize the Universe at redshift 7.

Given the numerical cost of the full 3D radiative transfer schemes, exploring a large parameter space for models of reionization, is not feasible. Such an exploration is needed in order to understand the various physical effects introduced by each such parameter. It is also needed to help interpret the available data. A number of authors have been pursuing "quick-and-dirty" methods to simulate the reionization process. These schemes can include very rough methods that use the initial density field to produce a reionization cube without the need for cosmological N-body and hydro simulations, such as 21cmFAST ([129, 222, 223]) and SimFast21 [177]. They also include more accurate (yet still fast) methods like BEARS [204, 206, 205] that use N-body and hydro simulations but reduces the numerical cost by restricting the ionization bubbles around the radiation sources to be spherical.