


To date, the majority of observations related to the EoR provide weak and model dependent constraints on reionization. However, there are currently a number of observations which could impose strong constraints on reionization models, as discussed below. It should be noted however that none of these observations constrains the EoR evolution in detail.
2.1. The Lyman
 forest at z ≈
2.5-6.5
forest at z ≈
2.5-6.5
The state of the intergalactic medium (IGM) can be studied through the
analysis of the Lyman- forest. This is an absorption phenomenon seen in the spectra
of background quasi-stellar objects (QSOs). The history of this field
goes back to 1965 when a number of authors
[74,
179]
predicted that an expanding Universe, homogeneously filled with gas, will
produce an absorption trough due to neutral hydrogen, known as the
Gunn-Peterson trough, in the spectra of distant QSOs bluewards of the
Lyman-
forest. This is an absorption phenomenon seen in the spectra
of background quasi-stellar objects (QSOs). The history of this field
goes back to 1965 when a number of authors
[74,
179]
predicted that an expanding Universe, homogeneously filled with gas, will
produce an absorption trough due to neutral hydrogen, known as the
Gunn-Peterson trough, in the spectra of distant QSOs bluewards of the
Lyman- emission line of
the quasar. That is, the quasar flux will be absorbed at the UV
resonance line frequency of 1215.67 Å. Gunn & Peterson
[74]
found such a spectral region of reduced flux, and used this measurement to
put upper limits on the amount of intergalactic neutral hydrogen. The
large cross-section for the Lyman
emission line of
the quasar. That is, the quasar flux will be absorbed at the UV
resonance line frequency of 1215.67 Å. Gunn & Peterson
[74]
found such a spectral region of reduced flux, and used this measurement to
put upper limits on the amount of intergalactic neutral hydrogen. The
large cross-section for the Lyman
 absorption makes this
technique very powerful for studying gas in the intergalactic medium.
absorption makes this
technique very powerful for studying gas in the intergalactic medium.
In the last 15 years two major advances occurred. The first was the development of high-resolution echelle spectrographs on large telescopes (e.g., HIRES on the Keck and UVES on the Very Large Telescope) that provided data of unprecedented quality. The second was the emergence of a theoretical paradigm within the context of cold dark matter (CDM) cosmology that accounts for all the features seen in these systems (e.g. [16, 39, 81, 118, 131, 201, 232, 233]). According to this paradigm, the absorption is produced by volume filling photoionized gas that contains most of the baryons at redshifts at z ~ 3-6 and resides in mildly non-linear overdensities.
Figure 3 shows a typical example of the Lyman
 forest seen in the
spectrum of the z = 3.12 quasar
Q0420-388. An interesting feature of such spectra is
the density of weak
absorbing lines which increase with redshift due to the expansion of the
Universe. In fact, at redshifts above 4, the density of the absorption
features become so high that it is hard to define them as separate
absorption features. Instead, one sees only the flux in between the
absorption minima which appears as if they are emission rather than
absorption lines.
forest seen in the
spectrum of the z = 3.12 quasar
Q0420-388. An interesting feature of such spectra is
the density of weak
absorbing lines which increase with redshift due to the expansion of the
Universe. In fact, at redshifts above 4, the density of the absorption
features become so high that it is hard to define them as separate
absorption features. Instead, one sees only the flux in between the
absorption minima which appears as if they are emission rather than
absorption lines.
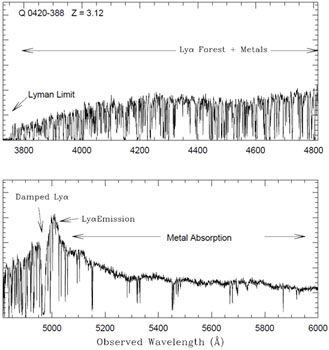 |
Figure 3. High resolution spectrum of the
z = 3.12 quasar Q0420-388 obtained with the Las Campanas
echelle spectrograph by J. Bechtold and S. A. Shectman. The two panels
cover the whole wavelength range of the spectrum. The Lyman
|
The Lyman  forest has
turned out to be a treasure trove for
studying the intergalactic medium and its properties in both low and
high density regions. In particular, it is very sensitive to the neutral
hydrogen column density and hence, to the neutral fraction as a function
of redshift along the line of sight. In the following, we demonstrate
how one could constrain the neutral fraction of hydrogen from the forest
and what the values obtained from the data are. For a review on the
Lyman
forest has
turned out to be a treasure trove for
studying the intergalactic medium and its properties in both low and
high density regions. In particular, it is very sensitive to the neutral
hydrogen column density and hence, to the neutral fraction as a function
of redshift along the line of sight. In the following, we demonstrate
how one could constrain the neutral fraction of hydrogen from the forest
and what the values obtained from the data are. For a review on the
Lyman  forest the reader
is referred to
[162].
forest the reader
is referred to
[162].
We need to calculate the optical depth for absorption of
Lyman  photons. A photon
emitted by a distant quasar with an energy higher than 10.196 eV is
continuously redshifted as it travels through the
intergalactic medium until it reaches the observer. At some
intermediate point the photon is redshifted to around 1216 Å in
the rest-frame of the intervening medium, which may contain neutral
hydrogen. It can then excite the
Lyman
photons. A photon
emitted by a distant quasar with an energy higher than 10.196 eV is
continuously redshifted as it travels through the
intergalactic medium until it reaches the observer. At some
intermediate point the photon is redshifted to around 1216 Å in
the rest-frame of the intervening medium, which may contain neutral
hydrogen. It can then excite the
Lyman  transition and be
absorbed. Let us consider a particular line of sight from the observer
to the quasar. The optical depth
transition and be
absorbed. Let us consider a particular line of sight from the observer
to the quasar. The optical depth

 of a
photon is related to the probability of the photon's
transmission e-
of a
photon is related to the probability of the photon's
transmission e-
 . At a given observed frequency,
. At a given observed frequency,
 0, the
Lyman
0, the
Lyman  optical depth is
given by
optical depth is
given by
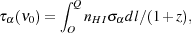 |
(1) |
where l is the comoving radial coordinate of some
intermediate point along the line of sight, z is the redshift and
nHI is the proper number density of neutral hydrogen
at that point. The limits of the integration, O and Q, are
the comoving distance between the observer and the quasar,
respectively. The Lyman  absorption cross section is denoted by
absorption cross section is denoted by

 . It is a
function of the frequency of the photon,
. It is a
function of the frequency of the photon,
 , with respect to the
rest-frame
of the intervening H I at position l. The
cross section is peaked when
, with respect to the
rest-frame
of the intervening H I at position l. The
cross section is peaked when  is equal to
the Lyman
is equal to
the Lyman  frequency
frequency

 .
The frequency
.
The frequency  is related to
the observed frequency
is related to
the observed frequency
 0 by
0 by
 =
=
 0(1 + z),
where 1 + z is the
redshift factor due to the uniform Hubble expansion alone at the same
position. Note that for the sake of simplicity here we ignore peculiar
velocity effects.
0(1 + z),
where 1 + z is the
redshift factor due to the uniform Hubble expansion alone at the same
position. Note that for the sake of simplicity here we ignore peculiar
velocity effects.
Using dl = c dt / a, where a is the Hubble scale factor and t is the proper time and Friedmann equation for a flat Universe with cosmological constant, we have,
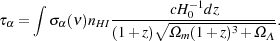 |
(2) |
This optical depth should also
depend on the Lyman  line profile function but here we assume that it is basically
a
line profile function but here we assume that it is basically
a  -function centered at
the frequency
-function centered at
the frequency  . Considering
nHI = nH xHI,
where xHI is the neutral fraction of hydrogen, and
integrating over this equation, one obtains the following result:
. Considering
nHI = nH xHI,
where xHI is the neutral fraction of hydrogen, and
integrating over this equation, one obtains the following result:
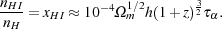 |
(3) |
Since the Lyman  features mostly show mild absorption probability
(
features mostly show mild absorption probability
(

 1) this equation
clearly implies that at the mean density of the Universe at
1) this equation
clearly implies that at the mean density of the Universe at

 of
about one the ionized fraction is on the order of 10-4.
Therefore, the fact that we observe the Lyman
of
about one the ionized fraction is on the order of 10-4.
Therefore, the fact that we observe the Lyman
 forest at all means
that the Universe is highly ionized at least until z ≈
6. This is the
most reliable and robust evidence that the Universe has in fact reionized.
forest at all means
that the Universe is highly ionized at least until z ≈
6. This is the
most reliable and robust evidence that the Universe has in fact reionized.
Another important evidence relevant for reionization comes from high
resolution spectroscopy of high redshift Sloan Digital
Sky Survey (SDSS) quasars
[59,
60].
The SDSS has discovered about 19 QSOs
with redshifts around 6 that are powered by black holes with masses on
the order of 109
M .
In a follow up observations with 10 meter class telescopes Fan et al.
[59,
60]
were able to obtain high resolution spectra of these objects.
.
In a follow up observations with 10 meter class telescopes Fan et al.
[59,
60]
were able to obtain high resolution spectra of these objects.
Fig. 4 shows the spectra of these high redshift
quasars
[59,
60].
Notice the complete absence of structure that some of these spectra
exhibit bluewards of the quasar Lyman
 restframe emission,
especially those with redshift z
restframe emission,
especially those with redshift z
 6.
This is normally attributed to an increase in
6.
This is normally attributed to an increase in

 as a
result of the decrease in the ionized fraction of the Universe. Notice
also, that although the trend with redshift is clear, it is by no means
monotonic. For example, quasar J1411+3533 at z = 5.93
shows an "emptier" trough relative to quasars J0818+1722 at z =
6. Such trend might be indicating
a more patchy ionization of the IGM at such redshifts.
as a
result of the decrease in the ionized fraction of the Universe. Notice
also, that although the trend with redshift is clear, it is by no means
monotonic. For example, quasar J1411+3533 at z = 5.93
shows an "emptier" trough relative to quasars J0818+1722 at z =
6. Such trend might be indicating
a more patchy ionization of the IGM at such redshifts.
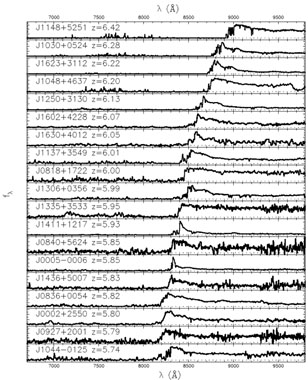 |
Figure 4. Spectra for high redshift SDSS
quasars. The Gunn-Peterson trough bluewards of the QSO
Lyman |
Figure 5 shows the effective Lyman
 or Gunn-Peterson
optical depth,
or Gunn-Peterson
optical depth,
 GPeff,
as a function of redshift as estimated from the joint optical depths of
Lyman
GPeff,
as a function of redshift as estimated from the joint optical depths of
Lyman  ,
,
 and
and  . From
this plot it is clear that the increase in the optical depth as a
function of redshift is much larger than expected (shown in the dashed
line) from passive redshift evolution of the density of the Universe.
. From
this plot it is clear that the increase in the optical depth as a
function of redshift is much larger than expected (shown in the dashed
line) from passive redshift evolution of the density of the Universe.
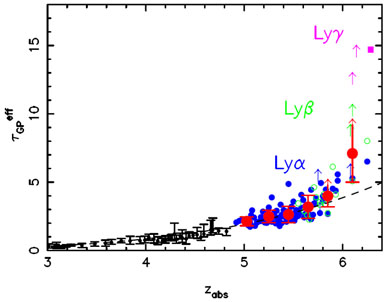 |
Figure 5. Evolution of the
Lyman |
The interpretation of the increase in the optical depth at z
 6.3 has been the subject of some debate. All authors agree that this
is a sign of an increase in the Universe's neutral fraction at high
redshifts, marking the tail end of the reionization process. The
controversy is centered on the question of by how much the neutral
fraction increases. Some authors
[217,
218,
130]
have argued that the size of the so call Near Zone ionized by the quasar
itself and set redwards of the Gunn-Peterson trough indicates that the
neutral fraction around the SDSS high redshift quasars is ≈
10%. More recently is had been suggested that the
variations seen across various SDSS quasars indicate that the
ionization state of the IGM at these redshifts changes significantly
across different sightlines
[128].
However, given the intense radiation field around these quasars, it is not
possible to put general constraints on the neutral fraction of the IGM
from quasars at redshift below 6.5 (see e.g.,
[18,
216,
123,
124]).
Moreover, recently and with the discovery of the redshift
z = 7.1 QSO ULAS J1120+0641
[137]
by the UKIDSS survey
[108]
it has been argued that this quasar's Near Zone gives a clear evidence
for an increase in the neutral fraction of hydrogen in the IGM at
z = 7.1
[137,
20].
Note however that his conclusion relies on one quasar
and might change as more of such quasars at z
6.3 has been the subject of some debate. All authors agree that this
is a sign of an increase in the Universe's neutral fraction at high
redshifts, marking the tail end of the reionization process. The
controversy is centered on the question of by how much the neutral
fraction increases. Some authors
[217,
218,
130]
have argued that the size of the so call Near Zone ionized by the quasar
itself and set redwards of the Gunn-Peterson trough indicates that the
neutral fraction around the SDSS high redshift quasars is ≈
10%. More recently is had been suggested that the
variations seen across various SDSS quasars indicate that the
ionization state of the IGM at these redshifts changes significantly
across different sightlines
[128].
However, given the intense radiation field around these quasars, it is not
possible to put general constraints on the neutral fraction of the IGM
from quasars at redshift below 6.5 (see e.g.,
[18,
216,
123,
124]).
Moreover, recently and with the discovery of the redshift
z = 7.1 QSO ULAS J1120+0641
[137]
by the UKIDSS survey
[108]
it has been argued that this quasar's Near Zone gives a clear evidence
for an increase in the neutral fraction of hydrogen in the IGM at
z = 7.1
[137,
20].
Note however that his conclusion relies on one quasar
and might change as more of such quasars at z
 7 are discovered.
7 are discovered.
There are more things that we can learn about reioinzation from the
Lyman  forest that we
will discuss later. But to summarize, the main conclusion from the
Lyman
forest that we
will discuss later. But to summarize, the main conclusion from the
Lyman  optical
depth measurements is
that the Universe is highly ionized at redshifts below 6 (as seen in
Figure 4), while at about z = 6.3, the its neutral
fraction increases, forming the tail end of the
reionization process (see Figure 5) .
optical
depth measurements is
that the Universe is highly ionized at redshifts below 6 (as seen in
Figure 4), while at about z = 6.3, the its neutral
fraction increases, forming the tail end of the
reionization process (see Figure 5) .
2.2. The Thomson Scattering Optical depth for the Cosmic Microwave Background (CMB) Radiation
This is a very evolved topic, discussed and reviewed by many authors (e.g., [157, 195, 21, 117, 86, 4]). Here, I give a general review of the constraints provided by the CMB on reionization. The CMB provides important information relevant to the history of reionization. It is known that the Universe has indeed recombined and became largely neutral at z ≈ 1100. If recombination had been absent or substantially incomplete, the resulting high density of free electrons would imply that photons could not escape Thomson scattering until the density of the Universe dropped much further. This scattering would inevitably destroy the correlations at subhorizon angular scales seen in the CMB data (see e.g., [85, 190]).
In order to calculate the effect of reionization on CMB photons, a function is often defined called the visibility function 1,
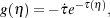 |
(4) |
where  (≡ ∫
dt / a ) is the conformal time, a is the scale
factor of the Universe and
(≡ ∫
dt / a ) is the conformal time, a is the scale
factor of the Universe and
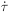 is the derivative
of the optical depth with respect to to
is the derivative
of the optical depth with respect to to
 . The
optical depth for Thomson scattering is
given by
. The
optical depth for Thomson scattering is
given by  (
( ) =
-∫
) =
-∫
 0
d
0
d
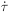 =
∫
=
∫
 0 d
0 d a(
a( )
ne
)
ne
 T, where
T, where
 0
is the present time, ne is the
electron density and
0
is the present time, ne is the
electron density and
 T is the
Thomson cross section. The visibility
function gives the probability density that a photon
had scattered out of the line of sight between
T is the
Thomson cross section. The visibility
function gives the probability density that a photon
had scattered out of the line of sight between
 and
and
 +
d
+
d . The influence of reionization on the
CMB temperature fluctuations is obtained by integrating Equation 4 along
each sightline to estimate the temperature fluctuation suppression due
to the EoR. The suppression probability turns out to be
roughly proportional to 1 -
e-
. The influence of reionization on the
CMB temperature fluctuations is obtained by integrating Equation 4 along
each sightline to estimate the temperature fluctuation suppression due
to the EoR. The suppression probability turns out to be
roughly proportional to 1 -
e- [224].
Since the amount of suppression in the measured power spectrum is small, the
optical depth for Thomson scattering must be small too
[152].
The left hand panel in Figure 6 shows the
influence of increasing the value of
[224].
Since the amount of suppression in the measured power spectrum is small, the
optical depth for Thomson scattering must be small too
[152].
The left hand panel in Figure 6 shows the
influence of increasing the value of
 , the Thomson
optical depth, on the CMB
temperature fluctuation power spectrum. The right hand panel shows the
reionization history of the Universe assumed in the left panel. Since in
this case a sudden global reionization is assumed,
there is one to one correspondence between the optical depth for Thomson
scattering and the redshift of reionization.
, the Thomson
optical depth, on the CMB
temperature fluctuation power spectrum. The right hand panel shows the
reionization history of the Universe assumed in the left panel. Since in
this case a sudden global reionization is assumed,
there is one to one correspondence between the optical depth for Thomson
scattering and the redshift of reionization.
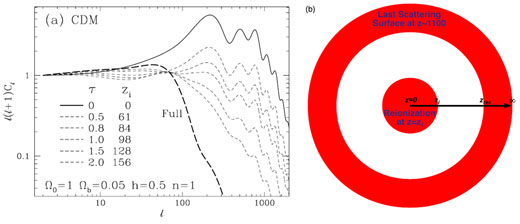 |
Figure 6. Left hand panel (a): The
influence of reionization on the CMB temperature angular power
spectrum. Reionization damps anisotropy power
as e-2 |
Further information can be obtained from observations of CMB via the polarization power spectrum. The polarization of the CMB emerges naturally from the Cold Dark Matter paradigm which stipulates that small fluctuations in the early universe grow, through gravitational instability, into the large scale structure we see today ([21, 86, 97, 227]). Since, the temperature anisotropies observed in the CMB are the result of primordial fluctuations, they would naturally polarize the CMB anisotropies. The degree of linear polarization of the CMB photons at any scale reflects the quadrupole anisotropy in the plasma when they last scattered at that same scales. From this argument it is clear that the amount of polarization at scales larger than the horizon scale at the last scattering surface should fall down since there is no more coherent quadrupole contribution due to the lack of causality. This is shown in the sketch presented in the left hand panel in Figure 7. The largest scale at which a primordial quadrupole exists is the scale of the horizon at recombination, which roughly corresponds to 1°. Therefore, any polarization signature on scales larger than the horizon scale provides a clear evidence for Thomson scattering at later stages where the horizon scale is equivalent to the scale on which polarization has been detected.
Furthermore, the polarized fraction of the temperature anisotropy must be small, normally one order of magnitude smaller than the anisotropy in the temperature. This is simply because these photons mush have passed through an optically thin plasma, otherwise they would not have reached us but they would have scattered and destroyed the sub-horizon (i.e., below 1°) correlation in the CMB, contrary to what we observe (see e.g., [190]).
The dependence Thomson scattering differential cross section on polarization is expressed as
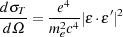 |
(5) |
where e and me are the electron charge and mass and є ⋅ є' is the angle between the incident and scattered photons. The right hand panel of Figure 7 shows how the Thomson scattering produces polarization of the CMB photons. If the CMB photons scatter later due to reionization and the incident radiation has a quadrupole moment, then it will be scattered in a polarized manner on the scale roughly equivalent to the horizon scale at the redshift of scattering. That is why the scale at which the large scale polarization is detected gives information about the reionization redshift.
The polarization field of the CMB photons is usually described in terms of the so called "electric" (E) and "magnetic" (B) components which can be derived from a scalar or vector field. The harmonics of an E-mode have (-1)ℓ parity on the sphere, whereas those of B-mode have (-1)ℓ+1 parity. Under parity transformation, i.e., n → - n, the E-mode thus remains unchanged for even ℓ , whereas the B-mode changes sign and vice versa. Fig. 8 illustrates such (a)symmetry under parity transformation for the simple case of ℓ = 2, m = 0 [86].
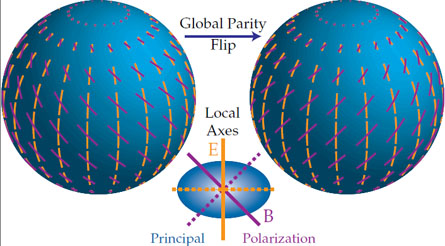 |
Figure 8. The E and B polarization modes are distinguished by their behavior under parity transformation. The local distinction is that the E mode is aligned with the principle axis of polarization whereas the B mode is 45° crossed with it (this figure is taken from Hu and White [86]). |
Various physical processes lead to different effects on the CMB polarization. Most of these effects are expected to produce E mode polarization patterns on the CMB. However, gravitational waves in the primordial signal and gravitational lensing of the CMB on its way to us produce a B mode polarization patterns. A large scale E mode polarization signal could only be caused by the process of reionization. The main reason for this is that large scale polarization could not be caused by causal effects on the last scattering surface which has a 1° scale whereas reionization, which occurs much later, has no such restriction. Figure 9 shows the measured and predicted CMB angular power and cross-power spectra from the WMAP 3rd year data. The existence of large scale correlation in the E-mode is a strong indication that the Universe became ionized around redshift z ≈ 10. The argument in essence is mostly geometric, namely it has to do with the scale of the E-mode power spectrum as well as the line of sight distance to the onset of the reionization front along a given direction. Some authors have also argued that one can have somewhat more detailed constraints on reionization from the exact shape of the CMB E-mode polarization large scale bump [84, 110, 138]. Unfortunately however, the large cosmic variance at large scales limits the amount of possible information one can extract. Still, the Planck surveyor is expected to be able to retrieve some of the large scale bump shape.
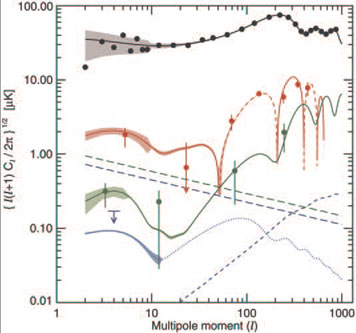 |
Figure 9. The temperature and E-mode polarization power and cross-power spectra as measure by the WMAP satellite [152]. Plots of signal for TT (black), TE (red ), and EE ( green) for the best-fit model. The dashed line for TE indicates areas of anticorrelation. For more details about this Figure we refer the reader to the Page et al. [152]. Notice the excess power on large scales caused by reionization seen in the TE and EE power spectra. |
From Figure 9 one can also deduce the optical
depth for Thomson scattering,
 , caused by the scattering
of the CMB photons off free electrons released by reionization to be
0.087 ± 0.017
[57].
This could be turned into a constraint on the global reionization
history through the integral,
, caused by the scattering
of the CMB photons off free electrons released by reionization to be
0.087 ± 0.017
[57].
This could be turned into a constraint on the global reionization
history through the integral,
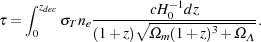 |
(6) |
Here zdec is the decoupling redshift,
 T is the
Thomson cross section, µ is the mean molecular
weight and ne is the electron density. This formula
works for the optical depth along each sight line but also for the mean
electron density, i.e., mean reionization history, of the Universe.
T is the
Thomson cross section, µ is the mean molecular
weight and ne is the electron density. This formula
works for the optical depth along each sight line but also for the mean
electron density, i.e., mean reionization history, of the Universe.
An important point to notice here is that, in order to turn
 into a
measurement of the reionization redshift, one needs a model for
ne as a function of redshift. Hence, one has to be
careful when using the reionization redshift given by CMB papers as in
most cases a gradual reionization is assumed. Sudden reionization gives
a one to one correspondence between the measured optical depth and the
reionization redshift, e.g., the WMAP measurement optical depth implied
zi = 11.0 ± 1.4.
into a
measurement of the reionization redshift, one needs a model for
ne as a function of redshift. Hence, one has to be
careful when using the reionization redshift given by CMB papers as in
most cases a gradual reionization is assumed. Sudden reionization gives
a one to one correspondence between the measured optical depth and the
reionization redshift, e.g., the WMAP measurement optical depth implied
zi = 11.0 ± 1.4.
However, sudden reionization is very unlikely and most models predict a more gradual evolution of the electron density as a function of redshift. Furthermore, in such scenarios the redshift of reionization is not clearly defined, therefore authors refer instead to the redshift at which half of the IGM volume is ionized, zxHI = 0.5. Obviously, in the case of sudden reionization the two redshifts coincide, zi = zxHI = 0.5. It is also important to notice that in the case of sudden reionization the WMAP measured Thomson optical depth does not imply that the redshift at which half the IGM is ionized is the same as zi and in most cases one obtains zxHI = 0.5 < zi [206].
The patchy nature of the reionization process will also leave an imprint at arcminute scales on the CMB sky. Such an imprint will be mostly caused by the reionization bubbles that form during the EoR. However, the strength of the reionization signal at small scales is found to be smaller than that caused by gravitation lensing and is very hard to extract unless the experiment has a very high signal-to-noise at such small scales [54].
2.3. The Intergalactic Medium at z
 6
6
There are a number
of other observations that put somewhat less certain constraints on
reionization. Those constraints come mostly from detailed analysis of
high resolution Lyman  forest data and from the observation of high redshift Lyman break
galaxies. Here we present the two "strongest" of those constraints.
forest data and from the observation of high redshift Lyman break
galaxies. Here we present the two "strongest" of those constraints.
2.3.1. IGM Temperature Evolution
Another constraint on the reionization history comes from studying the
thermal history of the IGM. Due to its low density, the intergalactic
medium cooling time is long and retains some memory of when and how it
was last heated, namely, reionized. Hence, measuring
the IGM temperature at a certain redshift
( 3.5) allows us
to reconstruct,
under certain assumptions, its thermal history up to the reionization
phase where the IGM has been substantially heated. Such a measurement
has been carried out by a number of authors using
high resolution Lyman
3.5) allows us
to reconstruct,
under certain assumptions, its thermal history up to the reionization
phase where the IGM has been substantially heated. Such a measurement
has been carried out by a number of authors using
high resolution Lyman  forest data, especially using the very low
column density absorption lines. The width of these
absorption features carries information about the temperature of the
underlying IGM. This temperature obviously varies with density and
with other parameters like the background UV flux. Based on both
theoretical arguments
[87]
and on numerical simulations
[201]
in the linear and quasilinear regime, the temperature-density relation
follows the simple power law,
forest data, especially using the very low
column density absorption lines. The width of these
absorption features carries information about the temperature of the
underlying IGM. This temperature obviously varies with density and
with other parameters like the background UV flux. Based on both
theoretical arguments
[87]
and on numerical simulations
[201]
in the linear and quasilinear regime, the temperature-density relation
follows the simple power law,
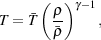 |
(7) |
where 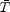 is the
temperature of the IGM at the mean density of the Universe and
is the
temperature of the IGM at the mean density of the Universe and
 is the
adiabatic power law index.
Figure 10 shows the so called phase diagram,
i.e., the relation between the temperature and density,
obtained from a cosmological hydrodynamical simulation
[161].
The relation between the density and temperature at the low density end
of the diagram, marked as diffuse background, follows a power law.
The hot phase at intermediate densities where cooling is not efficient,
is driven by shock heating. At high densities, cooling becomes very
efficient and drives the gas temperature. At high redshifts
more than 90% of the gas is in the diffuse phase.
is the
adiabatic power law index.
Figure 10 shows the so called phase diagram,
i.e., the relation between the temperature and density,
obtained from a cosmological hydrodynamical simulation
[161].
The relation between the density and temperature at the low density end
of the diagram, marked as diffuse background, follows a power law.
The hot phase at intermediate densities where cooling is not efficient,
is driven by shock heating. At high densities, cooling becomes very
efficient and drives the gas temperature. At high redshifts
more than 90% of the gas is in the diffuse phase.
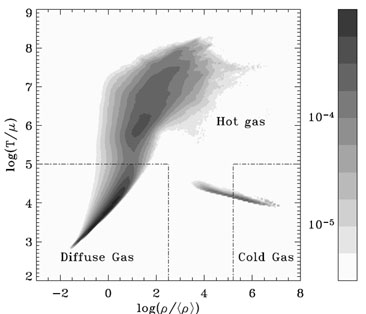 |
Figure 10. The different baryon phases in
the |
Given the validity of equation 7 at low densities, it is meaningful
to define an IGM temperature as the gas temperature at the mean density,
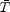 .
Such a measurement has been performed by a number of authors at z
≈ 3-4
[111,
178,
203,
225]
and recently at z ≈ 6 by
[17].
.
Such a measurement has been performed by a number of authors at z
≈ 3-4
[111,
178,
203,
225]
and recently at z ≈ 6 by
[17].
The usefulness of this temperature to
constrain the reionization history was first realized by
[202,
88]
who used the measured temperature around redshift 3 to set
z ≈ 9 as an upper limit for the reionization process. Bolton
et al.
([17])
have recently confirmed these findings with higher redshift quasars.
That is, the measured temperatures of the IGM at redshift z
≈ 3 and z ≈ 6
are too high for the bulk of reionization to have occurred at redshift
 10.
10.
After reionization, the evolution of the IGM mean temperature
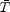 is given by
is given by
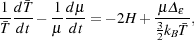 |
(8) |
where H is the Hubble parameter, kB is the
Boltzmann constant, µ is the mean molecular weight, and
 є
is the effective radiative cooling rate (in
units of ergs g-1 s-1).
є
is the effective radiative cooling rate (in
units of ergs g-1 s-1).
 є
is negative (positive) for net cooling (heating) and includes
photoelectric heating and cooling via recombination, excitation, inverse
Compton scattering, collisional ionization, and bremsstrahlung. Without
cooling/heating processes the cooling rate is set by adiabatic cooling,
namely, Hubble expansion. This equation enables us to calculate the
temperature evolution as a function of redshift. Measuring the IGM
temperature at a given redshift will allow us to extrapolate back in
time until we reach a temperature of 6 × 104 K which is the
temperature at which hydrogen ionizes. Figure 11
demonstrates this procedure
[202].
є
is negative (positive) for net cooling (heating) and includes
photoelectric heating and cooling via recombination, excitation, inverse
Compton scattering, collisional ionization, and bremsstrahlung. Without
cooling/heating processes the cooling rate is set by adiabatic cooling,
namely, Hubble expansion. This equation enables us to calculate the
temperature evolution as a function of redshift. Measuring the IGM
temperature at a given redshift will allow us to extrapolate back in
time until we reach a temperature of 6 × 104 K which is the
temperature at which hydrogen ionizes. Figure 11
demonstrates this procedure
[202].
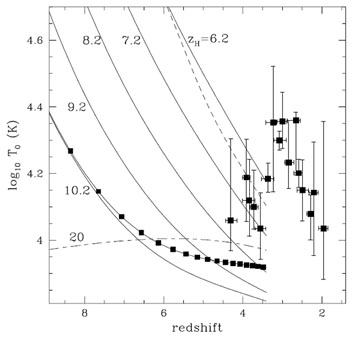 |
Figure 11. Temperature evolution of the IGM
above redshift 3.4. The solid curves indicate the evolution of the
temperature at the mean density for various H I
reionization redshifts zH, as
indicated. The temperature after hydrogen reionization is assumed to
be T0 = 6 × 104 K, and the hydrogen
photoionization rate is
|
Obviously, the weak point of this argument is the assumption that one knows the cooling/heating function of the IGM at every redshift up to the time of reionization. Still, this is a useful argument and certainly any model for the reionization history would have to explain the temperature we measure at lower redshifts.
2.3.2. Number of Ionizing Photons per Baryon
Another constraint that comes mostly from the Lyman
 forest but
also from the recently discovered galaxies at z
forest but
also from the recently discovered galaxies at z
 7 is the
number of ionizing photons per baryon. Using physically motivated
assumptions for the mean free path of ionizing photons, Bolton and
Haehnelt
([18])
turned the measurement of the photoionization rate into an
estimate of the ionizing emissivity. They showed that the inferred
ionizing emissivity in comoving units, is nearly constant over the
redshift range 2-6 and corresponds to 1.5-3 photons emitted per
hydrogen atom over a time interval corresponding to the age of the
Universe at z = 6. Completion of reionization at or before
z = 6 requires therefore, either an emissivity which rises
towards higher redshifts or one which remains constant but is dominated
by sources with a rather hard spectral index, e.g., mini-quasars.
7 is the
number of ionizing photons per baryon. Using physically motivated
assumptions for the mean free path of ionizing photons, Bolton and
Haehnelt
([18])
turned the measurement of the photoionization rate into an
estimate of the ionizing emissivity. They showed that the inferred
ionizing emissivity in comoving units, is nearly constant over the
redshift range 2-6 and corresponds to 1.5-3 photons emitted per
hydrogen atom over a time interval corresponding to the age of the
Universe at z = 6. Completion of reionization at or before
z = 6 requires therefore, either an emissivity which rises
towards higher redshifts or one which remains constant but is dominated
by sources with a rather hard spectral index, e.g., mini-quasars.
With the installation of the WFC3 camera aboard the Hubble Space Telescope, searches for high redshift galaxies at z = 6-10 have improved dramatically. In particular, a number of authors [145, 23, 33, 125] have reported detection of very high redshifts galaxies using the Lyman-break drop-out technique. The most striking result of these studies is the low number of galaxies found beyond redshift ≈ 6, making it very hard for these galaxies to ionize the Universe. This conclusion depends however on assuming a luminosity function for galaxies at these redshifts, a function that is very poorly known. More surprising is the very steep drop in the number of galaxies at redshift z ≈ 9 [22] which makes it even harder to explain reionization with such galaxies.
The last two observational findings have led some authors to claim that the reionization is photon starved, i.e., has a low number of ionizing photons per baryon, which results in a very slow and extended reionization process [18, 34]. Figure 12 shows the number density of ionizing photons (left-hand vertical axis) and number of ionizing photons per baryon (right-hand vertical axis) as a function of redshift. The number of ionizing photons per baryon at redshift 6 is of the order of 2. More recent results deduced from Lyman-break galaxies are consistent with this figure and show an even lower ratio of ionizing photons per baryon at higher redshifts.
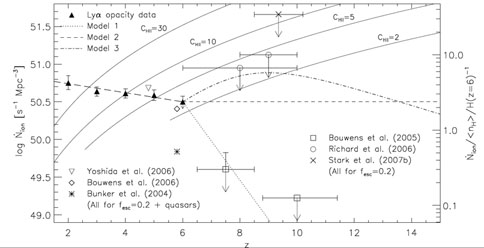 |
Figure 12. Observational constraints on the
emission rate of ionizing photons per comoving Mpc,
|
2.4. Other Observational Probes
In addition to the probes that we discussed so far, there are a
large number of other observational probes that could potentially add
valuable input to the reionization models. Examples of such
probes are cosmic infrared and soft x-ray backgrounds
[52],
Lyman  emitters
[149],
high redshift QSOs
[137]
and GRBs
[31],
metal abundance at high redshift
[172],
etc. However, such probes currently provide very limited constraints
on the EoR.
emitters
[149],
high redshift QSOs
[137]
and GRBs
[31],
metal abundance at high redshift
[172],
etc. However, such probes currently provide very limited constraints
on the EoR.
In the coming chapters we will focus on the very large effort currently
made to measure the diffuse neutral hydrogen in the IGM as a function
of redshift up to z
 11 using the
redshifted 21 cm emission line. This probe will give the most
direct and detailed evidence on the reionization process.
11 using the
redshifted 21 cm emission line. This probe will give the most
direct and detailed evidence on the reionization process.
1 Notice that this is a different "visibility" than the one used in radio interferometry which we discuss in section 5. Back.