4. RESULTS FROM CURRENT MODELS: INSIGHTS AND PUZZLES

We return for a moment to Fig. 1 and 2 to illustrate some general insights into the process of galaxy formation and evolution in the ΛCDM framework that have arisen from numerical simulations. Starting with the left column of Fig. 1, we see that structure formation in the dark matter component proceeds via the formation of sheets or giant walls, which form filaments where they intersect. Dark matter halos form at the intersection of filaments, which funnel dark matter and gas into halos like tributaries flowing into a lake. Comparing the first and second columns of Fig.1, one can see that there is a very strong correspondence between the dark matter and gas density fields on large scales. This illustrates that gas flows on large scales are dominated by gravity. Moving to the third column of Fig. 1, we can see that the gas surrounding massive halos is hot, and larger regions become heated as time progresses. This heating is in part due to shock heating as halos collapse, but in these simulations is in large part due to star formation and AGN feedback. Finally, examining the rightmost column of Fig. 1, we see that metals are dispersed to quite large distances from galaxies, and polluted regions again fill a larger comoving volume over time. Fig. 2 shows how filaments of relatively cold gas can sometimes penetrate some distance into hot halos – these supply the “cold mode” accretion discussed earlier (sometimes called “stream fed” accretion). The inset in Fig. 2 emphasizes how small galaxies are compared with the structures seen in the “cosmic web”.

4.1. Global Properties

4.1.1. Stellar Mass Assembly Over Cosmic Time. A fundamental observational target for modelers is reproducing the statistical distributions of global properties for galaxy populations at different cosmic epochs, such as luminosity functions (LF), stellar mass functions, and cold gas mass functions. It has been realized for some time that the observed local LF or SMF is not ‘naturally’ reproduced by galaxy formation models based within the ΛCDM paradigm: CDM models generically predict that the slope of the mass function of dark matter halos has a slope of α_h ∼ −2, while the slope of the observed galaxy SMF locally is much shallower (α_g ≃ −1.3). A number of authors suggested that supernova feedback could flatten out the low-mass slope by suppressing star formation in low-mass halos (Larson 1974, Dekel & Silk 1986, White & Frenk 1991). Furthermore, although ΛCDM predicts an exponential cut-off or “knee” in the halo mass function, with a similar functional form to that of the observed SMF, the halo mass function turn-over is at much larger masses. Although the cooling times in these massive, group and cluster-sized halos are predicted to be somewhat longer than in low-mass halos (Rees & Ostriker 1977, Blumenthal et al. 1984), this turns out to be insufficient to explain the very inefficient star formation required to reconcile the abundance of massive galaxies with that of dark matter halos.

After decades of effort, theoretical models of galaxy formation are now fairly successful at reproducing the SMF of galaxies at z ∼ 0 by invoking a plausible, if still in most cases schematic, set of physical processes. Fig. 4 shows a compilation of predictions of recent numerical hydrodynamic simulations and semi-analytic models for the SMF from z = 4 to z ∼ 0. These models are all taken directly from the original publications and no attempt has been made to calibrate them to the same set of observations or to correct for the slight differences in cosmology ⁴. This success has been obtained by “tuning” not only free parameters but also the recipes associated with the sub-grid physics (star formation, stellar feedback, AGN feedback). Predictions of the build-up of stellar mass over cosmic time, with these recipes and parameters held fixed, present a more stringent test of the models.

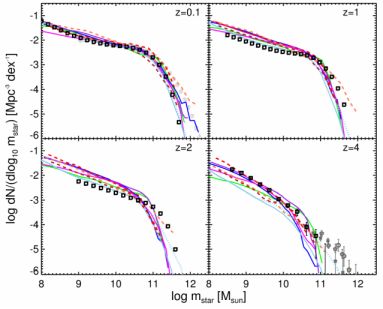Figure 4. Galaxy stellar mass function at redshifts z ∼ 0–4. In the z = 0.1, z = 1, and z = 2 panels, black square symbols show a double-Schechter fit to a compilation of observational estimates. Observations included in the fit are: z = 0.1 – Baldry et al. (2008), Moustakas et al. (2013); z = 1 and z = 2 panels – Tomczak et al. (2014), Muzzin et al. (2013). The fits shown at z = 1 and z = 2 are interpolated to these redshifts from adjacent redshift bins in the original published results. The formal quoted 1σ errors on the estimates shown in these three panels are comparable to the symbol size, and are not shown for clarity (the actual uncertainties are much larger, but are difficult to estimate accurately). In the z = 0.1 panel, the estimates of Bernardi et al. (2013) are also shown (open gray circles). In the z = 4 panel we show estimates from Duncan et al. (2014, squares), Caputi et al. (2011, crosses), Marchesini et al. (2010, circles, for z = 3–4), and Muzzin et al. (2013, pentagons, z = 3–4). Solid colored lines show predictions from semi-analytic models: SAGE (Croton et al. in prep, dark blue), Y. Lu SAM (Lu et al. 2013, magenta), GALFORM (Gonzalez-Perez et al. 2014, green), the Santa Cruz SAM (Porter et al. 2014, purple), and the MPA Millennium SAM (Henriques et al. 2013). The dotted light blue line shows the Henriques et al. (2013) SAM with observational errors convolved (see text). Colored dashed lines show predictions from numerical hydrodynamic simulations: EAGLE simulations (Schaye et al. 2014, dark red), ezw simulations of Davé and collaborators (Davé et al. 2013, bright red) and the Illustris simulations (Vogelsberger et al. 2014b, orange).

In a broad brush sense the model predictions are generally encouraging. A very general prediction of ΛCDM-based models is that galaxies built up their stellar mass gradually over time, which is supported by observations. All models predict efficient early star formation (z ≳ 4) in low mass halos, and steep stellar mass and rest-UV luminosity functions at these early epochs, in agreement with observations. Models including AGN feedback or heuristic quenching predict that massive galaxies formed earlier and more rapidly than lower mass galaxies, again in qualitative agreement with observations. Most models even demonstrate very good quantitative agreement, within the errors on stellar mass estimates, between predicted and observed SMF and LF for massive galaxies (m_star > M_char). Note that in Fig. 4, most of the theoretical predictions for the stellar masses have not been convolved with the expected uncertainties that are inherent in the observational estimates. Including these in a simplified manner brings the model predictions into better apparent agreement with the observations on the massive end (e.g. Lu et al. 2013, Henriques et al. 2013), as shown here for the MPA SAM as an illustration. For a more detailed study of this issue see Mitchell et al. (2013).

As can be seen as well in Fig. 4, models currently have greater difficulties reproducing the abundances and assembly histories of low-mass galaxies at intermediate redshifts. Fontanot et al. (2009) demonstrated that three independently developed SAMs overproduce galaxies with m_star ≲ 10¹⁰ M_⊙ by a factor of ∼ 2–3 over the redshift range 4 ≲ z ≲ 0.5. Weinmann et al. (2012) showed that a qualitatively similar problem exists for SAMs and for hydrodynamic simulations. This problem appears to persist even in the latest state-of-the-art cosmological hydrodynamic simulations, as seen in Fig. 4, and already pointed out in the case of Illustris by Torrey et al. (2014). As discussed in Fontanot et al. (2009), several different sets of observations suggest that massive galaxies form early and rapidly, while low-mass galaxies form later and with a more extended timescale — the phenomenon that is often referred to as “downsizing” or “staged” galaxy formation (Noeske et al. 2007). The overproduction of low-mass galaxies is a symptom of the failure of current models to reproduce this mass-dependence in the star formation histories of galaxies. Low-mass dark matter halos actually have earlier formation times than high-mass halos — the opposite of the trend seen in observations (Conroy & Wechsler 2009). In current simulations, the star formation histories closely trace the DM mass accretion histories, thus similarly failing to reproduce the observed trend.

It seems clear that the sub-grid recipes controlling star formation and/or stellar feedback need to be modified in order to solve this problem. Henriques et al. (2013) found that making the stellar feedback stronger and modifying the timescale for the re-accretion of ejected gas led to significant improvement in the MPA-SAM for the predicted abundances of low-mass galaxies as well as other observed properties at z ≲ 3. White et al. (2014) investigated several classes of empirical solutions to this problem, including modifying the efficiency of stellar driven galaxy outflows, modifying the timescale for gas to turn into stars, and modifying the timescale for gas to be accreted (or re-accreted) into galaxies. They concluded that solutions that modified the outflow efficiencies and accretion timescales were the most promising. Moreover, Torrey et al. (2014) experimented with changing the coupling strength and velocity of the stellar driven winds, and found that this can change the normalization of the SMF at the low-mass end, but cannot change the evolutionary shape, which is what is required to solve this problem.

A convenient way to assess the success of a cosmological simulation in reproducing the galaxy SMF or LF is via empirical constraints on the relationship between stellar mass (or luminosity) and halo mass, as derived by “galaxy-halo mapping” techniques such as SHAM and HOD, and other methods such as galaxy-galaxy lensing, clustering, satellite kinematics, and X-ray observations (Moster et al. 2010b, Behroozi et al. 2010, Moster et al. 2013, Behroozi et al. 2013a and references therein). Different methods and groups are generally all in broad agreement that star formation feedback plays a crucial role in shaping this relationship for halos with M_h ≲ 10¹² M_⊙, with photo-ionization squelching perhaps also playing a significant role below halo masses of about a few 10¹⁰ M_⊙ (this mass scale remains uncertain; see Section 3.3.1). At larger halo masses, M_h ≳ 10¹² M_⊙, there is a general consensus that AGN feedback probably plays an important role, although other processes (such as gravitational heating) may contribute as well (Khochfar & Ostriker 2008, Johansson et al. 2009b, Birnboim & Dekel 2011). In order to reproduce the slope of the stellar mass-halo mass (m_star − M_halo) relation at low masses, most models adopt stellar feedback recipes that either assume or result in mass loading factors that increase fairly strongly with decreasing halo mass or circular velocity, similar to the energy- or momentum-driven wind scalings discussed in Section 3.3.2.

There is a broad though not universal consensus that AGN feedback implemented purely via deposition of thermal energy associated with the radiatively efficient mode of BH growth (as in e.g. Di Matteo et al. 2005) does not by itself suppress cooling and star formation in massive halos enough (or on long enough timescales) to satisfy observational constraints. Although thermal energy deposition can temporarily slow or halt cooling, after several Gyr, the gas starts to re-cool and form stars (Gabor & Davé 2012, Choi et al. 2014b). An exception is the stochastic thermal feedback model implemented in EAGLE, which reproduces the observed stellar fractions very well, though there is still tension between the predicted temperatures of the hot gas in group- and cluster-sized halos and X-ray observations (Schaye et al. 2014). Another solution on the high-mass end is nearly constant injection of energy via “jet mode” feedback, although as discussed in Section 3.3.3, implementations of this process in cosmological simulations remain schematic. Inclusion of the momentum deposition associated with the radiatively efficient mode also appears to be able to suppress cooling for longer (Choi et al. 2014b).

4.1.2. Global Scaling Relations: Gas, Star formation and Metals. Galaxies are comprised of stars, gas, metals, black holes, and dark matter. The scaling relations between these properties as a function of mass and redshift provide crucial constraints on galaxy growth, and are in principle among the most direct ways to constrain baryon cycling processes.

The basic origin of many scaling relations can be understood in a simple framework based on mass balance in the ISM (alternately called an “equilibrium”, “bathtub”, or “gas regulator” model):

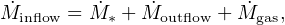(6)

where the terms are the baryonic mass inflow rate, SFR, mass outflow rate, and rate of change of the mass in the gas reservoir. When averaged over cosmological timescales, _gas is expected to be small compared to the other terms (Finlator & Davé 2008, Davé et al. 2012, Dekel & Mandelker 2014), though its evolution can have important effects (Lilly et al. 2013). Inflow into halos is driven primarily by gravitational accretion from the IGM (Kereš et al. 2005, Dekel et al. 2009). The rate at which dark matter halos grow, the halo mass accretion rate (_halo), is well-characterized in ΛCDM, and roughly given by _halo ∝ M_halo(1 + z)^2.5 (Dekel et al. 2009, Faucher-Giguère et al. 2011). However, preventive feedback within galaxy halos can retard gas accretion into the ISM, and outflows can remove fuel for star formation even after it enters the ISM, so _inflow may not trace _halo.

We can rewrite equation 6 as

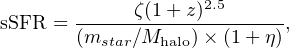(7)

where ζ is the fraction of material entering the virial radius that makes it into the ISM, and η≡ _outflow / _star is the outflow mass loading factor. The dependence of sSFR on m_star and z therefore reflects the evolving combination of accretion and feedback.

Figure 5 shows a comparison of SFR vs. m_star for the SAMs and simulations shown in Figure 4, along with a compilation of recent observational determinations as described in the figure caption. All models generally reproduce the near-unity slope, at all redshifts. Most models match the amplitude at z ∼ 0, although the turnover at high masses due to quenching can vary significantly (and can be sensitive to the definition of “star forming” galaxies), and models tend to predict a steeper trend at low masses. By z ∼ 1−2, it is clear that most models fall below the observations, a long-standing discrepancy first highlighted in (Daddi et al. 2007). The redshift dependence of the sSFR is generically difficult to match in models because it differs strongly in the intermediate redshift regime (4 ≲ z ≲ 0.5) from the dependence predicted by _halo (Davé 2008, Sparre et al. 2014). By z = 4, some models are able to match the data, though others continue to fall substantially short. The normalization of the predicted SFR vs. m_star relation depends on resolution and the calibration of the sub-grid parameters — e.g. Schaye et al. (2014) show (their Fig. 11) that a higher resolution simulation in the EAGLE suite, re-calibrated to the SMF, predicts a higher SFR at m_star ≲ 10¹⁰, in better agreement with the observations. However, the redshift dependence of the sSFR is roughly unchanged (Furlong et al. 2014).

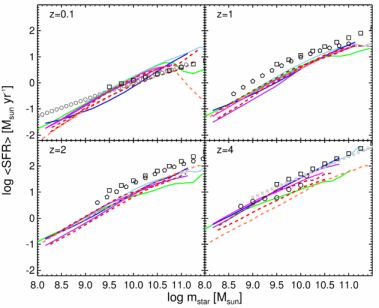Figure 5. The average star formation rate in bins of stellar mass, for redshift bins from z = 0–4. Grey and black symbols show observational estimates: z = 0.1 – Salim et al. (2007, open circles); z = 1 and z = 2 – Whitaker et al. (2014, pentagons, interpolated in redshift from the published results); z = 4– Steinhardt et al. (2014, crosses); Salmon et al. (2014, circles); all panels – fit to data compilation from Speagle et al. (2014, squares). Colored lines show predictions from semi-analytic models and numerical hydrodynamic simulations; key is the same as in Fig. 4. Note that the observational estimates shown are for star forming galaxies; different methods have been used to isolate the “star forming sequence” from “quiescent” galaxies. Some of the modelers have applied a cut to select star forming galaxies, but some have not.

These trends can be generally understood in the mass balance framework. From abundance matching, the m_star − M_halo relation is constrained to evolve mildly with redshift (Behroozi et al. 2013a, Moster et al. 2013). If ζ and η also evolve slowly, then sSFR should evolve as ∼ (1 + z)^2.5. This is indeed roughly the evolution observed out to z ∼ 2 (e.g. Lilly et al. 2013, Speagle et al. 2014, Whitaker et al. 2014). However, to higher redshift the evolution slows, suggesting that either the m_star − M_halo relation or η is higher, or that ζ is lower. The assumption of _gas ≈ 0 may be faulty at very early epochs if the inflowing gas cannot be processed in the ISM fast enough, which observations suggest may be the case at z ≳ 4 (Papovich et al. 2011). It had been suggested that the efficiency of converting ISM gas into stars is reduced owing to the lower metallicity at early epochs which results in less efficient formation of molecular gas (Krumholz & Dekel 2012), but hydrodynamic simulations and SAMs incorporating H₂ formation modeling suggest that this effect is not large enough to solve the problem at the observed mass scales (Christensen et al. 2012, Somerville et al. 2014). Moreover, the EAGLE simulations also include a metallicity-dependent density threshold for star formation as proposed in Schaye (2004), representing the same physical effect, but still suffer the same problem. Hence although it is encouraging that most models are now able to predict the sSFR evolution to within a factor of 2–3 and predict roughly the right qualitative trend, such discrepancies, if real, could be pointing to a need to revise our basic understanding of the physical processes regulating star formation at these epochs.

The mass dependence of the sSFR also poses interesting challenges to models. In detail, the halo mass accretion rate has a super-linear dependence on M_halo, which would naively translate into a positive slope for sSFR(m_star). Observations indicate a sub-unity slope, becoming shallower with time (see Figure 5). Part of this may be due to the fact that for M_halo ≳ 10¹¹ M_⊙, an increasing amount of halo inflow is gravitationally shocked into hydrostatic equilibrium (Birnboim & Dekel 2003, Kereš et al. 2005, Gabor & Davé 2012). Simulations show this is sufficient to explain the mildly negative slope in moderate-sized halos (Faucher-Giguère et al. 2011, Davé et al. 2011b), but is insufficient to explain the rapid increase in quenched galaxies at high masses, which requires additional feedback, likely associated with AGN.

Moreover, models with outflows tuned to reproduce the observed SMF (hence m_star − M_halo) predict a flat or positive slope for sSFR(m_star) at M_halo ≲ 10¹¹M_⊙, while observations show a negative slope. The stochasticity of star formation in dwarf galaxies (Tolstoy et al. 2009) may result in a duty cycle whereby observed samples preferentially select dwarfs that are in a high sSFR state, but observations show that essentially all isolated dwarfs in the nearby universe are star-forming (Geha et al. 2012). This is an aspect of the “dwarf galaxy conundrum” highlighted in Weinmann et al. (2012) and White et al. (2014) and discussed above, which remains a puzzle: in current models that are normalized to fit the present-day SMF, dwarf galaxies not only form their stars too early (resulting in the low-mass excess at intermediate redshift seen in Fig. 4), they also have sSFR that are well below the observed values (see also Torrey et al. 2014). At higher redshifts, the mass dependence is in good agreement with existing observations, but deeper near-IR data is needed to test if a similar discrepancy occurs in mass-selected samples of dwarfs at z ≳ 1.

Another key scaling relation is the stellar mass-gas phase metallicity relation (MZR), which can also be understood from equation 6. Given a metal yield y per unit star formation, the metallicity will be the yield times the SFR, divided by the amount of accreting gas, i.e.

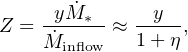(8)

where this approximation is valid in the limit of no recycled (i.e. previously enriched) accretion into the ISM (Finlator & Davé 2008). Wind recycling is generally more rapid in more massive galaxies (Oppenheimer et al. 2010), which will tend to make the MZR steeper. Also, outflows that are significantly more enriched than the ISM can result in a lower metallicity. Hence the MZR primarily reflects galactic outflows, modulated by wind recycling and the “metal loading factor” (Peeples & Shankar 2011).

Figure 6 shows the predicted MZR in our suite of SAMs and simulations, compared with observations. We emphasize that, due to uncertainties in the theoretical yields of at least a factor of ∼ 2, and differences of ∼ 30 percent in the adopted value of solar metallicity in different simulations, the absolute normalizations of the predicted MZR should not be given as much weight as the trends with mass and redshift. We also show a recent compilation of observational estimates. Gas-phase abundance measures are sensitive to calibration (Kewley & Ellison 2008), but it is usually the case that relative abundances are more consistent among various indices. Hence the slope of the observed MZR is more robustly known than the amplitude, though the amplitude should still be accurate to within a factor of 2−3. We show MZR determinations at z ∼ 0.1, z ∼ 1, and z ∼ 2 converted to the same calibration, from (Zahid et al. 2013). We also show the local MZR from (Peeples et al. 2014), which uses the average of all of the calibrations presented in Kewley & Ellison (2008), and the local “direct method” MZR from Andrews & Martini (2013).

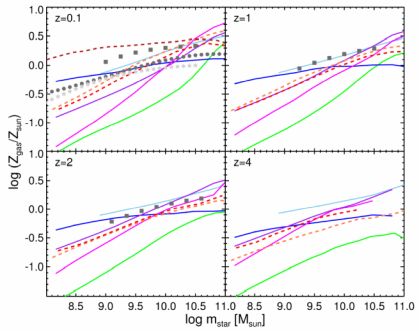Figure 6. The average metallicity of cold gas in bins of stellar mass, for redshift bins from z = 0–4. Grey and black symbols show observational estimates: z = 0.1 – Peeples et al. (2014, filled circles); Andrews & Martini (2013, stars). In all panels, the filled squares show the compilation of Zahid et al. (2013). Colored lines show predictions from semi-analytic models and numerical hydrodynamic simulations; key is the same as in Fig. 4.

To explore the origin of the slope discrepancy, note that equation 8 shows that (in the absence of recycling and metal-enriched outflows), when η≫ 1 as is generally the case at low masses in these models, the observed MZR Z ∝ m_∗^0.3 (Tremonti et al. 2004) implies η ∝ m_∗^−0.3. When such a scaling (which is similar to the momentum driven wind scaling) is implemented into hydrodynamic simulations, this produces good agreement with the observed MZR (Finlator & Davé 2008, Davé et al. 2011a), but the predicted SMF is somewhat too steep at the faint end (Davé et al. 2011b). Ameliorating this by incorporating a steeper mass dependence of η results in an MZR that is too steep (Davé et al. 2013). Accounting for wind recycling does not help this problem– Oppenheimer et al. (2010) highlighted the importance of wind recycling in shaping the SMF at intermediate masses, but in general wind recycling is more important at higher masses, which further steepens the MZR. In general, current simulations have difficulty simultaneously matching the low-mass ends of the SMF and the MZR, suggesting that enrichment in low-mass galaxies is not fully understood. This problem was also discussed in the context of the Illustris simulations by Torrey et al. (2014), who speculated that this tension may suggest that preventative, rather than ejective, feedback is dominant in low-mass galaxies.

Cold gas scaling relations provide information on the fuel for star formation. CO measurements are currently the best tracer of molecular gas content, although there remain significant uncertainties in the conversion factor from CO to H₂ (X_CO; Bolatto et al. 2013), particularly to higher redshifts. Observations show that low-mass galaxies are more gas-rich, with f_gas∝ m_∗^−0.57 (Peeples & Shankar 2011). Direct estimates of the H₂ fraction of galaxies to high redshift from CO and dust-based methods (corrected for selection effects) indicate a rise in m_H2 / (m_H2 + m_star) back in cosmic time to z ∼ 2, then a plateau or possibly a slight decline (Geach et al. 2011, Tacconi et al. 2013, Saintonge et al. 2013, Scoville et al. 2014, Genzel et al. 2014). Empirical estimates of H₂ and total gas fraction based on extended SHAM modeling (Popping et al. 2014a) indicate a similar behavior.

Figure 7 shows a comparison of the cold gas fractions (≡ m_cold / m_star) in models, where we defined cold gas in the numerical simulations as that having a hydrogen number density n_h > 0.13 cm⁻³. At z = 0, models generally reproduce the steeply rising gas fractions to low masses, though some have gas fractions significantly below the observed ones at the lowest masses. Gas fractions tend to be fairly sensitive to the prescription used to turn that gas into stars, which varies significantly between models. This generic trend of gas fraction with galaxy mass in the models arises from two physical effects that make the global SFE lower in low-mass galaxies: stronger stellar feedback (Brooks et al. 2007), and less efficient formation of H₂ (Christensen et al. 2012, Popping et al. 2014b). Models generally predict rising gas fractions at a given mass to earlier epochs, in broad agreement with observational and SHAM-based estimates out to z ∼ 2, though gas fractions from the a priori models tend to be lower than the empirical SHAM predictions at z ∼ 2–1; perhaps this is another manifestation of the “dwarf galaxy conundrum” discussed above. Models that track H₂ formation generally predict that galaxies become increasingly H₂-dominated at higher masses and at high redshift (Popping et al. 2014b, Lagos et al. 2011a, Fu et al. 2010).

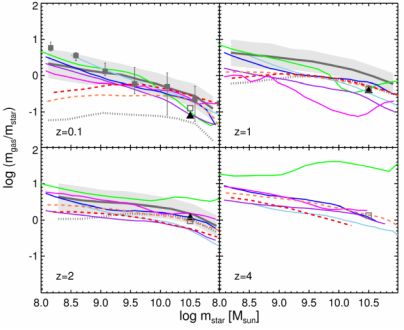Figure 7. The average cold gas fraction in bins of stellar mass, for redshift bins from z = 0–4. Grey and black lines and symbols show observational estimates: z = 0.1 – binned results from the compilation of Peeples et al. (2014, filled squares). In all panels, the open squares show the predictions of the “equilibrium model” presented in Saintonge et al. (2013), which are in good agreement with their data compilation and with the estimates of Genzel et al. (2014, (shown as solid triangles), extending up to z ∼ 3. The solid gray lines and light gray shaded areas show the empirical total cold gas fraction ((MHI + MH2) / mstar) estimates from Popping et al. (2014a). Dotted gray lines show the molecular fraction estimates (MH2 / mstar) from Popping et al. (2014a). Note that the z = 0 observational estimates shown are for H i + H2, while the z > 0 estimates are based on CO and most closely trace H2. Colored lines show predictions for the total cold gas fraction from semi-analytic models and numerical hydrodynamic simulations; color key is the same as in Fig. 4.

Atomic hydrogen (H i) can be detected in emission in nearby galaxies, and in distant galaxies via absorption. Since H i represents a transient phase of accretion from the ioinized IGM to the molecular ISM, it is necessary to include both self-shielding and molecular gas formation physics in order to model it, neither of which are straightforward at typical cosmological, or even zoom, resolutions. Nonetheless, SAMs and simulations can broadly reproduce H i mass functions and scaling relations (Popping et al. 2009, Obreschkow et al. 2009, Lagos et al. 2011a, Duffy et al. 2012, Davé et al. 2013, Popping et al. 2014b). H i may be a particularly good tracer of environmental processes including satellite quenching (Lagos et al. 2014, Rafieferantsoa et al. 2014), because it is usually arises in the more loosely-bound outskirts. In addition, SAMs and numerical simulations are being used to study the nature of H i seen in absorption (Lyman-limit and Damped Lyman-α systems), and its connection with galaxies identified in emission (Berry et al. 2014, Rahmati et al. 2013, Rahmati & Schaye 2014, Bird et al. 2014). These studies provide important complementary constraints on disk formation and feedback processes.

So far, we have only considered mean scaling relations, which can be understood in terms of the average accretion rate into the ISM. In the accretion-driven scenario, galaxies fluctuate around the scaling relations, and the timescale to return to the mean is comparable to that required to double the mass of the galaxy. Hence the scatter of the scaling relations reflects the frequency and efficacy of “perturbing” events. In particular, mergers can drive significant departures from the mean scalings. For example, galaxies that lie significantly above the SF main sequence are observed to have concentrated, spheroid-like (high Sersic) light profiles (Wuyts et al. 2011), as expected if they are driven by major mergers. Reproducing the scatter in the observed scaling relations over cosmic time is a stringent challenge that models are only beginning to tackle (e.g. Sparre et al. 2014).

For the mass-metallicity relation, the scatter is seen to be well-correlated with SFR, in the sense that galaxies at a given mass with low metallicity have high SFR (Mannucci et al. 2010, Lara-López et al. 2010) and high H i content (Lara-López et al. 2013, Bothwell et al. 2013a). This is a natural outcome of the accretion rate fluctuation scenario, since a galaxy that undergoes an uptick in accretion will increase its SFR and gas content, owing to a larger gas supply, and lower its metallicity since the accreted gas (or infalling galaxy) will tend to have lower metallicity (Davé et al. 2011a). This so-called “fundamental metallicity relation” has two aspects, namely this second-parameter trend, and the claim by Mannucci et al. (2010) that it is invariant with redshift from z ∼ 0−2.5. However, calibration uncertainties in metallicity measures owing to evolving ISM conditions (Kewley et al. 2013) make the redshift independence difficult to robustly confirm, and even the existence of this second-parameter trend with SFR is not as clear at higher redshifts (Steidel et al. 2014, Sanders et al. 2014).

4.1.3. Demographics of Star-Forming and Quiescent Galaxies. The existence of quiescent galaxies, that almost entirely ceased forming stars many billions of years ago, is an additional indication of the need for some sort of “quenching” mechanism — processes that prevent gas from cooling and/or forming stars. Peng et al. (2010) coined the terms “mass” and “environmental” quenching. In view of the strong correlations between quiescence and other galaxy internal properties (see Section 1.1), we prefer the terms “internal” and “environmental” quenching. Some of the discussion here will mirror that in Section 4.1.1, however, the requirements for producing the correct internal and environmental statistical correlations for quiescent galaxies are more stringent than simply reproducing the stellar mass function – models that reproduce the latter are not guaranteed to reproduce the former.

The massive galaxies that are predominantly early type and quiescent in the observed universe are expected to reside within massive dark matter halos (≳ 10¹² M_⊙). These halos are expected theoretically, and known observationally through X-ray observations, to be filled with hot gas at virial temperatures of a few × 10⁶ – 10⁸ K that is gravitationally shock-heated on infall, and enriched to about a third of solar. Assuming hydrostatic equilibrium, this gas should be cooling fairly rapidly, at rates of hundreds to thousands of solar masses per year. The absence of the signatures of gas cooling below about one-third of the virial temperature in clusters, along with the absence of large amounts of cold gas or young stars, constitutes the classical “cooling flow” problem (McNamara & Nulsen 2007) and references therein). This problem has its counterpart in theoretical models, in that it has proven difficult to find plausible physical mechanisms that can suppress cooling and keep galaxies in massive halos as quiescent as they are observed to be.

Simulations without any sort of “quenching” mechanism (such as AGN feedback) produce inverted color-magnitude relations (more massive and luminous galaxies are more likely to be blue and star forming) without any hint of bimodality (Somerville et al. 2008, Gabor et al. 2011). The first generation of SAMs that included AGN feedback were able to qualitatively reproduce the observed bimodality of the color and sSFR distribution and the fraction of quiescent galaxies as a function of stellar mass (Croton et al. 2006, Bower et al. 2006, Somerville et al. 2008, Kimm et al. 2009); certainly, including AGN feedback greatly improved the results relative to the old models. In these models, the mechanism that was primarily or entirely responsible for quenching was the “jet mode” type of feedback described in Section 3.3.3, in which star formation dies out because the hot gas halo is continually heated so the supply of new cold gas is cut off. More heuristic models, in which cooling is simply shut off when the dark matter halo exceeded a certain critical mass, performed nearly as well as models that explicitly implemented “jet mode” AGN feedback (Cattaneo et al. 2006, Kimm et al. 2009). Some recent SAMs reproduce the observed tighter correlation of the quiescent fraction with B/T than with stellar mass, while others do not, suggesting that this could provide constraints on quenching mechanisms (Lang et al. 2014).

Springel et al. (2005a) showed that including thermal AGN feedback in hydrodynamic simulations of isolated binary mergers was able to drive powerful winds that evacuated most of the cold gas from the galaxy, leading to strong quenching of star formation. These results motivated semi-empirical models positing that quenching associated with mergers, rapid black hole growth, and “radiative mode” AGN feedback could explain the growth of the quiescent early type population (Hopkins et al. 2008b, Hopkins et al. 2008a). However, subsequent work with semi-analytic models and cosmologically-based hydro simulations suggested that thermal feedback associated with the “radiative mode” of BH accretion, when implemented using algorithms similar to those of Springel et al. (2005b), is not able to produce long-lived quiescent galaxies, since it fails to prevent subsequent accretion which reactivates star formation within a Gyr or two (see e.g. Gabor et al. 2011, Choi et al. 2014b).

Following the approach presented in Sijacki et al. (2007), the Illustris simulations explicitly included both local thermal heating associated with black hole accretion above a critical rate (representing “radiative mode”), and more distributed heating associated with low BH accretion rates (representing “jet mode”). They produced a bimodal color magnitude diagram, with a red galaxy fraction as a function of stellar mass and environment in good agreement with observations by Peng et al. (2010) and others (Vogelsberger et al. 2014a). The observed red sequence colors have proven difficult to reproduce quantitatively in all types of models (Guo et al. 2011, Gabor & Davé 2012, Vogelsberger et al. 2014a), but significant uncertainties remain in this regime in the stellar population models that are used to predict such colors from models. In contrast, the “stochastic thermal” AGN feedback model as implemented in EAGLE does not explicitly have two distinct modes, and can still reproduce quenched galaxy observations at a similar level (Schaye et al. 2014). Cosmological zoom-in simulations including fast momentum-driven AGN winds also appear to be able to quench and maintain quiescence over long timescales without any explicit “jet mode” type feedback (Choi et al.C 2014b, Choi et al. in prep). Conversely, Gabor & Davé (2014) suggested that the presence of a hot halo kept hot by AGN feedback is sufficient to quench a galaxy, without the need for additional radiative mode feedback, showing that this reproduces both internal and environmental quenching as observed. Hence there remains much debate over the relative importance of these two AGN feedback modes, whether one or both are required, and even whether they are distinct.

Reproducing the observed patterns of “environmental quenching” has provided another challenge to models. Peng et al. (2012) showed that when SDSS galaxies were identified as “satellites” or “centrals” using a group catalog, the fraction of quiescent centrals depended only on stellar mass, while the fraction of quiescent satellites depended on both mass and environment. Certainly there are many candidate processes that could preferentially quench satellites, such as harrassment, tidal stripping, or ram pressure stripping. In many SAMs, galaxies are not allowed to accrete any new gas from the hot halo or the IGM once they become satellites (sometimes called “strangulation”). This is known to produce far too high a fraction of quiescent satellites (Weinmann et al. 2006b, Font et al. 2008, Kimm et al. 2009). Instead, satellite quenching seems to take a surprisingly long time, perhaps many Gyr (Wetzel et al. 2012). Hydrodynamic simulations indeed show that infalling satellites remain star-forming for at least a Gyr (Simha et al. 2009), as it takes time for the hot gas and dark matter from the halo in which the satellite galaxy was born to be stripped away. Including this delayed stripping of the hot gas halo, without including any other environmental effects (e.g. tidal or ram pressure stripping of the cold gas in satellites) improves satellite statistics in SAMs (Font et al. 2008, Weinmann et al. 2010), though some tension with observations remains (Hirschmann et al. 2014). A particularly curious observational result is “galaxy conformity”, in which halos with red central galaxies preferentially have red satellites (Weinmann et al. 2006a). This effect extends even beyond the virial radius to surrounding centrals, and it is not reproduced at the observed level in SAMs (Kauffmann et al. 2013). It can be reproduced in “age abundance matching” models, an extension of abundance matching that uses halo formation times to assign SFR or colors (Hearin et al. 2014), but the physics that drives conformity remains unclear. Satellite and environmental quenching has not yet been extensively investigated in self-consistent cosmological simulations, but there is clearly much to be learned by doing so and this is an area where much progress can be made in the near future.

4.2. Internal Structure and Kinematics

4.2.1. Formation of Galactic Disks. The longstanding conventional paradigm to explain the origin of galactic disks posits that gas accreting from the halo conserves its specific angular momentum j, thereby settling into a disk (Fall & Efstathiou 1980, Mo et al. 1998). While modern cosmological simulations support this basic paradigm, they suggest that the full story is much more complicated.

The average specific angular momentum of galactic disks is indeed comparable to that expected from conserving the j from the halo (Dalcanton et al. 1997, Dutton & van den Bosch 2012). However, the distribution of j within disks predicted from simple infall is strongly inconsistent with observations, in the sense that observed galaxies have a strong deficit of low-j gas, a mild deficit of high-j gas, and a large excess of intermediate-j gas (van den Bosch et al. 2001, Bullock et al. 2001). This suggests that some process removes low-j gas and deposits it at intermediate-j.

Early numerical hydrodynamic simulations of disk galaxy formation suffered an even more severe “angular momentum catastrophe”, as they produced disks with much lower average j than the halo, indicating that a large amount of j was being lost during the formation process. For many years, simulations were only able to produce very compact disks with large spheroids, and were unable to produce spirals even as late-type as the Milky Way (Steinmetz 1999, Sommer-Larsen et al. 1999, Navarro & Steinmetz 2000). Moreover, these galaxies exhibited centrally-peaked rotation curves in disagreement with observed flat rotation curves, did not lie on the observed Tully-Fisher relation, and formed far too large a fraction of their available baryons into stars. It was gradually realized that the origin of this angular momentum catastrophe lay in too-efficient star formation and gas consumption in small objects at high redshift. These then assembled into low redshift galaxies via relatively gas-poor mergers, which are very efficient at dissipating angular momentum and building spheroids (Maller & Dekel 2002).

Implementing more efficient star formation feedback has proven to be the key to solving all of these problems (e.g. Governato et al. 2007, Guedes et al. 2011). Stellar-driven winds preferentially remove low angular momentum gas from the centers of galaxies, and deposit it in the disk outskirts after re-torquing in the halo (Brook et al. 2012, Übler et al. 2014). Feedback also makes star formation less efficient, keeping galaxies gas rich, which makes disks more resiliant to mergers (Robertson et al. 2006a, Governato et al. 2009). Finally, the baryonic mass of small infalling satellites, particularly at early epochs, is greatly reduced, thereby mitigating early spheroid growth via merging.

Fig. 8 shows a state-of-the-art high resolution zoom-in simulation of a disk galaxy using the GASOLINE code (Christensen et al. 2012). One can see that it is now possible to form very late-type and even bulgeless galaxies (Christensen et al. 2014). The same simulations predict a z = 0 m_star − M_halo relation in agreement with observational constraints (Munshi et al. 2013). In dwarf galaxies, the same “blast wave” feedback model can impulsively heat the dark matter, removing the central cusp generically predicted in dark matter simulations, and thereby producing rotation curves in better agreement with observations (Governato et al. 2010, Pontzen & Governato 2012, Oh et al. 2011). As a bonus, Brooks & Zolotov (2014) have shown that destroying the central cusps in dwarf galaxies leads to enhanced tidal stripping of satellites. The combined effects of energetic stellar feedback and enhanced stripping produces satellites with internal kinematics that agree with observed dwarf spheroidal galaxies in the Local Group, plausibly resolving the “too big to fail” problem pointed out by Boylan-Kolchin et al. (2011). While these successes may be specific to a particular sub-grid model for feedback that may or may not be fully accurate, nonetheless it suggests it is possible to form disk galaxies with realistic properties within a ΛCDM universe provided that the sub-grid treatment of stellar feedback and the ISM possess certain key features. First, stellar feedback must be effective at keeping galaxy-wide star formation efficiencies low, and stellar winds must preferentially remove low-angular momentum material. Second, star formation should occur only in very dense, highly clustered environments like those that are expected to form GMCs, not smoothly distributed over the whole disk, which helps to make stellar feedback more efficient because the star formation is highly clustered as in real galaxies.

Figure 8. Top: Gas surface density and simulated observations of a spiral galaxy formed in a high-resolution zoom-in simulation. Top left: H i gas surface density (gray) and H2 surface density (red). Top middle and right: optical images of stellar emission, showing the galaxy in face-on and edge-on orientations. Middle left: rotation curve for the same initial conditions, but with different sub-grid physics for treating cooling (primordial only vs. metal-line) and the ISM (H2-based cooling and SF). Middle right: distribution of scaled specific angular momentum for the dark matter and baryons in these same simulations. Bottom: star formation histories for the same three models shown in the middle panels. Reproduced from Christensen et al. (2014).

Recent observations of disks during Cosmic Noon have presented new challenges for models. Disks at z ∼ 2 are observed to be substantially puffier, having rotation velocity V_rot divided by gas dispersion σ of ∼ 3 as opposed to ∼ 10 for today’s disks (Förster Schreiber et al. 2009). Many z ∼ 2 disks also have large, bright clumps that comprise a substantial portion of the disk star formation (Guo et al. 2012), though significantly less of the stellar mass (Wuyts et al. 2012), and are generating outflows (Genzel et al. 2011). While most of these objects are sufficiently massive by z ∼ 2 to likely evolve into ellipticals today, lower mass objects that will evolve into today’s disks generally have even higher V_rot / σ. Understanding the origin of these properties and the evolution of the population to z = 0 has become a major cottage industry.

As discussed earlier, ISM pressurization was found to be necessary to stabilize disks against fragmentation (Robertson et al. 2004) and form spiral galaxies like those observed today. With the discovery of clumpy disks at z ∼ 2 (Elmegreen & Elmegreen 2005, Förster Schreiber et al. 2009), the abundant clumps that formed in simulations without ISM pressurization began to be touted as a “feature” (Bournaud et al. 2007, Dekel et al. 2009, Ceverino et al. 2010). However, such models produced overly high stellar fractions, typically ≳ 50% whereas abundance matching constraints suggest a value of ∼ 10−20% (Moster et al. 2010b, Behroozi et al. 2010, Wake et al. 2011). After implementing more efficient stellar feedback due to radiation pressure from young stars, Ceverino et al. (2014) reduced the stellar fractions by a factor of 2–3, but are they are still somewhat high (Moody et al. 2014). Models with significant ISM pressurization, either imposed (Genel et al. 2012) or self-consistently generated (Faucher-Giguère et al. 2013), matched stellar fraction constraints and still produced massive clumps, but these were less prominent and quicker to disrupt.

The clump formation can be understood analytically in the context of the Toomre (1964) Q ≡ c_s Ω / π GΣ, where c_s is the sound speed, Ω is the angular speed, and Σ is the local surface density. If Q < 1 gravitational collapse can overcome shearing disruption, and the region is unstable. Clumps are observed to be regions with Q ≪ 1 (Genzel et al. 2011), and simulations indicate that clumps are unstable regions self-regulated by gravity (Ceverino et al. 2010). The characteristic mass scale for instability is m_clump ≲ 10⁹ M_⊙, in good agreement with observations suggesting clumps up to these masses (Genzel et al. 2011). If this is the basic origin of clumps, then they are expected to become less prominent in disks at later epochs, reducing in mass as disks settle (Dekel et al. 2009). Simulations show that disks do indeed settle towards z = 0, in accord with observations (Kassin et al. 2014). If cosmological accretion drives turbulence in the ISM, then the settling may be due to the decreasing accretion rate at lower redshifts (Genel et al. 2012a), though Hopkins et al. (2013b) argue that accretion does not drive the turbulence in galactic disks. It remains to be demonstrated that a single sub-grid ISM model can simultaneously reproduce the ∼ 10⁹ M_⊙ clumps in turbulent high-z disks along with thin disks with ≲ 10⁶ M_⊙ clumps today like the Milky Way. Nonetheless there is at least a plausible description for the evolution of clumps in disks across cosmic time.

4.2.2. Formation of Spheroid-dominated Galaxies. Since the seminal work of Toomre (1977), it has been recognized that nearly equal mass (“major”) mergers can efficiently remove angular momentum from stellar disks, producing dispersion-dominated spheroids (Toomre 1977, Barnes 1988, Barnes 1992, Hernquist 1992, Hernquist 1993b, Mihos & Hernquist 1996). Unequal mass (“minor”) mergers down to mass ratios of ∼ 1:10 can thicken disks and build up the spheroid component of galaxies (Walker et al. 1996, Moster et al. 2010a). Mergers are expected to be ubiquitous in the hierarchical CDM paradigm. Thus the most basic picture of the origin of the two dominant classes of galaxy morphologies is that smooth accretion of gas produces disks, and mergers destroy disks and build spheroid-dominated galaxies. A merger-driven formation mechanism for spheroid-dominated galaxies has been implemented in most SAMs since the earliest such models (Kauffmann et al. 1993, Kauffmann 1996, Baugh et al. 1996, Somerville & Primack 1999), motivated by the studies based on binary mergers simulated with numerical hydrodynamics. These early works and others over the past decade (e.g. De Lucia et al. 2006, Parry et al. 2009) have shown that this picture can qualitatively reproduce many of the observed correlations pertaining to galaxy morphology, namely, spheroid dominated galaxies are predicted to be more massive, more common in massive halos, redder, and to have older stellar populations. In empirical support of this picture, it has been shown that the observed rate of mergers derived from pair counts and visually identified interacting galaxies is in plausible statistical agreement with the build-up of the quiescent, spheroid-dominated population (Robaina et al. 2010, Hopkins et al. 2008a).

More recent work has led to a refinement of the merger picture. Numerical hydrodynamic simulations showed that gas-rich mergers do not drive efficient angular momentum loss, and so lead to re-formation of disk-dominated galaxies (Robertson et al. 2004, Robertson et al. 2006a, Hopkins et al. 2009a). In addition, following the formation of a spheroid via a merger, newly accreted gas can re-form a disk. Thus, a picture has developed in which morphological transformation and morphological demographics are intimately linked with feedback and quenching. It is known that the massive early-type galaxies in the local universe formed most of their stars at least 8-10 Gyr ago, around z ∼ 2–4 (Trager et al. 2000, Thomas et al. 2005). We also know that the average massive star-forming galaxies at z ∼ 2 are quite gas rich (Tacconi et al. 2013, Genzel et al. 2014). Thus, in order to produce a spheroid-dominated population at z = 0, some process had to consume or remove much of the gas from their progenitors before they merged, and prevent significant amounts of new gas from cooling. This appears to point qualitatively towards a combination of “ejective” and “preventative” feedback, perhaps linked with two different modes of AGN feedback.

It has been suggested that spheroids may also form and grow in situ due to internal gravitational instabilities. There are two different kinds of internal processes that may grow bulges, which are frequently grouped together under the term “disk instabilities”, but which are physically quite distinct and are thought to produce fundamentally different kinds of bulges. We have already discussed the formation of giant clumps in Toomre-unstable disks (see Section 4.2.1), sometimes called “violent disk instabilities” (Dekel et al. 2009). If these clumps survive and migrate to the galaxy center, they may form a classical bulge (Elmegreen et al. 2008, Dekel et al. 2009, Bournaud et al. 2011). However, there remains some debate about the importance of clumps in feeding spheroid growth. Simulations implementing kinetic feedback that were able to match m_star − M_halo constraints suggested that clumps mostly disrupt before reaching the center (Genel et al. 2012b). Hopkins et al. 2012a also found that in simulations of isolated disks (not cosmological) with a suite of physically motivated stellar feedback physics, even large clumps mostly blow themselves apart while in the disk, thereby only modestly contributing to spheroid growth. However, some recent simulations suggest that clumps can survive substantially longer than a disk dynamical time and grow a spheroid (Mandelker et al. 2014, Bournaud et al. 2014). Comparing stellar and SFR maps, (Wuyts et al. 2012) showed that clump lifetimes are ∼ 100−200 Myr, which would suggest disruption unless inward migration can occur on a single dynamical time or less, but radial age gradients of clumps suggest somewhat longer lifetimes (Genzel et al. 2011). Additionally, as the giant clumps orbit within the disk, even if they disrupt before reaching the center, they may drive inflows of gas into the galaxy nucleus, via the same sort of physics as merger-induced nuclear inflows (Bournaud et al. 2011).

The other process that is referred to as a “disk instability” is not really a (global) instability at all. It involves the secular transfer of mass into a compact, dynamically hot component via the formation of a bar (Toomre 1964, Hohl 1971, Ostriker & Peebles 1973, Combes et al. 1990). The topic of galactic bars is largely outside of the scope of this review, but a few points are worth briefly noting. First, viewed side-on, bars may be identified as “boxy bulges” (our Galaxy is a familiar example), but if viewed face-on these structures would not be identified as bulges (Combes et al. 1990). It is generally impossible to robustly distinguish bars from bulges in distant galaxies. Second, secular processes can redistribute angular momentum and mass within the disk, building a pseudobulge (Kormendy & Kennicutt 2004, Kormendy 2013). In constrast to the violent disk instabilities described above, the disk essentially remains in dynamical equilibrium during this secular evolution. The fundamental differences between classical bulges and pseudobulges are briefly summarized in Section 4.2, and a much more complete discussion is given in Kormendy & Kennicutt (2004). The stronger correlation between black hole mass and classical bulge mass recently emphasized by Kormendy & Ho (2013) is presumably evidence that the processes that build classical bulges (mergers and violent disk instabilities) are most closely connected with black hole fueling.

4.2.3. Demographics of Spheroid- and Disk-Dominated Galaxies. Explaining the demographics of galaxies of different morphologies is another challenge for theory. Detailed quantitative statistical comparisons between the predictions of cosmological simulations and observations of galaxy morphological demographics are difficult, because up until now, most observational studies of galaxy morphology have used classifiers that are not straightforward for models to predict. Semi-analytic models predict the fraction of stellar mass or light in a spheroid component (B / T), while most observational studies use visual morphological classification or statistics such as Sersic index or concentration. A few observational studies have carried out decompositions into spheroid and disk contributions (Simard et al. 2011, Gadotti & Kauffmann 2009, Bluck et al. 2014), but there are large uncertainties in these decompositions as well (see e.g. Tasca & White 2011, Benson et al. 2007). There is a large dispersion in observational estimates of galaxy morphological demographics derived from different surveys and classification methods.

A number of studies have compared the predictions of SAMs with observational estimates of luminosity or stellar mass functions divided by galaxy morphology, or with the fraction of disk- or spheroid-dominated galaxies as a function of stellar mass (e.g. Benson et al. 2007, Parry et al. 2009, Guo et al. 2011, Porter et al. 2014). These studies all found fairly good agreement between the predictions of these different SAMs and the observations, but interestingly the dominant mechanism that drives spheroid growth is different in different models, as we discuss further below.

Although the details of the prescriptions differ, all semi-analytic models that attempt to track galaxy morphology assume that mergers destroy disks and build spheroids. However SAM-based studies have found, to varying degrees, that non-merger related mechanisms for spheroid growth may be needed. The most commonly invoked alternative to mergers is a “disk instability” mode as described above. This is assumed to occur when the mass in the disk exceeds a critical value that depends on the angular momentum of the disk material. The implementation of this process varies widely between models, leading to significantly differing conclusions about its importance. The GALFORM SAMs assume that when a disk becomes unstable, all of the stars and gas in the disk are moved to a spheroid component. They find that these disk instabilities are the dominant channel for spheroid growth except at the highest stellar masses (Parry et al. 2009). Other SAMs (De Lucia & Blaizot 2007, Guo et al. 2011, Porter et al. 2014) make a more moderate assumption, that just enough stars or stars and gas are moved from the disk to the spheroid to return the system to stability. These models find that disk instabilities appear to be needed to reproduce the observed numbers of spheroid dominated galaxies at intermediate masses (Porter et al. 2014), but are sub-dominant in driving spheroid growth at all masses. An important and apparently robust prediction is that models with a “disk instability” driven channel for spheroid growth appear to form massive spheroids earlier than models in which spheroids form only via mergers (De Lucia et al. 2011, Porter et al. 2014). These predictions can now be confronted with observations from the new generation of medium-deep surveys with HST (Brennan et al. in prep).

The flip side of producing enough spheroid dominated galaxies is the challenge of producing galaxies that are close to pure disks, which are perhaps surprisingly frequently observed in the real Universe (Kormendy et al. 2010, Fisher & Drory 2011). If mergers destroy disks and build spheroids, and nearly all halos of all masses have experienced mergers during the course of their formation history, as predicted by ΛCDM, is it possible to reconcile the existence of these objects with the ΛCDM picture? Hopkins et al. (2009) showed that including the suppression of disk destruction in mergers with high gas fraction progenitors alleviates this problem, bringing predictions into agreement with observations in a semi-analytic model — the majority of mergers occur at high redshift when galaxy gas fractions are expected to have been fairly high. Furthermore, Moster et al. (2010a, 2012) showed that accounting for the presence of both cold gas in the disk and hot gas in the halo decreases disk heating due to minor mergers by a factor of 2–3 relative to previous calculations that included dissipationless components (stars and dark matter) only. However, Porter et al. (2014) showed that adding a disk instability driven channel for spheroid formation, tuned to reproduce the abundances of spheroid-dominated galaxies, may leave behind too few objects with extremely low B / T ≲ 0.2. Detailed studies with larger samples of galaxies simulated at high resolution in a full cosmological context are required to determine whether this is truly a fundamental problem for ΛCDM, but it remains a serious concern.

Extensive detailed predictions on morphological demographics from numerical cosmological simulations have not yet appeared in the literature. Such studies should be possible with the new generation of simulations, and detailed analysis of these simulations should help shed light on the physical mechanisms that are responsible for shaping galaxy morphology.

4.2.4. Structural Scaling Relations. The existence of structural scaling relations for galaxies, the relationship between the structure of disks and spheroids at a given mass scale, and the evolution of these relations over cosmic time, encode crucial information about galaxy formation and provide stringent constraints for models.

What physics determines the internal structure of galaxies? The most basic picture is that dark matter and diffuse gas acquire angular momentum through tidal torques and mergers (Peebles 1969, Vitvitska et al. 2002), leading to dark matter and gaseous halos with a broad log-normal distribution of spin parameters. The dimensionless spin parameter is usually defined as

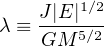where M, J, and E are the mass, angular momentum, and total energy of the system, respectively (MvdBW, p. 502). If we assume, perhaps naïvely, that the halo gas conserves its angular momentum as it cools and collapses to form a disk, and that the post-collapse disk surface density profile has an exponential form, then the disk scale radius will be given by

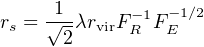where r_vir is the virial radius of the halo, and F_R and F_e are functions that account for the initial density profile of the dark matter halo and the contraction of the inner halo due to the increased gravitational force after the gas falls in (Mo et al. 1998). The rotation velocity can then be calculated by adding the contribution of the exponential disk and the contracted halo in quadrature.

In spite of its simplicity, this model does remarkably well at reproducing the size-mass relation for disk galaxies and its evolution since z ∼ 2 (Somerville et al. 2008, Firmani & Avila-Reese 2009, Dutton et al. 2011). Recently, high-resolution numerical hydro simulations have also been shown to be quite successful at reproducing the size-mass relation for galactic disks and its evolution (Brooks et al. 2011, Aumer et al. 2013). As discussed above, hydro simulations have only recently been able to successfully reproduce disk sizes, and including strong star formation driven outflows that preferentially remove the low angular momentum material appears to be a crucial component of this success. Recent simulations suggest that accretion by “cold streams” may bring most of the gas into galaxies, with an average specific angular momentum that is a factor of ∼ 2–3 higher than that of the dark matter halo (Stewart et al. 2013). About a factor of 2–3 of this angular momentum is then lost via torques within the mis-aligned disk and via outflows (Danovich et al. 2014). The success of the simple model for predicting disk sizes may therefore be simply a happy accident.

Much of the convincing evidence for the importance of mergers in producing spheroid-dominated galaxies comes from the success of merger simulations in reproducing structural properties of classical bulges and elliptical galaxies. For example, early work Hernquist (1992), Barnes (1992) showed that mergers transform rotationally supported disks with exponential light profiles into slowly rotating remnants with luminosity profiles that are well-described by an r^1/4 form over a large radial range. More recently, it has been shown that remnants of binary disk mergers lie on the observed fundamental plane (Robertson et al. 2006b, Hopkins et al. 2009b).

A striking recent observation is that, at fixed stellar mass, spheroid-dominated galaxies at z ∼ 2 have much smaller sizes and central densities higher by orders of magnitude compared to today’s (e.g. Trujillo et al. 2006, van Dokkum et al. 2008, van Dokkum et al. 2014, van der Wel et al. 2014, Barro et al. 2013). For dissipationless (dry) mergers on parabolic orbits (hence with small orbital energy), energy conservation and the virial theorem can be used to show that, given a progenitor mass ratio η ≤ 1 and ratio of squares of their velocity dispersions of є ≤ 1, the ratio of final to initial radius is given by

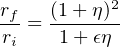(9)

(Naab et al. 2009). For a 1:1 merger, η = є = 1, hence r_f / r_i = 2, which leads to a modest surface density reduction of a factor of four. One can show that, for a given total mass increase, the size is increased much more by a series of minor mergers than by a single major one. Numerical simulations confirm such a size increase in dissipationless mergers, which generally move galaxies along the mass-size relation (Boylan-Kolchin et al. 2005). This can reproduce the observed size increase and central density reduction (Naab et al. 2009, Oser et al. 2012) since z ∼ 2 for cosmologically-plausible merger histories (Gabor & Davé 2012), via minor mergers depositing material predominantly in the outskirts.

If disks (star forming galaxies) are continuously being transformed into spheroids (quiescent galaxies), as the demographic observations indicate (see Section 1.1), how then can we understand the very different slopes and evolution of the size-mass relationship for disks and spheroids? Several recent works have pointed out that accounting for the effects of dissipation in gas-rich mergers, can lead to important changes in the scaling relations (Covington et al. 2008, Hopkins et al. 2009b, Hopkins et al. 2010, Shankar et al. 2010, Shankar et al. 2013, Covington et al. 2011, Porter et al. 2014). In the presence of gas, energy is dissipated, which can lead to merger remnants that are smaller and denser than their progenitors. Porter et al. (2014) implemented a recipe for computing spheroid sizes and velocity dispersions based on a simple analytic model including the effects of gas dissipation, tuned to binary merger simulations, self-consistently within the Santa Cruz SAM. They showed that without any tuning the model predicts rapid size evolution of spheroid-dominated galaxies since z ∼ 2, along with the weaker evolution in the Faber-Jackson relation, in very good quantitative agreement with the observed structural relations.

In this picture, dissipation plays a major role in explaining the different slope, scatter, and evolution of the size-mass relation for spheroid dominated (quiescent) galaxies relative to disks. Lower mass spheroids have lower mass progenitors, which have higher gas fractions at all redshifts. More gas means more dissipation and smaller remnants, thus a steeper size-mass relation. Progenitors at higher redshifts have higher gas fractions than those at lower redshift, so the size-mass relation for spheroids “tilts away” from that for disks more, contributing to more rapid size evolution especially for the lower-mass spheroids. The decrease in scatter occurs because disks with higher angular momentum have larger radii and lower gas densities, resulting in less efficient star formation. These large radius disks therefore end up with higher gas fractions, and experience more dissipation when they merge, producing smaller remnants. Similarly, the observed tilt of the Fundamental Plane can be explained by the expected trends in galaxy gas content with mass and redshift, and the physics of gas dissipation in mergers (Hopkins et al. 2009b, Covington et al. 2011, Porter et al. 2014).

⁴ The stellar masses in the GALFORM models have been multiplied by a factor of 1.23 to convert from a Kennicutt to a Chabrier IMF (Mitchell, Lacey, Baugh & Cole 2013). Back.