

© CAMBRIDGE UNIVERSITY PRESS 1999
| |
1.6.7 Inflation Summary
The key features of all inflation scenarios are a period of superluminal expansion, followed by (``re-'')heating which converts the energy stored in the inflaton field (for example) into the thermal energy of the hot big bang.
Inflation is generic: it fits into many versions of particle
physics, and it can even be made rather natural in modern supersymmetric
theories as we have seen. The simplest models have inflated away all
relics of any pre-inflationary era and result in a flat universe after
inflation, i.e.,  = 1 (or more
generally
= 1 (or more
generally  0 +
0 + 
 = 1). Inflation also produces scalar (density) fluctuations that
have a primordial spectrum
= 1). Inflation also produces scalar (density) fluctuations that
have a primordial spectrum
where V is the inflaton potential and np is the
primordial spectral
index, which is expected to be near unity (near-Zel'dovich spectrum).
Inflation also produces tensor (gravity wave) fluctuations, with spectrum
where the tensor spectral index nt
The quantity (1 - np) is often called the ``tilt'' of
the spectrum;
the larger the tilt, the more fluctuations on small spatial scales
(corresponding to large k) are suppressed compared to those on
larger scales. The scalar and tensor waves are generated by
independent quantum fluctuations during inflation, and so their
contributions to the CMB temperature fluctuations add in quadrature.
The ratio of these contributions to the quadrupole anisotropy
amplitude Q is often called T/S
On the other hand, inflation is also Alice's restaurant where,
according to the Arlo Guthrie song, ``...you can get anything you
want ... excepting Alice''. It's not even clear what ``Alice'' you can't
get from inflation. It was initially believed that inflation predicts a
flat universe. But now we know that you
And in many versions of inflation, the most reasonable answer to the
question ``what happened before inflation'' appears to be eternal
inflation, which implies that in most of the meta-universe,
exponentially far beyond our horizon, inflation never stopped.
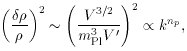
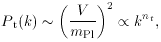
 (1 - np) in
many models.
(1 - np) in
many models.
 Qt2 / Qs2; thus the
primordial scalar fluctuation power is decreased by the ratio
1 / (1 + T/S) for the same COBE normalization, compared to the situation
with no gravity waves (T = 0). In power-law inflation,
T/S = 7(1 - np). This is an approximate
equality in other popular
inflation models such as chaotic inflation with
V(
Qt2 / Qs2; thus the
primordial scalar fluctuation power is decreased by the ratio
1 / (1 + T/S) for the same COBE normalization, compared to the situation
with no gravity waves (T = 0). In power-law inflation,
T/S = 7(1 - np). This is an approximate
equality in other popular
inflation models such as chaotic inflation with
V( ) =
m2
) =
m2  2
or
2
or 
 4. But note that the tensor
wave amplitude is just
the inflaton potential during inflation divided by the Planck mass, so
the gravity wave contribution is negligible in theories like the
supersymmetric model discussed above in which inflation occurs at an
energy scale far below mPl. Because gravity waves
just redshift
after they come inside the horizon, the tensor contributions to CMB
anisotropies corresponding to angular wavenumbers
4. But note that the tensor
wave amplitude is just
the inflaton potential during inflation divided by the Planck mass, so
the gravity wave contribution is negligible in theories like the
supersymmetric model discussed above in which inflation occurs at an
energy scale far below mPl. Because gravity waves
just redshift
after they come inside the horizon, the tensor contributions to CMB
anisotropies corresponding to angular wavenumbers
 >> 20, which
came inside the horizon long ago, are strongly suppressed compared to
those of scalar fluctuations. The indications from presently available data
(Netterfield et
al. 1997;
cf. Tegmark 1996,
and Silk's article in this volume) are that the CMB amplitude is rather
high for
>> 20, which
came inside the horizon long ago, are strongly suppressed compared to
those of scalar fluctuations. The indications from presently available data
(Netterfield et
al. 1997;
cf. Tegmark 1996,
and Silk's article in this volume) are that the CMB amplitude is rather
high for 
 200, approximately in
agreement with the predictions of
standard CDM with h
200, approximately in
agreement with the predictions of
standard CDM with h  0.5,
0.5,  b
b  0.1, and scalar
spectral index np = 1. This suggests that there is
little room for
gravity-wave contributions to the low-
0.1, and scalar
spectral index np = 1. This suggests that there is
little room for
gravity-wave contributions to the low- CMB anisotropies, i.e.,
that T/S << 1. Thus tests of inflation involving the gravity-wave
spectrum will be very difficult. Fortunately, inflation can be tested
with the data expected soon from the next generation of CMB
experiments, since it makes very specific and discriminatory
predictions regarding the relative locations of the acoustic peaks in
the spectrum, for example the ratio of the first peak location
to the spacing between the peaks
CMB anisotropies, i.e.,
that T/S << 1. Thus tests of inflation involving the gravity-wave
spectrum will be very difficult. Fortunately, inflation can be tested
with the data expected soon from the next generation of CMB
experiments, since it makes very specific and discriminatory
predictions regarding the relative locations of the acoustic peaks in
the spectrum, for example the ratio of the first peak location
to the spacing between the peaks  1 /
1 / 

 0.7-0.9
(Hu & White 1996,
Hu et al. 1997).
0.7-0.9
(Hu & White 1996,
Hu et al. 1997).
 0 < 1
(with
0 < 1
(with  = 0), as discussed in
the previous section.
= 0), as discussed in
the previous section.
 0, a low
reheat temperature implying no production
of topological defects and presumably requiring that baryosynthesis occur
at the electroweak phase transition, and plenty of inflation implying
that
0, a low
reheat temperature implying no production
of topological defects and presumably requiring that baryosynthesis occur
at the electroweak phase transition, and plenty of inflation implying
that  0
0
 1.
1.