© CAMBRIDGE UNIVERSITY PRESS 1999

1.7 Comparing DM Models to Observations: CDM vs. CHDM

1.7.1 Building a Cosmology: Overview

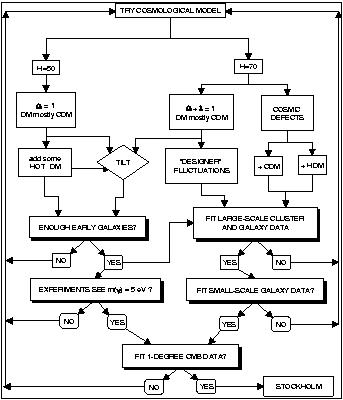
An effort has been made to summarize the main issues in cosmological model-building in Figure 1.3. Here the choices of cosmological parameters, dark matter composition, and initial fluctuations that specify the model are shown at the top of the chart, and the types of data that each cosmological model must properly predict are shown in the boxes with shaded borders in the lower part of the chart. Of course, the chart only shows a few of the possibilities. Models in which structure arises from gravitational collapse of adiabatic inflationary fluctuations and in which most of the dark matter is cold are very predictive. Since such models have also been studied in greatest detail, this class of models will be the center of attention here.

Figure 1.3. Building a Cosmological Model. (This figure was inspired by similar flow-charts on inventing dark matter candidates, by David Weinberg and friends, and by Rocky Kolb.)

Perhaps the most decisive issue in model building is the value of the cosmological expansion rate, the Hubble parameter h. If h 0.7 as some observers still advocate, and the age of the universe t₀ 13 Gyr, then only low-₀ models can be consistent with general relativity. ⁽⁴⁾ Depending on just how large h and t₀ are, a positive cosmological constant may also be necessary for consistency with GR, since even in a universe with -> 0 the age t₀ -> H₀^-1 = 9.78 h^-1 Gyr (see Figure 1.1). Thus, with = 0 and ₀ -> 0, h < 0.75 (13 Gyr / t₀). The upper limit on h is stronger, the larger ₀ is: with = 0 and ₀ 0.3, h < 0.61 (13 Gyr / t₀); with = 0 and ₀ 0.5, h < 0.57 (13 Gyr / t₀). It has been argued above that the evidence strongly suggests that ₀ 0.3, especially if the initial fluctuations were Gaussian; thus, if we assume values of h = 0.7 and t₀ = 13 Gyr, we must include a positive cosmological constant. For definiteness, the specific choice shown is ₀ + = 1, corresponding to the flat cosmology inspired by standard inflation.

In such a CDM model, one might initially try the Zel'dovich primordial fluctuation spectrum, i.e. P_s(k) = A_s k^n_p with n_p = 1. However, this might not predict the observed abundance of clusters when the amplitude of the spectrum is adjusted to agree with the COBE data on large scales. If ₀ > 0.3, then COBE-normalized CDM predicts more rich clusters than are actually observed. In that case, it will be necessary to change the spectrum. The simplest way to do that is to add some ``tilt'' - i.e., assume that n<sub>p</sub> < 1. This adds one additional parameter. One can also consider more complicated ``designer'' primordial spectra with two or more parameters, which as I have mentioned can also be produced by inflation. In any case, it is then also necessary to check that the large-scale cluster and galaxy correlations on large scales are also in agreement with experiment. As we will see, this is indeed the case for typical CDM models. In order to see whether such a model also correctly predicts the galaxy distribution on smaller spatial scales 10 h^-1 Mpc, on which the fluctuations in the number counts of galaxies N_g are nonlinear - i.e., (N_g / N_g)_rms 1 - it is necessary to do N-body simulations. As we will discuss, these are probably rather accurate in showing the distribution of dark matter on intermediate scales. But simulations are not entirely reliable on the scales of clusters, groups, and individual galaxies since even the best available simulations include only part of the complicated physics of galaxy formation, and omit or treat superficially crucial aspects such as the feedback from supernovae. Thus one of the main limitations of simulations is ``galaxy identification'' - locating the likely sites of galaxies in the simulations, and assigning them appropriate morphologies and luminosities.

If h 0.5 and t₀ 13 Gyr, or if h 0.6 and t₀ 11 Gyr, then models with critical density, = 1, are allowed. Since the COBE-normalized CDM model greatly overproduces clusters, it will be necessary to make some modification to decrease the fluctuation power on cluster scales - for example, tilt the spectrum or change the assumed dark matter composition. As we have discussed, hot dark matter cannot preserve fluctuations on small scales, so adding a little hot dark matter to the mix of cold dark matter and baryons will indeed decrease the amount of cluster-scale power. A possible problem is that tilting or adding hot dark matter will also decrease the amount of power on small scales, which means that protogalaxies will form at lower redshift. So such models must be checked against data indicating the amount of small-scale structure at redshifts z 3 - for example, against the abundance of neutral hydrogen in damped Lyman absorption systems in quasar spectra, or the protogalaxies seen in emission at high redshift. Acceptable models must of course also fit the data on large and small-scale galaxy distributions. As we will see, = 1 COBE-normalized models with a mixture of Cold and Hot Dark Matter (CHDM) can do this if the hot fraction 0.2.

The ultimate test for all such cosmological models is whether they will agree with the CMB anisotropies on scales of a degree and below. Such data is just beginning to become available from ground-based and balloon-borne experiments, and continuing improvements in the techniques and instruments insure that the CMB data will become steadily more abundant and accurate. CMB maps of the whole sky must come from satellites, and it is great news for cosmology that NASA has approved the MAP satellite which is expected to be ready for launch by 2001, and that the European Space Agency is planning the even more ambitious COBRAS/SAMBA satellite, recently renamed Planck, to be launched a few years later.

Both sorts of models that have been discussed, = 1 tilted CDM (TCDM) or CHDM, and ₀ + = 1 CDM - are simple, one-parameter modifications of the original standard CDM model. The astrophysics community has been encouraged by the great initial success of this theory in explaining the existence of galaxies and fitting galaxy and cluster data (BFPR, DEFW), and the fact that biased CDM only missed predicting the COBE observations by a factor of about 2. The other reason why the CDM-variant models have been studied in much more detail than other cosmological models is that they are so predictive: they predict the entire dark matter distribution in terms of only one or two model parameters (in addition to the usual cosmological parameters), unlike non-Gaussian models based on randomly located seeds, for example. Of course, despite the relatively good agreement between observations and the predictions of the best CDM variants, there is no guarantee that such models will ultimately be successful.

Although the cosmic defect models (cosmic strings, textures) are in principle specified in terms of only a small number of parameters (in the case of cosmic strings, the string tension parameter Gµ plus perhaps a couple of parameters specifying aspects of the evolution of the string network), in practice it has not yet been possible for any group to work out the predicted galaxy distribution in such models. Most proponents of cosmic defect models have assumed an = 1, H₀ 50 cosmology, but the chart refers instead to a cosmic defects option under H₀ = 70. This is done because it would be worthwhile to work out a low- case as well, since in defect models there is less motivation to assume the inflation-inspired flat (₀ + = 1) cosmology.