© CAMBRIDGE UNIVERSITY PRESS 1999

1.7.4 Numerical Simulations to Probe Smaller Scales

``Standard'' = 1 Cold Dark Matter (SCDM) with h 0.5 and a near-Zel'dovich spectrum of primordial fluctuations (Blumenthal et al. 1984) until a few years ago seemed to many theorists to be the most attractive of all modern cosmological models. But although SCDM normalized to COBE nicely fits the amplitude of the large-scale flows of galaxies measured with galaxy peculiar velocity data (Dekel 1994), it does not fit the data on smaller scales: it predicts far too many clusters (White, Efstathiou, & Frenk 1993) and does not account for their large-scale correlations (e.g. Olivier et al. 1993, Borgani et al. 1997), and the shape of the power spectrum P (k) is wrong (Baugh & Efstathiou 1994, Zaroubi et al. 1996). But as discussed above, variants of SCDM can do better. Here the focus is on CHDM and CDM. The linear matter power spectra for these two models are compared in Fig. 1.8 to the real-space galaxy power spectrum obtained from the two-dimensional APM galaxy power spectrum (Baugh & Efstathiou 1994), which in view of the uncertainties is not in serious disagreement with either model for 10^-2 k 1 h Mpc^-1. The CDM and CHDM models essentially bracket the range of power spectra in currently popular cosmological models that are variants of CDM.

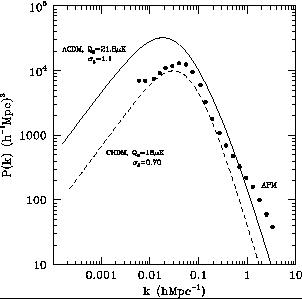
Figure 1.8. Power spectrum of dark matter for CDM and CHDM models considered here, both normalized to COBE, compared to the APM galaxy real-space power spectrum. (CDM: 0 = 0.3, = 0.7, h = 0.7, thus t0 = 13.4 Gy; CHDM: = 1, = 0.2 in N = 2 species, h = 0.5, thus t0 = 13 Gy; both models fit cluster abundance with no tilt, i.e., np = 1. (From Primack & Klypin 1996.)

The Void Probability Function (VPF) is the probability P₀(r) of finding no bright galaxy in a randomly placed sphere of radius r. It has been shown that CHDM with = 0.3 predicts a VPF larger than observations indicate (Ghigna et al. 1994), but newer results based on our = 0.2 simulations in which the neutrino mass is shared equally between N = 2 neutrino species (PHKC95) show that the VPF for this model is in excellent agreement with observations (Ghigna et al. 1997), as shown in Fig. 1.9. However, our simulations (Klypin, Primack, & Holtzman 1996, hereafter KPH96) of COBE-normalized CDM with h = 0.7 and ₀ = 0.3 lead to a VPF that is too large to be compatible with a straightforward interpretation of the data. Acceptable CDM models probably need to have ₀ > 0.3 and h < 0.7, as discussed further below.

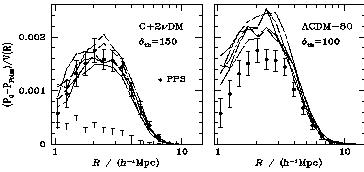
Figure 1.9. Void Probability Function P0(R) for (left panel) CHDM with h = 0.5 and = 0.2 in N = 2 species of neutrinos and (right panel) CDM with h = 0.7 and 0 = 0.3. What is plotted here is difference between the actual VPF and that for a Poisson distribution, divided by V(R) = 4 R3 / 3. Each plot shows also P0(R) for five typical different locations in the simulations (dotted lines) to give an indication of the sky variance. Data points are the VPF from the Perseus-Pisces Survey, with 3 error bars; the VPF from the CfA2 survey is very similar. We have chosen the th for which the P0 of each model best approaches the observational data. In the top-left panel, the heavy ``T'' symbols at the bottom sets the boundary of the region where the signal is indistinguishable from Poissonian. They are obtained from the 3 scatters among measures for 50 different realizations of the Poissonian distribution in the same volume as our samples. (From Ghigna et al. 1997.)

Another consequence of the reduced power in CHDM on small scales is that structure formation is more recent in CHDM than in CDM. As discussed above (in Section 1.4.7), this may conflict with observations of damped Lyman systems in quasar spectra, and other observations of protogalaxies at high redshift, although the available evidence does not yet permit a clear decision on this (see below). While the original = 0.3 CHDM model (Davis, Summers, & Schlegel 1992, Klypin et al. 1993) certainly predicts far less neutral hydrogen in damped Lyman systems (identified as protogalaxies with circular velocities V_c 50 km s^-1) than is observed, as discussed already, lowering the hot fraction to 0.2 dramatically improves this (Klypin et al. 1995). Also, the evidence from preliminary data of a fall-off of the amount of neutral hydrogen in damped Lyman systems for z 3 (Storrie-Lombardi et al. 1996) is in accord with predictions of CHDM (Klypin et al. 1995).

However, as for all = 1 models, h 0.55 implies t₀ 12 Gyr, which conflicts with the pre-Hipparcos age estimates from globular clusters. The only way to accommodate both large h and large t₀ within the standard FRW framework of General Relativity, if in fact both h 0.65 and t₀ 13 Gyr, is to introduce a positive cosmological constant ( > 0). Low-₀ models with = 0 don't help much with t₀, and anyway are disfavored by the latest small-angle cosmic microwave anisotropy data (Netterfield et al. 1997, Scott et al. 1996, Lineweaver & Barbosa 1997; cf. Ganga, Ratra, & Sugiyama 1996 for a contrary view).

CDM flat cosmological models with ₀ = 1 - 0.3, where / (3H₀²), were discussed as an alternative to = 1 CDM since the beginning of CDM (Blumenthal et al. 1984, Peebles 1984, Davis et al. 1985). They have been advocated more recently (e.g., Efstathiou, Sutherland, & Maddox 1990; Kofman, Gnedin, & Bahcall 1993; Ostriker & Steinhardt 1995; Krauss & Turner 1995) both because they can solve the H₀ - t₀ problem and because they predict a larger fraction of baryons in galaxy clusters than = 1 models (this is discussed in Section 1.4.5 above).

Early galaxy formation also is often considered to be a desirable feature of these models. But early galaxy formation implies that fluctuations on scales of a few Mpc spent more time in the nonlinear regime, as compared with CHDM models. As has been known for a long time, this results in excessive clustering on small scales. It has been found that a typical CDM model with h= 0.7 and ₀ = 0.3, normalized to COBE on large scales (this fixes ₈ 1.1 for this model), is compatible with the number-density of galaxy clusters (Borgani et al. 1997), but predicts a power spectrum of galaxy clustering in real space that is much too high for wavenumbers k = (0.4-1)h / Mpc (KPH96). This conclusion holds if we assume either that galaxies trace the dark matter, or just that a region with higher density produces more galaxies than a region with lower density. One can see immediately from Fig. 1.7 and Fig. 1.8 that there will be a problem with this CDM model, since the APM power spectrum is approximately equal to the linear power spectrum at wavenumber k 0.6 h Mpc^-1, so there is no room for the extra power that nonlinear evolution certainly produces on this scale - illustrated in Fig. 1.10 for CDM and in Fig. 1.11 for CHDM. The only way to reconcile the ₀= 0.3 CDM model considered here with the observed power spectrum is to assume that some mechanism causes strong anti-biasing - i.e., that regions with high dark matter density produce fewer galaxies than regions with low density. While theoretically possible, this seems very unlikely; biasing rather than anti-biasing is expected, especially on small scales (e.g., Kauffmann, Nusser, & Steinmetz 1997). Numerical hydro + N-body simulations that incorporate effects of UV radiation, star formation, and supernovae explosions (Yepes et al. 1997) do not show any antibias of luminous matter relative to the dark matter.

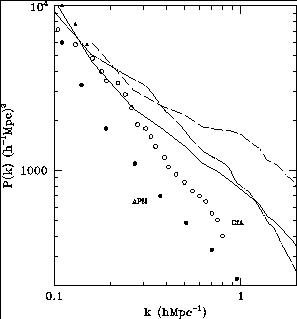
Figure 1.10. Comparison of the nonlinear power spectrum in the 0 = 0.3, h = 0.7 CDM model with observational results. Dots are results for the APM galaxy survey. Results for the real-space power spectrum for the CfA survey are shown as open circle (101 h-1 Mpc sample) and triangles (130 h-1 Mpc sample). Formal error bars for each of the surveys are smaller than the difference between the open and filled points, which should probably be regarded as a more realistic estimate of the range of uncertainty. The full curve represents the power spectrum of the dark matter. Lower limits on the power spectrum of galaxies predicted by the CDM model are shown as the dashed curve (higher resolution CDMf simulation in KPH96) and the dot-dashed curve (lower resolution CDMc simulation).

Our motivation to investigate this particular CDM model was to have H₀ as large as might possibly be allowed in the CDM class of models, which in turn forces ₀ to be rather small in order to have t₀ 13 Gyr. There is little room to lower the normalization of this CDM model by tilting the primordial power spectrum P_p(k) = Ak^n_p (i.e., assuming n_p significantly smaller than the ``Zel'dovich'' value n_p = 1), since then the fit to data on intermediate scales will be unacceptable - e.g., the number density of clusters will be too small (KPH96). Tilted CDM models with higher ₀, and therefore lower H₀ for t₀ 13 Gyr, appear to have a better hope of fitting the available data, based on comparing quasi-linear calculations to the data (KPH96, Liddle et al. 1996c). But all models with a cosmological constant large enough to help significantly with the H₀ - t₀ problem are in trouble with the observations summarized above providing strong upper limits on : gravitational lensing, HST number counts of elliptical galaxies, and especially the preliminary results from measurements using high-redshift Type Ia supernovae.

It is instructive to compare the ₀ = 0.3, h = 0.7 CDM model that we have been considering with standard CDM and with CHDM. At k = 0.5 h Mpc^-1, Figures 5 and 6 of Klypin, Nolthenius, & Primack (1997) show that the = 0.3 CHDM spectrum and that of a biased CDM model with the same ₈ = 0.67 are both in good agreement with the values indicated for the power spectrum P (k) by the APM and CfA data, while the CDM spectrum with ₈ = 1 is higher by about a factor of two. As Fig. 11 shows, CHDM with = 0.2 in two neutrino species (PHKC95) also gives nonlinear P (k) consistent with the APM data.

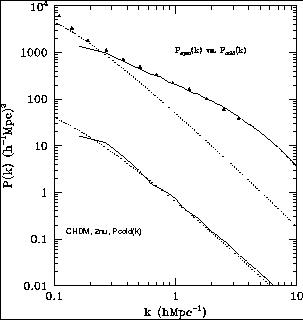
Figure 1.11. Comparison of APM galaxy power spectrum (triangles) with nonlinear cold particle power spectrum from CHDM model considered in this paper (upper solid curve). The dotted curves are linear theory; upper curves are for z = 0, lower curves correspond to the higher redshift z = 9.9. (From Primack & Klypin 1996.)