The theory of the anisotropies in the CMB is rich with details about the
contents and structure of the early universe. Consequently, this theory
can become quite complicated. However, because of this same richness,
this branch of cosmology holds the potential to provide meaningful
constraints on a very large number of quantities of cosmological
interest. Our focus here is to provide the reader with a conceptual
understanding of why and how CMB anisotriopies can be used to determine
cosmological parameters. We will place particular emphasis on the
density parameters corresponding to the spatial curvature of the
universe 
k,
and the baryon density
b. The
reader seeking more detail should consult Ref. 17 and the references
therein.
The "hot big bang" model is widely accepted as the standard model of the early universe. According to this idea, our universe started in a very hot, very dense state that suddenly began to expand, and the expansion is continuing today. All of space was contained in that dense point. It is not possible to observe the expansion from an outside vantagepoint and it is not correct to think of the big bang as happening at one point in space. The big bang happened everywhere at once.
During the first fraction of a second after the big bang, it is widely believed that the universe went through a brief phase of exponential expansion called inflation. [18] Baryonic matter formed in about the first second; and the nuclei of the light elements began to form (nucleosynthesis) when the universe was only several minutes old. Baryons are particles made up of three quarks; the most familiar baryons are the protons and neutrons in the nuclei of atoms. Since all of the matter that we normally encounter is made up of atoms, baryonic matter is considered to be the "ordinary" matter in the universe.
The very early universe was hot enough to keep matter ionized, so the universe was filled with nucleons and free electrons. The density of free electrons was so high that Thomson scattering effectively made the universe opaque to electromagnetic radiation. The universe remained a baryonic plasma until around 300,000 years after the big bang when the universe had expanded and cooled to approximately 3000 K. At this point, the universe was sufficiently cool that the free electrons could join with protons to form neutral hydrogen. This process is called recombination. With electrons being taken up by atoms, the density of free electrons became sufficiently low that the mean free path of the photons became much larger (on the order of the size of the universe); and light was free to propagate. The light that was freed during recombination has now cooled to a temperature of about T0 = 2.73. This light is what we observe today as the cosmic microwave background. We see the CMB as if it were coming from a spherical shell called the surface of last scattering (Fig. 3). This shell has a finite thickness because recombination occurred over a finite amount of time.
 |
Figure 3. The surface of last scattering
(SLS), the fundamental acoustic
mode, and the sound horizon (rs,
|
Today, over very large scales, the universe is homogeneous. However, as
evidenced by our own existence, and the existence of galaxies and groups
of galaxies, etc., inhomogeneities exist up to scales on the order of
100 Mpc. Theories of structure formation require that the seeds of the
structure we observe today must have been inhomogeneities in the matter
density of the early universe. These inhomogeneities would have left
their imprint in the CMB which we would observe today as temperature
anisotropies. So, in order to explain the universe in which we live,
there should be bumps in the CMB; and these bumps should occur over
angular scales that correspond to the scale of observed structure. In
1992, the COBE satellite measured temperature fluctuations
T in the CMB,
T/T ~
10-5 on a 7° angular scale
[19],
where T is the ambient temperature of the CMB. The anisotropies
detected by COBE are considered to be large-scale variations caused by
nonuniformities generated at the creation of the universe. However,
recent observations
[20] -
[22] have found
small-scale
anisotropies that correspond to the physical scale of today's observed
structure. It is believed that these latter anisotropies are the result
of quantum fluctuations in density that existed prior to inflation which
were greatly amplified during inflation. These amplified fluctuations
became the intrinsic density perturbations which are the seeds of
structure formation.
The small-scale anisotropies in the CMB can be separated into two categories: primary and secondary. Primary anisotropies are due to effects that occur at the time of recombination and are "imprinted" in the CMB as the photons leave the surface of last scattering. Secondary anisotropies arise through scattering along the line of sight between the surface of last scattering and the observer. In this paper, we will only be concerned with the primary anisotropies. There are three main sources for primary anisotropies in the microwave background. These are the Sachs-Wolfe effect, intrinsic (adiabatic) perturbations, and a Doppler effect.
For the largest of these primary anisotropies the dominant mechanism is
the Sachs-Wolfe effect. At the surface of last scattering, matter
density fluctuations will lead to perturbations in the gravitational
potential,
. These
perturbations cause a gravitational redshift
of the photons coming from the surface of last scattering as they "climb
out" of the potential wells. This effect is described by,
T/T =
/
c2. These same perturbations in the gravitational
potential
also cause a time dilation at the surface of last scattering, so these
photons appear to come from a younger, hotter universe. This effect is
described by,
T/T =
-2(
) /
3c2. Combining these two
processes gives the Sachs-Wolfe effect
[23],
 |
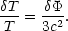(41) |
On intermediate scales, the main effect is due to adiabatic perturbations. Recombination occurs later in regions of higher density, so photons emanating from overly dense regions experience a smaller redshift from the universal expansion and thus appear hotter. The observed temperature anisotropy resulting from this process is given by [23],
 |
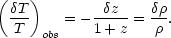(42) |
Finally, on smaller scales there is a Doppler effect that becomes important. This effect arises because the photons are last scattered in a moving plasma. The temperature anisotropy corresponding to this effect is described by [23],
 |
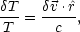(43) |
where 
denotes the
direction along the line of sight and
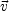is a
characteristic velocity of the material in the scattering medium.
s). The
photons of the CMB
underwent Thomson scattering in the early universe and acoustic
oscillation left their imprint at recombination.