The Dynamical Parameters of the Universe - M. Roos & S. M. Harun-or-Rashid

5. SUPERNOVA Ia CONSTRAINTS

In Section 3 we already mentioned briefly the physics of supernovæ. The SN Ia observations by the High-z Supernova Search Team (HSST) [10] and the Supernova Cosmology Project (SCP) [11] are well enough known not to require a detailed presentation here. The importance of these observations lies in that they determine approximately the linear combination Omega - Omega _m which is orthogonal to Omega ₀ = Omega _m + Omega , see Figure 1.

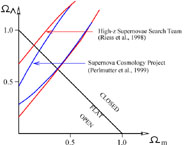Figure 1. The best fit confidence regions in ( Omega _m - Omega ) plane in the analyses of the Supernova Cosmology Project (blue curves) [11] and the High Redshift Supernova Search Team (red curves) [10]. The diagonal line corresponds to a flat cosmology. Above the flat line the Universe is closed and below it is open.

HSST use two quite distinct methods of light-curve fitting to determine the distance moduli of their 16 SNe Ia studied. Their luminosity distances are used to place constraints on six cosmological parameters: h, _m, , q₀, and the dynamical age of the Universe, t₀. The MLCS method involves statistical methods at a more refined level than the empirical template model. The distance moduli are found from a ² analysis using an empirical model containing four free parameters. The MLCS method and the template method give moduli which differ by about 1. Once the distance moduli are known, the parameters h, _m, are determined by a maximum likelihood fit, and finally the Hubble parameter is integrated out. (The results are really independent of h.) One may perhaps be somewhat concerned about the assumption that each modulus is normally distributed. We have no reason to doubt that, but if the iterative ² analysis has yielded systematically skewed pdf's, then the maximum likelihood fit will amplify the skewness.

The authors state that "the dominant source of statistical uncertainty is the extinction measurement". The main doubt raised about the SN Ia observations is the risk that (part of) the reddening of the SNe Ia could be caused by intervening dust rather than by the cosmological expansion, as we already noted after Eq. (15). Among the possible systematic errors investigated is also that associated with extinction. No systematic error is found to be important here, but for such a small sample of SNe Ia one can expect that the selection bias might be the largest problem.

The authors do not express any view about which method should be considered more reliable, thus noting that "we must consider the difference between the cosmological constraints reached from the two fitting methods to be a systematic uncertainty". We shall come back to this question later. Here we would like to point out that if one corrects for the unphysical region Omega _m < 0 using the method of Feldman & Cousins [46], the best value and the confidence contours will be shifted slightly towards higher values of Omega ₀. This shift will be more important for the MLCS method than for the template method, because the former extends deeper into the unphysical Omega _m region.

Let us now turn to SCP, which studied 42 SNe Ia. The MLCS method described above is basically repeated, but modified in many details for which we refer the reader to the source [11]. The distance moduli are again found from a chi ² analysis using an empirical model containing four free parameters, but this model is slightly different from the HSST treatment. The parameters Omega _m and Omega are then determined by a maximum likelihood fit to four parameters, of which the parameters curly M _B (an absolute magnitude) and alpha (the slope of the width-luminosity relation) are just ancillary variables which are integrated out (h does not enter at all). The likelihood contours in ( Omega _m - Omega ) plane of both supernovæ projects (SCP and HSST) are shown in Figure 1. The authors then correct the resulting likelihood contours for the unphysical region Omega _m < 0 using the method of Feldman & Cousins [46]. Since the number of SNe Ia is here so much larger than in HSST, the effects of selection and of possible systematic errors can be investigated more thoroughly. SCP quotes a total possible systematic uncertainty to Omega _m^flat and Omega ^flat of 0.05.

If we compare the observations along the line defining a flat Universe, SCP finds Omega - Omega _m = 0.44 ± 0.085 ± 0.05, whereas HSST finds Omega - Omega _m = 0.36 ± 0.10 for the MLCS method and Omega - Omega _m = 0.68 ± 0.09 for the template method. Treating this difference as a systematic error of size ± 0.16 the combined SCP result is 0.52 ± 0.10 ± 0.16. SCP and HSST then agree within their statistical errors - how well they agree cannot be established since they are not completely independent. We choose to quote a combined HSST and SCP value

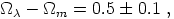(24)

which excludes a flat de Sitter universe with Omega - Omega _m = 1 by 5 sigma , and excludes a flat Einstein - de Sitter universe with Omega - Omega _m = -1 by 10 sigma .