In previous attempts to determine the luminosity function for galaxies the Virgo cluster has sometimes been included, the cluster being of a loose irregular type that possibly does not differ too much from the general field, as regards population. The distance of the cluster can be determined with a comparatively high degree of accuracy: According to the writer (1964), both redshifts and photometric data (Hubble parameter = 80) indicate an absolute modulus of 30.5; in a recent analysis of data referring to globular clusters in M87, Sandage (1968) has found a slightly larger modulus. It would naturally be of interest to compare the luminosity function of the cluster members with the general field function derived in the preceding sections.
For the brighter cluster members photometric determinations of apparent pg magnitude are available, in the first place, in Holmberg (1958) and Humason et al. (1956). For the fainter members, down to m = 15.5, magnitudes may be obtained from the comprehensive survey lists published by Zwicky and his collaborators (1961, 1963). As a first, step, the systematic errors in the Zwicky magnitude scale (Z) will be examined. Since the magnitudes have been estimated on small-scale Schraffier films, and since they have been reduced to the Shapley-Ames (1932) system, systematic deviations from the photometric lists must be expected. A plot of the magnitudes against the photometric determinations indicates that the systematic error is small at the limit Z = 15.5, also for galaxies brighter than Z = 11.5, but that in the intermediate interval the Z magnitudes are too faint by about half a magnitude. Since the systematic error presumably depends on the type and the surface magnitude of the object, and since the photometric lists in the faint magnitude classes are dominated by concentrated E and So galaxies, a more reliable result may be obtained if the statistical distribution of the uncorrected Zwicky magnitudes referring to all the galaxies in the general field (all the Zwicky survey fields outside the Virgo area) is compared with the corresponding distribution derived from photometric magnitudes. The latter may be represented by the distribution function (cf. sect. 14) that has been previously determined by the writer (1958) for general field galaxies. If the Z magnitudes are referred to the galactic pole by the Hubble (1934) absorption correction, a comparison between the two distribution curves leads to corrections to the Z magnitudes of -0.1(Z = 15.5), -0.3(Z = 15.0), -0.5(Z = 14.5), -0.6(Z = 14.0 - 12.5), and -0.4(Z = 12.0). Above the 12th magnitude, photometric results are available for practically all galaxies. It should be noted that at the fainter end of the Z scale the corrections given include a small redshift effect.
The resulting distribution of absolute pg magnitudes for Virgo cluster
members, as based on the corrected Z magnitudes and all available
photometric determinations,
is reproduced in Fig. 11. The
background-foreground field has been subtracted, as
is described below. The distribution refers to all physical members
within an elliptical area extending in right ascension from
12h08m
to 12h48m and in declination
from +2°.5 to +18°.5 (1950; cf.
Holmberg 1958)
that are included in the Zwicky survey lists (Z
15.5). The
apparent pg distance modulus has been assumed to be 30.75.
As before, the full curve refers to galaxies of all types, whereas the
broken curve represents E-So-Ir galaxies alone; the morphological types
have been estimated by the
writer on the Sky Atlas prints. For comparison, the distribution curve
for the E-So-Ir group in
Fig. 10 has been introduced as a
dotted line, adjusted to fit the cluster
frequencies in the three faintest magnitude classes. It should be noted
that the frequencies in the figure are all reduced to a class breadth of
half a magnitude.
 |
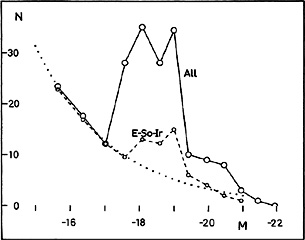Figure 11. Statistical distributions of absolute pg magnitudes of members of the Virgo cluster. For comparison, the broken curve of Fig. 10 has been reproduced as a dotted line. |
The disturbance from the background-foreground field is rather serious, especially in the fainter magnitude classes. The number of optical members in each class has been determined by means of the apparent magnitude distribution curve (general field) referred to above. The optical members have been divided into the groups E-So-Ir and Sa-Sb-Sc by means of the luminosity functions of Fig. 10, which are assumed to represent the background-foreground population; an analysis based on these curves shows that a selection by apparent magnitude would lead to a mixture of about 39 E-So-Ir and 61% Sa-Sb-Sc (constant space density).
The present investigation leads to a total number of physical cluster members of about 221 down to the limiting absolute magnitude -15.3, and a total number of optical members of about 338; the mean relative number of physical members is thus 40%. In the last magnitude class, however, the relative frequency of physical members is reduced to 14%. It may be recollected that in the satellite groups investigated this unfavorable ratio was reached first in the class centered on M = - 11.2 (cf. Table 4); in a class centered on M = - 15.5 it would be about 75%. These figures reflect the large difference in space density. Whereas the satellite groups have an average density of galaxies brighter than M = - 15.0 of about 100 per Mpc3 (cf. sect. 14), the corresponding density in the Virgo cluster, as defined here, is estimated at about 20.
The results presented in Fig. 11 show that the luminosity function for cluster members of types E-So-Ir agrees rather well with the function found for the satellite groups. The only deviation is a certain excess of cluster members in the interval M = -18 to -19.5. This hump may perhaps correspond to the secondary maximum found by Abell (1962) in the luminosity functions of several clusters; it may be noted that Abell's results refer to dense clusters, where the Sa-Sb-Sc group is practically non-existent. In the case of spiral galaxies there are interesting differences between Fig. 11 and Fig. 10. Whereas the absolute magnitudes of Sa-Sb-Sc systems in the general field extend to about M = -15, there seems to be a rather well-defined limit in the Virgo cluster close to M = - 17; beyond this magnitude there are no spiral systems at all. On the other hand, the relative number of spiral galaxies of high luminosity is about twice as high as in the general field.