


2.3. Mészáros effect
What about the case of collisionless matter in a radiation
background? The fluid treatment is not appropriate here,
since the two species of particles can interpenetrate.
A particularly interesting limit is for perturbations
well inside the horizon: the radiation can then be treated as
a smooth, unclustered background that affects only the overall
expansion rate. This is analogous to the effect of
 ,
but an analytical solution does exist in this case.
The perturbation equation is as before
,
but an analytical solution does exist in this case.
The perturbation equation is as before
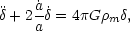 |
(30) |
but now
H2 = 8 G(
G( m +
m +  r) / 3. If we change variable to
y
r) / 3. If we change variable to
y 
 m /
m /
 r =
a / aeq, and use the Friedmann
equation, then the growth equation becomes
r =
a / aeq, and use the Friedmann
equation, then the growth equation becomes
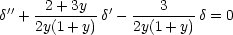 |
(31) |
(for k = 0, as appropriate for early times).
It may be seen by inspection that a growing solution exists with
 " = 0:
" = 0:
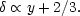 |
(32) |
It is also possible to derive the decaying mode. This is simple in
the radiation-dominated case (y << 1):

 - ln y is
easily seen to be an approximate solution in this limit.
- ln y is
easily seen to be an approximate solution in this limit.
What this says is that, at early times, the dominant energy of
radiation drives the universe to expand so fast that the matter
has no time to respond, and
 is frozen at a constant
value. At late times, the radiation becomes negligible, and the growth
increases smoothly to the Einstein-de Sitter
is frozen at a constant
value. At late times, the radiation becomes negligible, and the growth
increases smoothly to the Einstein-de Sitter

 a behaviour
(Mészáros
1974).
The overall behaviour is therefore similar to the effects of
pressure on a coupled fluid: for scales greater than the horizon,
perturbations in matter and radiation can grow together, but this
growth ceases once the perturbations enter the horizon.
However, the explanations of these two phenomena are completely
different. In the
fluid case, the radiation pressure prevents the perturbations
from collapsing further; in the collisionless case, the photons
have free-streamed away, and the matter perturbation fails to
collapse only because radiation domination ensures that the
universe expands too quickly for the matter to have time to
self-gravitate. Because matter perturbations enter the horizon (at
y = yentry) with
a behaviour
(Mészáros
1974).
The overall behaviour is therefore similar to the effects of
pressure on a coupled fluid: for scales greater than the horizon,
perturbations in matter and radiation can grow together, but this
growth ceases once the perturbations enter the horizon.
However, the explanations of these two phenomena are completely
different. In the
fluid case, the radiation pressure prevents the perturbations
from collapsing further; in the collisionless case, the photons
have free-streamed away, and the matter perturbation fails to
collapse only because radiation domination ensures that the
universe expands too quickly for the matter to have time to
self-gravitate. Because matter perturbations enter the horizon (at
y = yentry) with
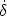 > 0,
> 0,
 is not frozen quite at
the horizon-entry
value, and continues to grow until this initial `velocity'
is redshifted away, giving a total boost factor of roughly
ln yentry. This log factor may be seen below in the
fitting formulae for the CDM power spectrum.
is not frozen quite at
the horizon-entry
value, and continues to grow until this initial `velocity'
is redshifted away, giving a total boost factor of roughly
ln yentry. This log factor may be seen below in the
fitting formulae for the CDM power spectrum.