13.3. COMPACT SOURCES

13.3.1. Self-Absorption

When the apparent source brightness temperature approaches the equivalent kinetic temperature of the relativistic electrons, synchrotron self-absorption becomes important, and part of the radiation is absorbed by the relativistic electrons along the propagation path. Below the self-absorption cutoff frequency, the spectrum is just that of a blackbody with an equivalent temperature T_k = E / k.

From Equation (1.8), E ^1/2, so in an opaque synchrotron source the flux density S ^2.5, rather than the ² law found in thermal sources. In other words, an opaque synchrotron source may be thought of as a body whose equivalent temperature depends on the square root of the frequency. Self-absorption occurs below a frequency _c where the kinetic temperature

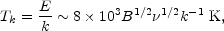is equal to the brightness temperature

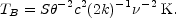Assuming uniform source parameters, the magnetic field can then be estimated from observation of _c and surface brightness from

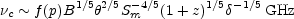(13.12)

where S_m is the maximum flux density in janskys, _c the cutoff frequency in GHz, and the angular size in milliarcseconds. The quantity is a correction for the relativistic Doppler shift if the source is moving with high velocity (see Section 13.3.7). If << c, ~ 1. The function f (p) only weakly depends on geometry and the value of p, and is about 8 for p ~ 2.5. Variations in opacity throughout the source give an overall spectrum that can be considered as the superposition of many simple regions described by Equation (13.2) and can give rise to the so-called flat or undulating spectra typically observed in compact radio sources (e.g., Condon and Dressel 1973).

The magnetic field in a compact radio source can be determined directly from the observables , S_m, and _c by Equation (13.12). The magnetic energy, E_B, can be estimated from Equation (13.8) to be

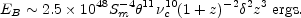(13.13)

Similarly, from Equation (13.6), the energy in relativistic electrons is given approximately by

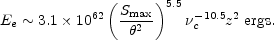(13.14)

Synchrotron radiation losses lead to a characteristic half-life at a frequency _m of

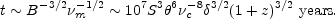(13.15)

In practice, the use of Equations (13:13) and (13.14) to derive the magnetic and particle energy is difficult due to the strong dependence on angular size and cutoff frequency. However, in almost every case where measurements exist, the particle energy appears to greatly exceed the magnetic energy. But note the dependence on and _c to about the tenth power; so small changes in the geometry may lead to other conclusions. The ratio of E_c / E_B may also be reduced considerably with even modest values of . See Section 13.3.6.