


13.3.7. Relativistic Beaming
If the source of radio emission is moving near the speed of light along
a direction which lies close to the line of sight, then the source
nearly catches up with its own
radiation. This can give the illusion of apparent transverse motion
which is greater than the speed of light. As shown in
Figure 13.8, if
the true velocity is v and is at an
angle,  , with respect to
the line of sight, then the apparent
transverse velocity, va is given by
, with respect to
the line of sight, then the apparent
transverse velocity, va is given by
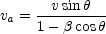 |
(13.29) |
where  =
v / c.
=
v / c.
The apparent transverse velocity has a maximum value vm ~
 c,
which occurs at an angle
c,
which occurs at an angle
 = sin-1(1 /
= sin-1(1 /
 ), where
), where
 = (1 -
= (1 -
 2)-1/2.
2)-1/2.
The Doppler shift due to the motion of the source is given by
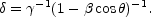 |
(13.30) |
If account is taken of the cosmological redshift, z, the total
Doppler shift is
 / (1 + z).
The observed radiation from a relativistically moving body is enhanced
by an amount
[
/ (1 + z).
The observed radiation from a relativistically moving body is enhanced
by an amount
[
 -3(1 -
-3(1 -
 cos
cos )]
)] -3,
which is often referred to as "Doppler boosting." For
-3,
which is often referred to as "Doppler boosting." For
 >>
1, the radiation is concentrated within a small cone of half-width
~ 1 /
>>
1, the radiation is concentrated within a small cone of half-width
~ 1 /  . When
. When
 ~ sin-1(1 /
~ sin-1(1 /
 ) (i.e.,
va ~ vm), then for
) (i.e.,
va ~ vm), then for
 ~ 0,
~ 0,
 ~
~
 and the
observed emission is enhanced by a factor of ~
and the
observed emission is enhanced by a factor of ~
 3.
The relation of the observed quantities va and
3.
The relation of the observed quantities va and
 and
and
 is conveniently
represented by the diagram shown in Figure 13.9.
is conveniently
represented by the diagram shown in Figure 13.9.
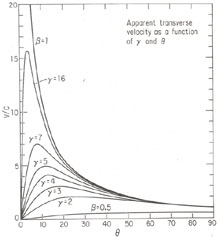 |
Figure 13.9. Apparent transverse velocity
as a function of the Lorentz factor,
|
For an approaching component viewed "head on," the boosting factor is about
8 3,
while the receding component
(cos
3,
while the receding component
(cos  ~ - 1) is
suppressed by a factor about 1/8
~ - 1) is
suppressed by a factor about 1/8
 3
and is essentially invisible. The probability that a
randomly oriented source is beamed toward the observer within an angle
3
and is essentially invisible. The probability that a
randomly oriented source is beamed toward the observer within an angle
 ~ 1 /
~ 1 /
 is ~ 1/2
is ~ 1/2
 2
for
2
for
 >> 1.
>> 1.
For values of
 ~ 7, only
about one percent of a randomly
oriented sample is expected to show superluminal motion, yet the
observed fraction is well over one-half. The large fraction of
core-dominated sources with superluminal motion
can be rationalized as the result of differential Doppler boosting which
preferentially selects sources with appropriate geometry in flux-limited
samples. Lobe-dominated
sources, on the other hand, may be assumed to be randomly oriented. But,
although the statistics are limited, superluminal motion in the central
cores of lobe-dominated sources such as 3C179
(Porcas 1981)
does not seem uncommon. It is possible that
the relativistic outflow occurs throughout a wide cone, but we see only
that portion of the cone which is moving close to the line of
sight. This would give an increased probability over the canonical 1/2
~ 7, only
about one percent of a randomly
oriented sample is expected to show superluminal motion, yet the
observed fraction is well over one-half. The large fraction of
core-dominated sources with superluminal motion
can be rationalized as the result of differential Doppler boosting which
preferentially selects sources with appropriate geometry in flux-limited
samples. Lobe-dominated
sources, on the other hand, may be assumed to be randomly oriented. But,
although the statistics are limited, superluminal motion in the central
cores of lobe-dominated sources such as 3C179
(Porcas 1981)
does not seem uncommon. It is possible that
the relativistic outflow occurs throughout a wide cone, but we see only
that portion of the cone which is moving close to the line of
sight. This would give an increased probability over the canonical 1/2
 2
of observing superluminal motion, but the good
alignment of the compact and extended jets and the highly collimated
appearance of the extended jets would appear to make this interpretation
unlikely.
2
of observing superluminal motion, but the good
alignment of the compact and extended jets and the highly collimated
appearance of the extended jets would appear to make this interpretation
unlikely.
An obvious problem with the simple relativistic beaming model is that the
observed component flux densities of superluminal sources are always
roughly comparable, whereas the expected flux density ratio of the
approaching and receding components is ~
 6.
Even if one component is stationary, the approaching
component should appear brighter by a factor of ~
6.
Even if one component is stationary, the approaching
component should appear brighter by a factor of ~
 3
unless, fortuitously, the
intrinsic component luminosities always differ by just the right amount
to cancel the differential Doppler boosting.
3
unless, fortuitously, the
intrinsic component luminosities always differ by just the right amount
to cancel the differential Doppler boosting.
This apparent conflict is resolved with the twin exhaust model of
Blandford and Konigl
(1979),
which has been the basis of most discussion of relativistic
beaming and superluminal motion. The Blandford-Konigl model postulates
symmetric relativistic beams which feed the extended lobes. The receding
beam is essentially invisible since its radiation is focused in a narrow
cone opposite to the
line of sight and is attenuated by a factor of ~ 1 / (8
 3).
Emission from the stationary core is seen at the point where
the approaching relativistic flow becomes opaque,
and so it appears to be Doppler boosted by the same amount as the
approaching components. Superluminal motion is observed between this
stationary point in the nozzle and moving shock fronts or other
inhomogeneities in the relativistic outflow. In the one source where the
appropriate measurements exist, 3C345, the core component is indeed
found to be stationary with respect to a nearby quasar
(Bartel 1986).
3).
Emission from the stationary core is seen at the point where
the approaching relativistic flow becomes opaque,
and so it appears to be Doppler boosted by the same amount as the
approaching components. Superluminal motion is observed between this
stationary point in the nozzle and moving shock fronts or other
inhomogeneities in the relativistic outflow. In the one source where the
appropriate measurements exist, 3C345, the core component is indeed
found to be stationary with respect to a nearby quasar
(Bartel 1986).
Relativistic beaming has received considerable attention because with a minimum of assumptions it provides a simple interpretation of
In view of the apparent absence of thermal plasma in compact sources
(Section 13.3.3), containing highly
relativistic electrons
( ~ 1000),
the possibility of bulk relativistic motion with
~ 1000),
the possibility of bulk relativistic motion with
 ~ 10 does
not seem unreasonable.
~ 10 does
not seem unreasonable.
Various "unified schemes" have been discussed which attempt to explain the difference between "core-dominated" (e.g., compact) and "lobe-dominated" (e.g., extended) sources (Orr and Browne 1982) or between "radio-loud" and radio-quiet quasars (Scheuer and Readhead 1979) as the effect of Doppler boosting of a randomly oriented parent population which causes a wide range in apparent core strength depending primarily on the orientation of the motion. However, as discussed in Section 13.4.1, these unified models lead to problems with understanding the extended radio structure and large-scale one-sided radio jets, as well as the optical and X-ray emission.
The correlation between the compact radio emission and X-ray (Owen et al. 1981), infrared, and optical continuum emission suggests that if the radio emission is Doppler boosted, the continuum emission throughout the spectrum may be similarly enhanced (Konigl 1981). In many ways this would be attractive since it provides a convenient interpretation of the large dispersion in the luminosity of quasars which appear to be up to about 5 magnitudes brighter than first-ranked elliptical galaxies. But if the strength of the optical continuum depends primarily on geometry, it is difficult to understand the small spread in the ratio of emission line to continuum brightness, since the line-emitting regions do not show large blue shifts (e.g., Heckman et al. 1983b).
The trivial ballistic model described above is surely too simple. If the
actual motion is in the form of a continuous flow rather than the motion
of discrete components, then the Doppler boosting factor
 =
[
=
[
 -2(1 -
-2(1 -
 2)]
2)] -2. More generally,
Lind and Blandford
(1985)
have emphasized that the actual flow velocity may
differ from the shock front velocity, which may be moving obliquely to
the main flow. Since it is the relativistic flow velocity which causes
the Doppler boosting and the shock front velocity which is seen as
superluminal motion, the apparent constraints discussed above may be
relaxed. However, in the one object where there is
a direct Doppler measure of the flow velocity, SS433 (see Chapter 9), it
is equal to the measured radio component velocity.
-2. More generally,
Lind and Blandford
(1985)
have emphasized that the actual flow velocity may
differ from the shock front velocity, which may be moving obliquely to
the main flow. Since it is the relativistic flow velocity which causes
the Doppler boosting and the shock front velocity which is seen as
superluminal motion, the apparent constraints discussed above may be
relaxed. However, in the one object where there is
a direct Doppler measure of the flow velocity, SS433 (see Chapter 9), it
is equal to the measured radio component velocity.
Realistic models will also be affected by variations in the opacity and
dispersion in the actual velocity
 and in the
intrinsic radio luminosity. Attempts to explain
the wide range of properties of compact AGNs and quasars as simply
geometric effects are probably unrealistic, but there is good evidence
that the effect of relativistic beaming is relevant to quasars and AGNs,
at least at radio wavelengths.
and in the
intrinsic radio luminosity. Attempts to explain
the wide range of properties of compact AGNs and quasars as simply
geometric effects are probably unrealistic, but there is good evidence
that the effect of relativistic beaming is relevant to quasars and AGNs,
at least at radio wavelengths.
The importance of relativistic beaming and Doppler boosting of the radio, optical, infrared, and X-ray continuum is one of the central problems of current extragalactic research and may have profound implications for our understanding of quasars and AGNs.