


The central task is for a given cosmological model, calculate the formation and evolution of a population of clusters from which synthetic X-ray and SZ catalogs can be derived. These can be used to calibrate simpler analytic models, as well as to build synthetic surveys (mock catalogs) which can be used to assess instrumental effects and survey biases. One would like to directly simulate n(M, z), n(Lx, z), n(T, z), n(Y, z) from the governing equations for collisionless and collisional matter in an expanding universe. Clearly, the quality of these statistical predictions relies on the ability to adequately resolve the internal structure and thermodynamical evolution of the ICM.
Since X-ray emission and the SZE are both consequences of hot plasma bound in the cluster's gravitational potential well, the requirements to faithfully simulate X-ray clusters and SZ clusters are essentially the same. Numerical progress can be characterized as a quest for higher resolution and essential baryonic physics. In this section I describe the technical challenges involved and the numerical methods that have been developed to overcome them. I then discuss the effects of assumed baryonic physics on ICM structure. Our point of reference is the non-radiative (so-called adiabatic) case, which has been the subject of an extensive code comparison [20].
In Norman (2003) [19] I provided a historical review of the progress that has been made in simulating the evolution of gas in galaxy clusters motivated by X-ray observations. In Norman (2004) [69] I discuss the statistical properties of simulated galaxy cluster samples and how they depend on assumed baryonic physics. The key result of this work is that while Lx is highly sensitive to input physics and numerical resolution, LSZ is not, and therefore potentially a useful proxy for the cluster mass and thereby a cosmological probe. I discuss recent progress on increasing the physics fidelity of individual cluster simulations in Sec. 5, and the use of cluster SZ surveys as cosmological probes in Sec. 6.
4.1. Dynamic range considerations
Fig. 11 illustrates the dynamic range
difficulties encountered with simulating a statistical ensemble of
galaxy clusters, while at the same time
resolving their internal structure. Massive clusters are rare at any
redshift, yet these are the ones most that are most sensitive to cosmology.
From the cluster mass function (Fig. 9),
in order to get adequate statistics, one deduces that one must simulate a
survey volume many hundreds of megaparsecs on a side
(Fig. 11, left panel).
A massive cluster has a virial radius of
~ 2 Mpc. It forms via the collapse of material within a comoving
Lagrangian volume of ~ 15 Mpc. However, tidal effects from a larger
region (50-100 Mpc) are important on the dynamics of cluster formation. The
internal structure of cluster's ICM is shown in
Fig. 11, center panel.
While clusters are
not spherical, two important radii are generally used to characterize them:
the virial radius, which is the approximate location of the virialization
shock wave that thermalizes infalling gas to 10-100 million K, and the core
radius, within which the baryon densities plateau and the highest X-ray
emissions and SZ intensity changes are measured. A typical radius is ~ 200
kpc. Within the core, radiative cooling and possibly other physical
processes are important. Outside the core, cooling times are longer than
the Hubble time, and the ICM gas is effectively adiabatic. If we wanted
to achieve
a spatial resolution of 1/10 of a core radius everywhere within the survey
volume, we would need a spatial dynamic range of D = 500 Mpc/20 kpc =
25,000. The mass dynamic range is more severe. If we want 1 million dark
matter particles within the virial radius of a 1015
M cluster, then we would need Nparticle =
Mbox / Mparticle =
cluster, then we would need Nparticle =
Mbox / Mparticle =
 m
m
 crit
L3 / 109
crit
L3 / 109
 1011 if
they were uniformly distributed in the survey volume.
1011 if
they were uniformly distributed in the survey volume.
Two solutions to spatial dynamic range problem have been developed: tree codes for gridless N-body methods [21, 22] and adaptive mesh refinement (AMR) for Eulerian particle-mesh/hydrodynamic methods [23, 24, 25, 26]. Both methods increase the spatial resolution automatically in collapsing regions as described below. The solution to the mass dynamic range problem is the use of multi-mass initial conditions in which a hierarchy of particle masses is used, with many low mass particles concentrated in the region of interest. This approach has most recently used by Springel et al. (2000) [27], who simulated the formation of a galaxy cluster dark matter halo with N = 6.9 × 106 dark matter particles, resolving the dark matter halos down to the mass scale of the Fornax dwarf spheroidal galaxy. The spatial dynamic range achieved in this simulation was R = 2 × 105. Such dynamic ranges have not yet been achieved in galaxy cluster simulations with gas.
4.2. Simulating cluster formation
Simulations of cosmological structure formation are done in a cubic domain
which is comoving with the expanding universe (cf.
Fig. 12).
Matter density and velocity
fluctuations are initialized at the starting redshift chosen such that all
modes in the volume are still in the linear regime.
Once initialized, these fluctuations are then evolved to
z = 0 by solving the equations for collisionless N-body dynamics for cold
dark matter, and the equations of ideal gas dynamics for the baryons in an
expanding universe. Making the transformation from proper to comoving
coordinates  = a(t)
= a(t)
 , Newton's laws for
the collsionless dark matter particles become
, Newton's laws for
the collsionless dark matter particles become
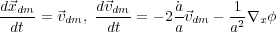 |
(34) |
where x and v are the particle's comoving position and
peculiar velocity, respectively, and
 is the
comoving gravitational potential that includes
baryonic and dark matter contributions. The hydrodynamical equations for
mass, momentum, and energy conservation in an expanding universe in
comoving coordinates are
([28])
is the
comoving gravitational potential that includes
baryonic and dark matter contributions. The hydrodynamical equations for
mass, momentum, and energy conservation in an expanding universe in
comoving coordinates are
([28])
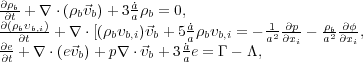 |
(35) |
where
 b,
p and e, are the baryonic
density, pressure and internal energy
density defined in the proper reference frame,
b,
p and e, are the baryonic
density, pressure and internal energy
density defined in the proper reference frame,
 b is the
comoving peculiar baryonic velocity, a = 1 / (1 + z) is
the cosmological scale
factor, and
b is the
comoving peculiar baryonic velocity, a = 1 / (1 + z) is
the cosmological scale
factor, and  and
and
 are the
microphysical heating and
cooling rates. The baryonic and dark matter components are coupled through
Poisson's equation for the gravitational potential
are the
microphysical heating and
cooling rates. The baryonic and dark matter components are coupled through
Poisson's equation for the gravitational potential
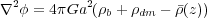 |
(36) |
where
 (z)
= 3H0
(z)
= 3H0
 m(0) /
8
m(0) /
8 Ga3 is the
proper background density of the universe.
Ga3 is the
proper background density of the universe.
The cosmological scale factor a(t) is obtained by
integrating the Friedmann equation (Eq. 4). To complete the
specification of the problem we need the ideal gas equation of state
p =
( -
1)e, and the gas heating
and cooling rates. When simulating the ICM, the simplest approximation
is to assume
-
1)e, and the gas heating
and cooling rates. When simulating the ICM, the simplest approximation
is to assume  and
and
 = 0; i.e., no
heating or cooling of the gas other than by adiabatic processes and
shock heating. Such simulations are referred to as
adiabatic (despite entropy-creating shock waves), and are a reasonable
first approximation to real clusters because
except in the cores of clusters, the radiative cooling time is longer
than a Hubble time, and gravitational heating is much larger than
sources of astrophysical heating. However, as discussed in the paper by
Cavaliere in this volume, there is strong evidence that the gas in cores
of clusters has evolved non-adiabatically. This is revealed by the
entropy profiles observed in clusters
[29]
which deviate substantially from adiabatic
predictions. In the simulations presented below, we consider radiative
cooling due to thermal bremsstrahlung, and mechanical heating due to galaxy
feedback, details of which are described below.
= 0; i.e., no
heating or cooling of the gas other than by adiabatic processes and
shock heating. Such simulations are referred to as
adiabatic (despite entropy-creating shock waves), and are a reasonable
first approximation to real clusters because
except in the cores of clusters, the radiative cooling time is longer
than a Hubble time, and gravitational heating is much larger than
sources of astrophysical heating. However, as discussed in the paper by
Cavaliere in this volume, there is strong evidence that the gas in cores
of clusters has evolved non-adiabatically. This is revealed by the
entropy profiles observed in clusters
[29]
which deviate substantially from adiabatic
predictions. In the simulations presented below, we consider radiative
cooling due to thermal bremsstrahlung, and mechanical heating due to galaxy
feedback, details of which are described below.
4.3. Numerical methods overview
A great deal of literature exists on the gravitational clustering of CDM using N-body simulations. A variety of methods have been employed including the fast grid-based methods particle-mesh (PM), and particle-particle+particle-mesh (P3M) [30], spatially adaptive methods such as adaptive P3M [31], adaptive mesh refinement [24], tree codes [32, 33], and hybrid methods such as TreePM [34]. Because of the large dynamic range required, spatially adaptive methods are favored, with Tree and TreePM methods the most widely used today. Fig. 13 shows a high resolution N-body simulation of the substructure within a dark matter halo performed by Springel using the GADGET code [78].
 |
Figure 13. Ultra-high resolution N-body simulations of the clustering of dark matter reveal a wealth of substructure. From [78]. |
When gas dynamics is included, only certain combinations of hydrodynamics algorithms and collisionless N-body algorithms are "natural". Dynamic range considerations have led to two principal approaches: P3MSPH and TreeSPH, which marries a P3M or tree code for the dark matter with the Lagrangian smoothed-particle-hydrodynamics (SPH) method [35, 21, 22], and adaptive mesh refinement (AMR), which marries PM with Eulerian finite-volume gas dynamics schemes on a spatially adaptive mesh [23, 26, 25, 36]. Pioneering hydrodynamic simulations using non-adaptive Eulerian grids [37, 38, 13] yielded some important insights about cluster formation and statistics, but generally have inadequate resolution to resolve their internal structure in large survey volumes. In the following we concentrate on our latest results using the AMR code Enzo [26]. The reader is also referred to the paper by Borgani et al. [39] which presents recent, high-resolution results from a large TreeSPH simulation.
Enzo is a grid-based hybrid code (hydro + N-body) which uses the block-structured AMR algorithm of Berger & Collela [40] to improve spatial resolution in regions of large gradients, such as in gravitationally collapsing objects. The method is attractive for cosmological applications because it: (1) is spatially- and time-adaptive, (2) uses accurate and well-tested grid-based methods for solving the hydrodynamics equations, and (3) can be well optimized and parallelized. The central idea behind AMR is to solve the evolution equations on a grid, adding finer meshes in regions that require enhanced resolution. Mesh refinement can be continued to an arbitrary level, based on criteria involving any combination of overdensity (dark matter and/or baryon), Jeans length, cooling time, etc., enabling us to tailor the adaptivity to the problem of interest. The code solves the following physics models: collisionless dark matter and star particles, using the particle-mesh N-body technique [41]; gravity, using FFTs on the root grid and multigrid relaxation on the subgrids; cosmic expansion; gas dynamics, using the piecewise parabolic method (PPM) [42]; multispecies nonequilibrium ionization and H2 chemistry, using backward Euler time differencing [28]; radiative heating and cooling, using subcycled forward Euler time differencing [43]; and a parameterized star formation/ feedback recipe [44]. At the present time, magnetic fields and radiation transport are being installed. Enzo is publicly available at http://lca.ucsd.edu/projects/enzo.
4.4. Structure of nonradiative clusters: the Santa Barbara test cluster
In Frenk et al.
[20]
12 groups compared the results of a variety of
hydrodynamic cosmological algorithms on a standard test problem. The test
problem, called the Santa Barbara cluster, was to simulate the formation
of a Coma-like cluster in a standard CDM cosmology
( m = 1)
assuming the gas is nonradiative. Groups
were provided with uniform initial conditions and were asked to carry out a
"best effort" computation, and analyze their results at z = 0.5 and z =
0 for a set of specified outputs. These outputs included global
integrated quantities,
radial profiles, and column-integrated images. The simulations varied
substantially in their spatial and mass resolution owing to algorithmic and
hardware limitations. Nonetheless, the comparisons brought out which
predicted quantities were robust, and which were not yet converged. In
Fig. 14 we show a few figures from
Frenk et al. (1999) which highlight areas of
agreement (top row) and disagreement (bottom row).
m = 1)
assuming the gas is nonradiative. Groups
were provided with uniform initial conditions and were asked to carry out a
"best effort" computation, and analyze their results at z = 0.5 and z =
0 for a set of specified outputs. These outputs included global
integrated quantities,
radial profiles, and column-integrated images. The simulations varied
substantially in their spatial and mass resolution owing to algorithmic and
hardware limitations. Nonetheless, the comparisons brought out which
predicted quantities were robust, and which were not yet converged. In
Fig. 14 we show a few figures from
Frenk et al. (1999) which highlight areas of
agreement (top row) and disagreement (bottom row).
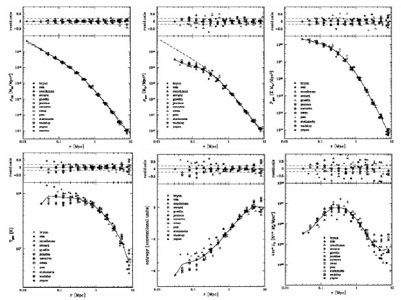 |
Figure 14. The Santa Barbara test cluster. Top row, left to right: profiles of dark matter density, gas density, and gas pressure. Bottom row, left to right: profiles of gas temperature, gas entropy, and X-ray emissivity. Different symbols correspond to different code results. From [20]. |
The top row shows profile of dark matter density, baryon density, and pressure for the different codes. All are in quite good agreement for the mechanical structure of the cluster. The dark matter profile is well described by an NFW profile which has a central cusp [45]. The baryon density profiles show more dispersion, but all codes agree that the profile flattens at small radius, as observed. All codes agree extremely well on the gas pressure profile, which is not surprising, since mechanical equilibrium is easy to achieve for all methods even with limited resolution. This bodes well for the interpretation of SZE observations of clusters, since the Compton y parameter is proportional to the projected pressure distribution. In section 5 we show results from a statistical ensemble of clusters which bear this out.
The bottom row shows the thermodynamic structure of the cluster, as well as
the profile of X-ray emissivity. The temperature profiles show a lot of
scatter within about one-third the virial radius (= 2.7 Mpc).
Systematically, the SPH codes produce nearly isothermal cores, while the
grid codes produce temperature profiles which continue to rise as
r  0.
The origin of this discrepancy has not been resolved, but
improved SPH formulations come closer to reproducing the AMR results
[51].
This discrepancy is reflected in the entropy
profiles. Again, agreement is good in the outer two-thirds of the
cluster, but the profiles show a lot of dispersion in the inner one
third. Discounting the codes
with inadequate resolution, one finds the SPH codes produce an entropy
profile which continues to fall as
r
0.
The origin of this discrepancy has not been resolved, but
improved SPH formulations come closer to reproducing the AMR results
[51].
This discrepancy is reflected in the entropy
profiles. Again, agreement is good in the outer two-thirds of the
cluster, but the profiles show a lot of dispersion in the inner one
third. Discounting the codes
with inadequate resolution, one finds the SPH codes produce an entropy
profile which continues to fall as
r  0, while the grid
codes show an entropy core, which is more consistent with observations
[29].
The dispersion in the density and temperature profiles are
amplified in the X-ray emissivity profile, since
0, while the grid
codes show an entropy core, which is more consistent with observations
[29].
The dispersion in the density and temperature profiles are
amplified in the X-ray emissivity profile, since
 x
x

 b2 T1/2. The
different codes agree on the integrated X-ray luminosity of
the cluster only to within a factor of 2. This is primarily because the
density profile is quite sensitive to resolution in the core; any
underestimate in the core density due to inadequate resolution is amplified
by the density squared dependence of the emissivity. This suggests that
quite high resolution is needed, as well as a good grasp on non-adiabatic
processes operating in cluster cores, before simulations will be able to
accurately predict X-ray luminosities.
b2 T1/2. The
different codes agree on the integrated X-ray luminosity of
the cluster only to within a factor of 2. This is primarily because the
density profile is quite sensitive to resolution in the core; any
underestimate in the core density due to inadequate resolution is amplified
by the density squared dependence of the emissivity. This suggests that
quite high resolution is needed, as well as a good grasp on non-adiabatic
processes operating in cluster cores, before simulations will be able to
accurately predict X-ray luminosities.
4.5. Effect of additional physics
Within r = 0.15 rvir, Vikhlinin et al. [50] found large variation in temperature profiles, but in all cases the gas is cooler than the cluster mean. This suggests that radiative cooling is important in cluster cores, and possibly other effects as well. It has been long known that ~ 60 percent of nearby, luminous X-ray clusters have central X-ray excesses, which has been interpreted as evidence for the presence of a cluster-wide cooling flows [64]. More recently, Ponman et al. [29] have used X-ray observations to deduce the entropy profiles in galaxy groups and clusters. They find an entropy floor in the cores of clusters indicative of extra, non-gravitational heating, which they suggest is feedback from galaxy formation. It is easy to imagine cooling and heating both may be important to the thermodynamic evolution of ICM gas.
To explore the effects of additional physics on the ICM, we recomputed the
entire sample of clusters changing the assumed baryonic physics, keeping
initial conditions the same. Three additional samples of about 100 clusters
each were simulated: The "radiative cooling" sample assumes no additional
heating, but gas is allowed to cool due to X-ray line and bremsstrahlung
emission in a 0.3 solar metallicity plasma. The "star formation" sample
uses the same cooling, but additionally cold gas is turned into
collisionless star particles at a rate
 SF =
SF =
 sf
sf
 b
/ max(
b
/ max( cool ,
cool ,
 dyn), where
dyn), where
 sf is the star formation efficiency factor ~ 0.1, and
sf is the star formation efficiency factor ~ 0.1, and
 cool and
cool and
 dyn are the local
cooling time and freefall time,
respectively. This locks up cold baryons in a non-X-ray emitting component,
which has been shown to have an important effect of the entropy profile of
the remaining hot gas
[56,
57].
Finally, we have
the "star formation feedback" sample, which is similar to the previous
sample, except that newly formed stars return a fraction of their rest mass
energy as thermal and mechanical energy. The source of this energy is high
velocity winds and supernova energy from massive stars. In Enzo,
we implement
this as thermal heating in every cell forming stars:
dyn are the local
cooling time and freefall time,
respectively. This locks up cold baryons in a non-X-ray emitting component,
which has been shown to have an important effect of the entropy profile of
the remaining hot gas
[56,
57].
Finally, we have
the "star formation feedback" sample, which is similar to the previous
sample, except that newly formed stars return a fraction of their rest mass
energy as thermal and mechanical energy. The source of this energy is high
velocity winds and supernova energy from massive stars. In Enzo,
we implement
this as thermal heating in every cell forming stars:
 sf
=
sf
=  SN
SN
 SF
c2. The feedback parameter depends on
the assumed stellar IMF the explosion energy of individual
supernovae. It is estimated to be in the range
10-6
SF
c2. The feedback parameter depends on
the assumed stellar IMF the explosion energy of individual
supernovae. It is estimated to be in the range
10-6 
 SN
SN
 10-5
[44].
We treat it as a free parameter.
10-5
[44].
We treat it as a free parameter.
Fig. 15 shows synthetic maps of X-ray surface
brightness, temperature, and
Compton y-parameter for a M = 2 × 1015
M cluster at z = 0 for the
three cases indicated. The "star formation" case is omitted because the
images are very similar to the "star formation feedback" case (see reference
[46].)
The adiabatic cluster shows that the X-ray emission is highly
concentrated to the cluster core. The projected temperature distribution
shows a lot of substructure, which is true for the adiabatic sample as a
whole
[47].
A complex virialization shock is toward the edge of the frame. The
y-parameter is smooth, relatively symmetric, and centrally
concentrated. The inclusion of radiative cooling has a strong effect on the
temperature and X-ray maps, but relatively little effect on the SZE
map. The significance of this is discussed in
Section 5. In simulations
with radiative cooling only, dense gas in merging subclusters cools to
104 K and is brought into the cluster core intact
[48].
These cold lumps
are visible as dark spots in the temperature map. They appear as X-ray
bright features. The inclusion of star formation and energy feedback erases
these cold lumps, producing maps in all three quantities that resemble
slightly smoothed versions of the adiabatic maps. However, an analysis of
the radial temperature profiles (Fig. 15)
reveal important differences in
the cluster core. The temperature continues to rise toward smaller radii in
the adiabatic case, while it plummets to ~ 104 K for the
radiative
cooling case. While the temperature profile looks qualitatively similar to
observations of so-called cooling flow clusters, our central temperature is
too low and the X-ray brightness too high. The star
formation feedback case converts the cool gas into stars, and yields a
temperature profile which follows the UTP at r
cluster at z = 0 for the
three cases indicated. The "star formation" case is omitted because the
images are very similar to the "star formation feedback" case (see reference
[46].)
The adiabatic cluster shows that the X-ray emission is highly
concentrated to the cluster core. The projected temperature distribution
shows a lot of substructure, which is true for the adiabatic sample as a
whole
[47].
A complex virialization shock is toward the edge of the frame. The
y-parameter is smooth, relatively symmetric, and centrally
concentrated. The inclusion of radiative cooling has a strong effect on the
temperature and X-ray maps, but relatively little effect on the SZE
map. The significance of this is discussed in
Section 5. In simulations
with radiative cooling only, dense gas in merging subclusters cools to
104 K and is brought into the cluster core intact
[48].
These cold lumps
are visible as dark spots in the temperature map. They appear as X-ray
bright features. The inclusion of star formation and energy feedback erases
these cold lumps, producing maps in all three quantities that resemble
slightly smoothed versions of the adiabatic maps. However, an analysis of
the radial temperature profiles (Fig. 15)
reveal important differences in
the cluster core. The temperature continues to rise toward smaller radii in
the adiabatic case, while it plummets to ~ 104 K for the
radiative
cooling case. While the temperature profile looks qualitatively similar to
observations of so-called cooling flow clusters, our central temperature is
too low and the X-ray brightness too high. The star
formation feedback case converts the cool gas into stars, and yields a
temperature profile which follows the UTP at r
 0.15rvir,
but flattens out at smaller radii. This is consistent with the high
resolution Chandra observations of Vikhlinin et al.
[50].
0.15rvir,
but flattens out at smaller radii. This is consistent with the high
resolution Chandra observations of Vikhlinin et al.
[50].
 |
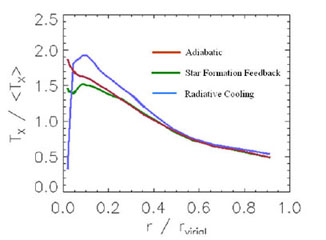 |
Figure 15. Effect of physical
processes on simulated galaxy cluster ICM observables.
Left: Columns show X-ray surface brightness, projected temperature, and
Compton y-parameter for a M = 2 × 1015
M |
|