Annu. Rev. Astron. Astrophys. 2013. 51: 207-268 Copyright © 2013 by Annual Reviews. All rights reserved

6. X_CO AT LOW METALLICITIES

CO emission is frequently very faint or nonexistent in gas-rich, actively star-forming low metallicity galaxies. This is true in absolute luminosity terms, with CO emission almost completely absent in low mass dwarf irregular galaxies below metallicity 12 + log O/H 8.0 (Elmegreen, Morris & Elmegreen 1980, Tacconi & Young 1987, Taylor, Kobulnicky & Skillman 1998). Even when it is detected, as in the case of the very nearby Small Magellanic Cloud, CO is faint (Israel et al. 1986). CO is also faint in a normalized sense. The CO-to-FIR ratios in blue, vigorously star-forming dwarf galaxies are clearly lower than in spiral galaxies (Tacconi & Young 1987, Young et al. 1996), and the same applies to other star formation rate tracers such as H (Young et al. 1996). The CO per unit starlight is also depressed in very low mass dwarfs (e.g., Young & Scoville 1991), and the ratio of CO to HI is markedly decreasing for later morphological type (Young & Knezek 1989).

Very importantly for CO emission, the low metal abundance in these systems implies lower C and O abundances and low dust-to-gas ratios (e.g., Draine et al. 2007, Muñoz-Mateos et al. 2009). Both of these factors will exert a strong effect on the relative distributions of H₂ and CO. Dust serves as the site of H₂ formation and also provides much of the far-ultraviolet shielding necessary to prevent molecules that are not strongly self-shielding, such as CO, from photodissociating. Note that galaxy mass is strongly correlated not only with metallicity, but also with a number of other parameters that may affect the equilibrium abundance of H₂, such as spiral density waves and interstellar pressure, further complicating the picture of the relation between CO luminosity and molecular mass. The critical question is whether low CO luminosities indicate a true deficit of H₂, or merely the suppression of CO emission in low metallicity environments.

Theoretical considerations, described below, lead us to expect a change in X_CO at low metallicities. Several strong lines of observational evidence, described in Section 5, also suggest that X_CO increases sharply in irregular, low-metallicity systems. Dust-based X_CO estimates, which are sensitive to the total gas present, return high values in such targets. The [CII]-to-CO ratio seems dramatically higher in dwarf irregular galaxies than in spiral galaxies, supporting the hypothesis of a reservoir of H₂ at low A_V where most carbon is locked in [CII] rather than CO. The SFR-to-CO ratio also increases, offering circumstantial evidence for star-forming gas not traced by CO.

6.1. Theoretical Expectations for Low Metallicity Gas

Naively, one would expect that a lower C and O would imply consequently fainter CO emission. Because CO is optically thick, however, its luminosity is determined by the emitting area and its brightness temperature and velocity spread. The dependence of X_CO on metallicity hinges fundamentally on how the relative sizes of the [CII] and CO-emitting regions change with lower heavy element and dust abundance (Fig. 8, see the discussion of cloud structure in Section 2.5). Maloney & Black (1988) carried out one of the first thorough analyses of the problem. Here we note the physical drivers for the location of bright CO emission and then discuss the implications for low metallicity.

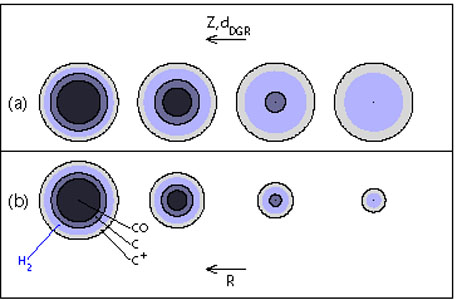Figure 8. Effect of metallicity on CO and H2 in a spherical clump immersed in a uniform radiation field. Blue shading indicates the region where the gas is molecular, according to Eq. 25. Increasingly darker shading shows the regions where carbon is found as C+, C, or CO. The top sequence (a) illustrates the effect of decreasing metallicity and dust-to-gas ratio on the distribution of C+, CO, and H2. Mostly because of the increase in NH required to attain a given AV, the CO emitting region is pushed further into the clump until, for a fixed cloud size, it disappears at low enough metallicities. The bottom sequence (b) illustrates the effect of changing the clump size or column density at a fixed metallicity (adapted from Bolatto, Jackson & Ingalls 1999, Wolfire, Hollenbach & McKee 2010).

The relative distributions of CO and H₂ will be a detailed function of the balance of formation and destruction of CO, processes discussed for diffuse and dense material by van Dishoeck & Black (1986), van Dishoeck & Black (1988) (see also Wolfire, Hollenbach & McKee 2010, appendices B and C). CO formation proceeds mainly through the production of OH via ion-neutral reactions initiated by cosmic-ray ionization. Once OH is formed the chemistry proceeds via ion-neutral reactions to form HCO⁺ followed by the dissociative recombination of HCO⁺ to form CO. The formation rates of CO thus depend on the abundance of C times the abundance of O. Because the rate of formation depends on the abundance of OH, the rate of destruction of OH by far-ultraviolet photons represents an additional limiting factor in setting the CO abundance (e.g., Wolfire, Hollenbach & McKee 2010, Appendix C).

At depths where the CO line originates the destruction of CO proceeds mainly via photodissociation by far-ultraviolet radiation. These dissociations occur via line transitions between the ground state and predissociated excited electronic states. That is, the majority of the transitions to these excited electronic states result in dissociation rather than CO in bound, excited levels. The longest wavelength dissociating transition lies at 1076 Å. Thus the dissociation of CO in the ISM occurs in the narrow far-ultraviolet band between 1076 Å and the Lyman limit at 912 Å. These dissociation bands for CO overlap the Lyman bands of H₂, and the Lyman lines of HI. Thus HI and H₂ can shield CO. Because CO dissociates in line transitions, similar to H₂, it can also self-shield at sufficiently large CO column densities. In addition to gas opacity, dust absorption and scattering will attenuate the dissociating radiation field.

A simple expression illustrates the dependence of the CO dissociation rate on these various process: R = R₀ exp(- A_V) s^-1. The first two factors reflect the incident radiation field. R₀ is the dissociation rate in free space for a radiation field with a particular shape and is a scaling factor that measures the strength of the radiation field. The exponential factor reflects shielding by dust, with A_V the line of sight extinction into the cloud. The factor includes both cloud geometry and the translation from A_V into extinction at the dissociating wavelengths, accounting for absorption and scattering by grains in the far-ultraviolet. The parameter accounts for shielding by HI and H₂ gas and CO self-shielding.

For a Draine (1978) interstellar radiation field, R₀ = 2.6 × 10^-10 s^-1 (Visser et al. 2009); R₀ will vary for radiation fields with other shapes. For typical ISM grains and penetration into a plane parallel layer, = 3.53 (van Dishoeck, Jonkheid & van Hemert 2006). The parameter is a monotonically decreasing function of the HI, H₂, and CO column densities and varies between 1 (for no shielding) and 0. A fit to the line overlap and self-shielding function, , can be found in Visser et al. (2009).

Balancing CO formation and destruction Wolfire, Hollenbach & McKee (2010) find an expression for the depth into a cloud at which _CO = 1 for the J = 1 → 0 transition:

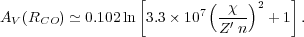(24)

Here n is the gas density and and Z' are the far-ultraviolet field and gas phase abundances in units of the local Galactic values. A_V(R_CO ) is the depth in units of magnitudes of visual extinction due to dust at which _CO = 1. In this expression the explicit dependence on dust-to-gas ratio cancels out, but the conversion from A_V to column density will depend on the dust-to-gas ratio.

Variations in X_CO will depend on the relative extent of the CO and H₂ layers. Therefore, Wolfire, Hollenbach & McKee (2010) present a similar expression for the depth at which the gas is half molecular

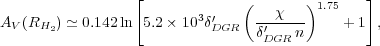(25)

where _DGR' is the dust-to-gas ratio relative to the local Galactic value.

The difference between the depth of the H₂ and CO layers is thus: A_V = 0.53 - 0.045 ln / n + 0.107 ln(_DGR') - 0.204 ln(Z'). For a dust-to-gas ratio that scales as the gas phase metallicity we have

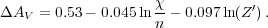(26)

The equations for A_V(R_CO), A_V(R_H2), and A_V all show weak dependencies on , _DGR', and Z'. Thus they may be expected to change only weakly with changing local conditions and at lower metallicity, the location of the _CO = 1 surface, the H₂ transition, and the spacing between the two all remain approximately fixed in units of visual extinction due to dust. The ratio of dust to gas also drop with metallicity (Draine et al. 2007). As a consequence of lower dust abundance and approximately constant A_V, the physical depth of the _CO = 1 surface shifts deeper into the cloud, producing a larger surface layer of H₂ at low A_V. A correspondingly larger layer of HI also exists beyond A_V(R_H2) but does not bear directly on this review. Thus, with lower metallicity and correspondingly lower dust abundance, CO retreats further into the cloud than H₂. Figure 8 illustrates the expected interplay of HI, H₂, CO, and C⁺ in a spherical cloud and the impact of changing metallicity (top row) and cloud size or column density (bottom row).

If M(R_H2) is the molecular mass within the radius where the molecular fraction is 0.5, and M(CO) is the mass within the radius of the _CO = 1 surface, then the "CO-faint" gas fraction can be defined as f = [M(R_H2) - M(R_CO)] / M(R_H2)]. For a cloud with an r^-1 density profile, corresponding to M(r) r², the "CO-faint" gas mass fraction is given by

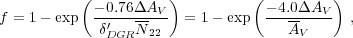(27)

where A_V is the optical depth in the "CO-faint" gas layer (Eq. 26), N₂₂ is the mean H column density in the CO portion of the cloud in units of 10²² cm^-2, and A_V = 5.26 '_DGR N₂₂.

The retreat of the CO emitting surface was first noted by early studies (Maloney & Black 1988, Lequeux et al. 1994). This shrinking CO core leads to lower beam filling factors, and thus a lower observed CO intensity (e.g., Pak et al. 1998, Bolatto, Jackson & Ingalls 1999). The result is that X_CO increases with decreasing metal abundance. Maloney & Black (1988) find nearly equal CO and H₂ cloud sizes at solar metallicity and so note that increasing CO abundance above solar will not substantially change X_CO. Recent observational estimates find the fraction of "CO-faint" molecular gas mass to be ~ 50% in the Milky Way (see Section 4.2.4). This allows slightly more room for a changing X_CO moving to supersolar metallicities. For example, a change from X_CO,20 2 to ~ 1.3 might be plausible due to the effect of increasing metallicity.

A secondary consideration is that the brightness temperature of CO may also be affected by systematic excitation changes with metallicity. The temperature of the gas represents a balance between heating and cooling. If grain photoelectric heating dominates at the _CO = 1 surface, then to first order both the heating rate (proportional to the dust-to-gas ratio for photoelectric heating) and the cooling rate (proportional to metal abundance for line cooling) will scale similarly with metallicity, yielding no change in gas temperature with metal abundance. It remains unclear, however, whether the photoelectric heating efficiency increases, decreases, or stays the same at low metallicities (e.g., Röllig et al. 2006, Israel & Maloney 2011).

In summary, models predict an increase in X_CO for large regions of low metallicity galaxies due to the contraction of the CO-emitting surface relative to the area where the gas is H₂ for a fixed cloud size. This effect may be offset (or compounded) by a mild increase (or decrease) in brightness temperature brought about by changes in heating sources, chiefly the photoelectric heating effect. Note that the usefulness of CO as a tracer of total H₂ mass will ultimately break down at low enough metallicity, where it will be found only at the highest column densities and in well-shielded environments.

6.2. Metallicity-Dependent Calibrations of X_CO

Calibrating X_CO as a function of metallicity has represented a key goal of extragalactic CO studies for two decades. The issue remains complicated for several reasons: some practical, some theoretical. We have already discussed the biases and caveats of the different X_CO extragalactic estimators. On practical grounds, the faintness of CO in low luminosity, low metallicity systems renders observations very difficult. The abscissa in any calibration, metallicity, also remains one of the hardest quantities in extragalactic astronomy to measure with precision. The basic cloud structure arguments presented in Section 6.1 suggest that the sub- and supersolar regimes should be treated differently — or at least that a single power law represents a poor choice across all regimes. We will discuss here several existing calibrations of X_CO with metallicity and contrast them against the data, presenting a simple tentative formula that includes metallicity effects in Section 9.

Some of the most comprehensive and widely used work comparing X_CO to metallicity relies mostly on virial mass-based X_CO estimates (e.g., Wilson 1995, Arimoto, Sofue & Tsujimoto 1996, Boselli, Lequeux & Gavazzi 2002, Bolatto et al. 2008). These calibrations should best be viewed as calibrations of X_CO within the CO-emitting region, and not be used to predict the total H₂ content from CO on large scales. We suggest that the lack of an X_CO vs. metallicity trend in Bolatto et al. (2008) and the weak trend in Wilson (1995) reflect the uniformity of opaque, bright CO-emitting structures across many types of galaxies. Similarly, the calibrations by Arimoto, Sofue & Tsujimoto (1996) and Boselli, Lequeux & Gavazzi (2002) rely on virial masses to derive X_CO as a function of metallicity (and so do Obreschkow & Rawlings 2009).

What are the appropriate calibrations to consider for X_CO as a function of metallicity? Dust-based approaches such as Israel (1997) or the "alternative approach" of Boselli, Lequeux & Gavazzi (2002) or combined CO, [CII], and dust modeling (Madden et al. 1997, Pak et al. 1998) appear to offer the best, or at least the most accessible, extragalactic approach. These have the potential to capture the whole H₂ distribution. In the following pagraphs we employ these observations to test recent theoretical work on the subject (e.g., Wolfire, Hollenbach & McKee 2010, Glover et al. 2010, Narayanan et al. 2012, Feldmann, Gnedin & Kravtsov 2012). Note that, as discussed in Section 6.1, we do not expect X_CO to change significantly due to metallicity in the supersolar metallicity regime. Instead, variations due to optical depth, line width, or excitation temperature are likely to dominate.

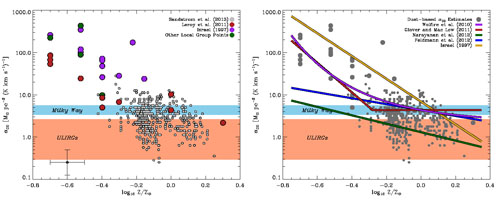Figure 9. Conversion factor, estimated from dust-based approaches, as a function of gas-phase abundance. (Left) Color points show estimates for very nearby galaxies Israel (1997), Madden et al. (1997, based on [CII]), Leroy et al. (2007), Gratier et al. (2010), Roman-Duval et al. (2010), Leroy et al. (2011), Bolatto et al. (2011), and Smith et al. (2012). Gray points show high quality solutions from analysis of 22 nearby disk galaxies by Sandstrom et al. (2012), with typical uncertainties illustrated by the error bars near the bottom left corner. Metallicities are from Israel (1997), Bolatto et al. (2008), and Moustakas et al. (2010) and quoted relative to solar in the relevant system (12 + log[O/H] = 8.7 for the first two, 12 + log[O/H] = 8.5 for the latter which uses the metallicity calibration by Pilyugin & Thuan 2005). Note that significant systematic uncertainty is associated with the x-axis. The color bands illustrate our recommended ranges in CO for the Milky Way and ULIRGs. (Right) Colored lines indicate predictions for XCO as a function of metallicity from the references indicated, normalized to XCO,20 = 2 at solar metallicity where necessary. For these predictions, we assume that GMCs have <GMC> = 100 M pc-2, which we translate to a mean extinction through the cloud using Eq. 21. Dust-based determinations find a sharp increase in XCO with decreasing metallicity below Z ~ 1/3 - 1/2 Z.

Figure 9 presents an attempt at such a comparison. We show an ensemble of dust and FIR determinations (Israel 1997, Madden et al. 1997, Leroy et al. 2007, Gratier et al. 2010, Leroy et al. 2011, Bolatto et al. 2011, Smith et al. 2012) targeting local galaxies along with X_CO estimates determined (Sandstrom et al. 2012) for a sample of 22 nearby disk galaxies. In the right panel we plot theoretical predictions for X_CO as a function of metal abundance, assuming dust-to-gas ratio is linearly dependent on metallicity. For Wolfire, Hollenbach & McKee (2010) we plot the equation

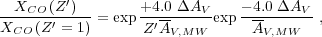(28)

which is obtained from Eq. 27 assuming that dust-to-gas ratio tracks metallicity. Here Z' is the abundance of heavy elements and dust relative to solar, X_CO (Z' = 1) is the CO-to-H₂ conversion factor at solar metallicity, and A_V,MW is the mean extinction through a GMC at Milky Way metallicity (A_V,MW 5 for _GMC 100 Mpc^-2). The prediction for Glover & Mac Low (2011) simply adapts their Equation 16, which gives X_CO as a function of A_V. We assume that the mean extinction through a cloud scales as the metal abundance, A_V = Z' A_V,MW

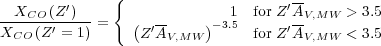(29)

In the full prediction of Narayanan et al. (2012), X_CO depends on a combination of I_CO and Z, rather than metallicity alone. We cannot readily place their predictions in this plot. Instead we plot their Equation 6, in which X_CO depends on Z' and _H2. For each of these predictions, we assume _H2 = 100 M pc^-2, translating this to A_V,0 assuming R_V = 3.1 and the dust-to-gas ratio of Bohlin, Savage & Drake (1978). We also plot the metallicity-only fit by (note that his fit includes the radiation field, with a definition that renders it heavily degenerate with the dust-to-gas ratio, Israel 1997).

Figure 9 shows large scatter, even among determinations using similar techniques for the same galaxy, but provides reasonable evidence for an upturn in X_CO with decreasing metallicity below Z' ~ 1/3 - 1/2. The fit by Israel (1997) skirts the upper envelope of measured values, while the prediction by Feldmann, Gnedin & Kravtsov (2012) predicts weaker-than-observed variations at very low Z', though data remain scarce (those points represent only ~ 4 galaxies). The sharp nonlinear increases predicted by shielding-oriented models like Wolfire, Hollenbach & McKee (2010) or the simulations of Glover & Mac Low (2011) provide the best fits to the existing data.

Less direct approaches to constrain X_CO also exist. A recently popular technique is to assume an underlying relationship between star formation and molecular gas and to use this relationship and an estimate of the recent star formation rate to arrive at the H₂ present. Schruba et al. (2012) applied this technique to estimate X_CO as function of metallicity in a sample of nearby galaxies. Genzel et al. (2012) combined a wide set of low and high redshift measurements to estimate the dependence of X_CO on metallicity. Both studies find a significant dependence of X_CO on metallicity but with a wide range of possible power law exponents, X_CO Z¹ to Z³. The strength of this approach is that the observations needed to make such estimates are widely accessible. The weakness, of course, is that it requires assuming an underlying relationship between H₂ and star formation. Any true dependence of the star formation efficiency on metallicity, or any other quantity covariant with metallicity, will be recast as additional variations in X_CO.

If X_CO does increase rapidly moving to low metallicity, our knowledge of the distribution function of molecular column density will present a practical limit to the usefulness of CO to trace H₂. At metallicities perhaps as high one half solar, half of the H₂ mass will exist outside the CO-emitting surface, and that fraction will rapidly increase for decreasing metallicity. Thus, application of a CO-to-H₂ conversion factor at very low metallicity ultimately involves extrapolating the total mass of a cloud from only a small inner part; by Z' ~ 0.1 this may already be analogous to measuring the total H₂ mass of a Milky Way cloud from HCN emission or some other high density tracer. In the Milky Way, the fraction of cloud mass in high column density lines of sight can vary dramatically from cloud to cloud (e.g., Kainulainen et al. 2009, Lada, Lombardi & Alves 2010). In the LMC, Israel et al. (1996) found large region-to-region variations in the [CII]-to-CO ratio. As one moves to increasingly low metallicities, the use of CO emission to quantify the H₂ reservoir becomes more and more extrapolative. While difficult to quantify, this effect should add significant scatter that increases with decreasing metallicity, and will eventually present a practical floor past which CO is not a useful tracer of total H₂ mass.