Copyright © 2017 by Annual Reviews. All rights reserved
| Annu. Rev. Astron. Astrophys. 2017. 55: 59-109
Copyright © 2017 by Annual Reviews. All rights reserved |
1.1. What do we want to learn?
Do we understand galaxy formation? Galaxies have been called the building blocks of the Universe and they are clearly the fundamental units within which stars are organized. They do show characteristic sizes (Rgal ∼ kpc) and masses (Mgal ∼ 1010 M⊙). Their abundance (∼ 10−2 Mpc−3) is set by their characteristic mass and the fact that they constitute a moderate fraction (fgal ∼ 10 %) of the cosmic baryon budget. Can we derive these numbers (Rgal, Mgal, fgal) from first principles? Can we, from straightforward numerical simulations, chart the history of when, where and how the formation and evolution of galaxies occurred? And, finally, do we understand it all well enough to characterize the internal properties of these systems, their ages, kinematics and mass distributions and their organization into families having properties describable using relatively few parameters?
As a problem in physics, there are four clearly definable aspects: (1) specification of the initial conditions; (2) knowledge of the physical processes primarily responsible for understanding each phase of galactic evolution; (3) computational tools that permit us to start with (1), utilize (2) to construct models predicting the detailed properties of representative samples of galaxies to be (4) tested by direct comparison with the rich treasury of information provided by nature revealed by modern observational technology.
We will argue that the current, standard cosmological models are sufficiently accurate to provide initial conditions as required to any specified accuracy. With regard to physical processes, the problem is divided into two parts: (A) what would the evolution be if we only had to consider dark matter; and (B) how is the picture altered if we include the primordial radiation fields, the baryonic gas as well as the energy, processed interstellar matter and momentum input from the stars and massive black holes? The current state of the art shows a good grasp of problem (A) - different investigators using different codes recover quite similar descriptions of the universe; but with regard to the more complex problem (B) - allowing for 'feedback' from stars and black holes, we have only preliminary gropings toward physical understanding. One simple example suffices. The non-thermal and relativistic components of the interstellar medium - magnetic fields and cosmic rays - are not thought to be primordial but in our Galaxy have energy densities comparable with kinetic energy densities, significantly higher than thermal energy densities (e.g. Boulares & Cox 1990, Ferrière 2001). Are these components essential to understanding galaxy formation or are the mere byproducts? They are not included in most treatments, and the omission may (or may not) be crucial. However, the situation is improving.
As a result of our success with regard to problem (A) - the 'stage setting' so to speak - we have a moderately good grasp of the physics that determines the approximate values of the three scales, the numbers for size, mass and abundance, noted as the fundamental characteristics of galaxies, but we have a poor knowledge of the details that are important in determining the internal structure and evolution of these systems. Finally, our computational tools are marginally adequate for the simpler part (A) of the task, but perhaps not up to the challenge of the multi-dimensional, multi-component, time-dependent computation involving the necessary range of temporal and spatial scales.
So far we have been describing this as an ab initio problem of physics, like the motion of a playground swing - though more complex - but of course this is not the way that the history unfolded. Observational discoveries have guided us every step of the way, often pointing out to us how much too simple our models have been. These observations have been of two kinds, those that describe the Universe as it is (e.g. galaxy rotation curves or the details of the multi-phase interstellar medium) and those that tell us of the time development, either through using the archaeological method of examining the stellar populations of nearby galaxies and determining when/how the various components were assembled, or by using the Universe as a time machine and looking at the progenitor populations at earlier cosmic epochs. In any case, direct observations are the facts that all models have to be tested against and in most cases they are the drivers for progress in theoretical galaxy formation, both on the small scales of individual galaxies as well as on the large scale distribution and redshift evolution of galaxy populations.
Galaxy formation has become such a large field in astrophysics that a full overview of all theoretical challenges is beyond the scope of a single review. Here we focus on a subset of problems in computational astrophysics. Numerical implementations of 'feedback' processes have traditionally been tested with idealised galaxy models and merger simulations. These models have resulted in important insights on star formation, morphological and kinematic transformations, merger driven gas flows, triggering of star formation, the impact of accreting black holes on the termination of star formation, and size evolution. We give an overview of these feedback models and their use in modern cosmological simulations of galaxy formation. We briefly highlight major steps forward like the successful simulation of spiral galaxies and the cosmological evolution of galaxy populations. Some other major theoretical challenges that can be addressed with cosmological galaxy formation simulations are not discussed here in detail. One of these is how galaxies accrete their gas. Gas accretion is a necessary and fundamental process for galaxy formation but surprisingly it has not yet been conclusively observed. From numerical studies it is still unclear whether the gas is accreted onto the galaxies cold filaments (Kereš et al. 2005, Dekel et al. 2009) or whether the filaments dissolve in the halos and accretion is more smooth (Nelson et al. 2013). A related question is how galactic outflows actually transport metal enriched material into the circumgalactic medium (see e.g. Oppenheimer & Davé 2006, Schaye et al. 2015). This is also a numerically challenging question, as the spatial resolution in the halos of galaxies is typically much lower than in the dense regions and mixing processes are highly complex (e.g. Scannapieco & Brüggen 2015). We also do not address issues that test galaxy formation on small scales in the context of the underlying cold dark matter cosmological model like the 'Too big to fail' problem (Boylan-Kolchin, Bullock & Kaplinghat 2011) or the question whether small dark matter halos have cusps or cores (e.g. Kravtsov et al. 1998, Pontzen & Governato 2012). We accept the standard cold dark matter paradigm because of its numerous proven successes on large scales, while fully aware of the challenges it faces on small scales. Instead we focus on the physics of the interstellar medium (ISM). The ISM strongly influences galaxy formation. Many processes determining star formation and galactic outflows as well major observable features act in the ISM and a better understanding and more accurate modelling of theses processes are, in our view, the major theoretical challenge for galaxy formation in the future.
1.2. Some relevant observations
Our summary of observations that put important constraints on theoretical galaxy formation models will necessarily be brief and does not attempt to provide a full list of references. The first and most obvious is the observational information accumulated in the last century specifying the four principle components of all massive galaxies; stars, gas, dark matter and super-massive black holes:
1.2.1. Sstars From Hubble's time onwards we realized that the bulk of the mass in the visible parts of galaxies resides in one of two components, a spheroidal part having a scale length typically of only a few kpc to a few tens of kpc with a roughly de Vaucouleurs surface density profile (de Vaucouleurs 1948) and a flattened, rotationally supported disk/spiral component, which is typically somewhat larger (apart from the highest mass systems) and has a roughly exponential profile (e.g. Shen et al. 2003, Blanton & Moustakas 2009, van der Kruit & Freeman 2011). These two components appear to be distinct, and environmental considerations must be important in understanding their formation, since isolated systems tend to be disk dominated and those in regions of high galactic density tend to be dominated by the spheroidal component (e.g. Dressler 1980, Blanton & Moustakas 2009, Kormendy et al. 2010, Cappellari 2011). Recent integral field studies have significantly improved our understanding of the complex kinematics of galaxies (de Zeeuw et al. 2002, Cappellari et al. 2011, Sánchez et al. 2012, Fogarty et al. 2014, Bundy et al. 2015). Stellar dating indicates extended and relatively flat star formation histories for the disks with typical ages of a few billion years and peaked star formation histories with typical stellar ages of ∼ 10 billion years for massive early type galaxies (e.g. Kauffmann et al. 2003, Heavens et al. 2004, Thomas et al. 2005, Renzini 2006, Kormendy et al. 2009). Large surveys made it possible to observe relatively accurate stellar mass functions not only in the local Universe (e.g. Pérez-González et al. 2008, Li & White 2009, Bernardi et al. 2013) but also towards higher redshifts (e.g. Bouwens et al. 2012, Moustakas et al. 2013, Muzzin et al. 2013, Duncan et al. 2014, Song et al. 2016).
1.2.2. Gas Typical Milky Way like spiral galaxies roughly have ∼ 10% of their mass in cold interstellar medium gas (≲ 104 K). An even larger fraction (some of it hotter and ionised) gas might be stored in the so called 'circum galacitc medium', the region extending from the star-forming interstellar medium into the galaxies halos (e.g. Werk et al. 2014, Somerville & Davé 2015). More massive early-type galaxies typically have significantly lower cold gas fractions, although they are not devoid of cold gas, contrary to the traditional picture (Saintonge et al. 2011, Catinella et al. 2010, Young et al. 2011, Serra et al. 2012). Massive early-type systems are usually embedded in hot (> 105 K) X-ray emitting gas comprising a significant fraction of the total baryonic mass (e.g. Mulchaey 2000, Vikhlinin et al. 2006, Sun et al. 2009, Giodini et al. 2009, Dai et al. 2010, Kravtsov & Borgani 2012, Renzini & Andreon 2014, Anderson et al. 2015).
1.2.3. Dark matter Following Zwicky's and Babcock's work in the 1930s and then the work of many authors on the rotation curves of normal galaxies in the 1970s and 1980s (e.g. Sofue & Rubin 2001), it became apparent that the stars in most normal galaxies are embedded in massive halos comprised of some unknown type of dark matter with a total mass and size roughly 10 times that of the stellar component. The generally flat observed rotation curves of spiral galaxies are an important test for cosmological formation models (see Courteau et al. 2014). Recent result from strong lensing have contributed to our knowledge of the dark matter content of massive galaxies, which have typical contributions of 5% to 20% within their stellar half-light radii (e.g. Koopmans et al. 2009, Treu 2010, see also lensing measurements of the stellar-to-halo mass ratio, Mandelbaum et al. 2006). Dwarf galaxies like Sculptor or Fornax or the recently discovered category of large utradiffuse galaxies (c.f. van Dokkum et al. 2015) are dominated by dark matter throughout (see also Kormendy & Freeman 2016).
1.2.4. Super-massive black holes A number of studies have indicated that super massive black holes typically reside in the centers of normal galaxies (having stellar masses ≳ 1010.3 M⊙), with their masses tightly correlated with the masses (and stellar velocity dispersions) of the spheroidal components of the galaxies, the ratio being roughly 5:1000 (see e.g. Genzel et al. 1997, Kormendy & Ho 2013 for a review). Given the evident association with AGN, it is widely believed that the energy emitted by these monsters during their formation is roughly 10% of their rest mass (Shakura & Sunyaev 1973, Soltan 1982), that makes them competitive with high mass stars with regard to energy input (in various forms) into the surrounding galaxies (e.g. Silk & Rees 1998).
1.2.5. The Milky Way The archaeological method was used very successfully in the last half of the 20th century to reconstruct a plausible history of our own galaxy, the Milky Way. The Sun is a typical star in the disk component that gradually formed from relatively metal rich gas. It appears that this disk component grew slowly, in size and mass, as rotationally supported gas was steadily turned into stars over cosmic time, and the typical stars in our cosmic neighborhood were formed only 3-6 billion years ago, relatively late in the evolution of the Universe. The fact that much less than 10% of the disk stellar mass has a metallicity that is less than 10% of the latest formed stars tells one immediately that the disk is temporally a 'secondary' structure heavily contaminated by the metal rich ejecta from earlier stellar generations (Ostriker & Thuan 1975). The age distribution tells us that it formed 'inside-out' with the stars in the low metallicity, gas rich outer parts of the disk formed most recently (see e.g. Rix & Bovy 2013). The somewhat tri-axial, bar-like, inner structure is old and may have formed via the instability of a cold rotating disk (e.g. Ostriker & Peebles 1973), but the outer spheroidal halo, is likely the debris from in-falling, captured, smaller systems that has accumulated over time. The stars in this extended spheroidal (or elliptical) component are typically ∼ 10 billion years old, are lower in heavy element abundances and tend to have an isotropic or even somewhat radially biased distribution of orbits.
Most of the stars (the fraction might be as high as ≳ 95%) in our Galaxy were made from gas that was added to the Galaxy, forming into stars within the system and only a very small fraction of the stellar mass comes from stars made in other galaxies that were added to our system via galactic mergers (Kennicutt & Evans 2012). Thus 'major mergers' might not have been at all important in the late formation history of our Galaxy, or of others with very similar structures.
Work by Eggen, Lynden-Bell & Sandage (1962) in the early 1960s provided solid evidence that our galaxy began in a phase of dramatic collapse. Other, spheroidal, systems observed in detail, while more massive and more metal rich, seemed to be composed of stars of similar age and orbital properties, so it was plausible that they formed by a similar process. In this simple picture the disk is a later addition as higher angular momentum, already contaminated material drifted into the galaxy, accumulated in a rotating disk and was gradually turned into the bulk of the stars. This provides a natural explanation for the two components of the Hubble classification and also a reason for the absence of the disk components in dense environments within which tidal or ram-pressure effects prevent the late formation of disks. While the details of this story have evolved, the overall picture has withstood the test of time remarkably well. The archaeological approach to galaxy formation and evolution continues, with much useful work being done in teasing out the details of how the extended spheroidal component was put into place. If this picture is correct, then in the much more massive elliptical galaxies like M87 the secondary, stellar component added by the cannibalization of numerous smaller systems, may comprise 20% up to 50% of the total, in contrast to the much smaller fraction of accreted stars in the common, lower mass, disk-like spiral systems.
The Milky Way also holds most information about the detailed structure of the multi-phase interstellar medium (ISM). Most of the gas is found in three phases, the cold neutral medium, the warm neutral medium and the hot ionized medium. The hot phase fills about 30% of the volume (Ferrière 2001) in the disk but dominates further than a few kpc from the disk midplane (see Kalberla & Kerp 2009, and Sec. 3).
1.3. Learning from galaxy evolution with redshift
Observations of galaxies extending towards higher redshift (and thus earlier times) have given additional insight in galaxy properties of fundamental importance.
1.3.1. Ubiquitous winds Galactic winds, with velocities up to 500 km s−1 and most likely of bi-conical nature, carrying large amounts of material out of star forming galaxies (the rate being comparable to and higher than the star formation rate) are ubiquitous, not only in the nearby Universe (e.g. Heckman, Armus & Miley 1990, Martin 1999, Heckman et al. 2000, Veilleux, Cecil & Bland-Hawthorn 2005, Rubin et al. 2014) but also at higher redshift at the cosmic peak of conversion of gas into stars (Pettini et al. 2001, Steidel et al. 2010, Shapley 2011, Martin et al. 2013). At low as well as high redshift these winds most likely enrich the circum-galactic medium with gas, metals and possibly magnetic fields (Werk et al. 2014, Steidel et al. 2010, Bernet, Miniati & Lilly 2013), providing the material which, if falling back in at later times with added angular momentum (Peebles 1969), can be the source of the secondary disk systems. These winds transport gas out of the galaxies at rates similar to which gas is converted into stars and therefore have to be of importance for regulating the formation efficiency of stars in galaxies. Even at high redshift the launching sites of star formation driven (Newman et al. 2012b) and AGN driven (Genzel et al. 2014) winds can now be resolved with modern instruments.
1.3.2. Size evolution of early-type galaxies Today's massive (∼ 1011 M⊙) early-type galaxies can form early and become 'red and dead' by z ∼ 2 as much smaller systems than those seen today (∼ 1 kpc), with the growth in size (while not forming stars) to be understood as a likely sign of subsequent addition of stars in minor mergers at larger radii (e.g. Daddi et al. 2005, Trujillo et al. 2007, van Dokkum et al. 2010, Damjanov et al. 2011). Observations of significant structural evolution of massive early-type galaxies disfavor any singular monolithic collapse or binary merger formation scenario (van Dokkum et al. 2008). Also the observed strong increase in size and the weak decrease in velocity dispersion (Cenarro & Trujillo 2009) of the early-type galaxy population as a whole, which also includes additions to the red sequence at lower redshifts (see e.g. Patel et al. 2013b, van der Wel et al. 2014, Fagioli et al. 2016), poses tight constraints on any formation model. From the observed age distribution of stars in normal massive early-type galaxies we know that the substantial observed evolution was not caused primarily by the addition of newly formed stars but rather the addition and rearrangement of old stars in these systems.
1.3.3. Evolution of spiral galaxies The high-redshift progenitors of Milky Way like disk systems are also smaller than local examples of similar systems and have formed half of their mass below z ∼ 1. Most of the mass is assembling at larger radii by in-situ star formation providing direct evidence for 'inside-out' growth accompanied by mass growth in the central regions which can be dominated by bars and bulges (Patel et al. 2013a). The central mass growth might originate from secular instabilities or merger events, but most stars currently in spiral systems were made from gas added to them rather than from accreted stars or stellar systems. In general the size evolution of spiral systems is, however, significantly less rapid than for early-type galaxies (van der Wel et al. 2014).
1.3.4. Evolution of star formation rates and gas fractions A significant fraction (if not most) of stars in the Universe are formed in galaxies with star formation rates that are almost linearly related to their stellar mass (the star formation main sequence) since z ∼ 2.5 (see e.g. Noeske et al. 2007, Daddi et al. 2007, Whitaker et al. 2012, Renzini & Peng 2015). The tightness of the overall relation and the mostly disk-like morphology (Genzel et al. 2006, Förster Schreiber et al. 2009) of the highly star forming systems indicates that major merger driven starbursts are of minor importance for the universal star formation budget. The increase in star formation rate (the normalization of the main-sequence) towards high redshift is accompanied by increasing gas fractions reaching up to ∼ 50% at redshift z ∼ 2 (e.g. Tacconi et al. 2010, Daddi et al. 2010, Tacconi et al. 2013). This buttresses the simple picture that most star-formation comes from the gradual transformation of accumulated gas into stars.
Let us return now to the physics problem to be solved given this observational background. First we look at what we have described as part (A) the evolution of radiation fields, dark matter and gas in the standard cosmological paradigm. This has been well summarized in several recent textbooks (e.g. Mo, van den Bosch & White 2010), so only some of the highlights need to be mentioned. A spectrum of adiabatic perturbations is imprinted onto the three components at high redshift producing cosmic microwave background radiation (CBR) fluctuations emitted at roughly redshift 1000, the analysis of which (cf. WMAP, Planck) uniquely specifies the cosmological model (Spergel et al. 2007, Planck Collaboration et al. 2014). If we take that to be the simplest one compatible with the data (the ΛCDM cosmologically flat model), the model can be defined by five to six independent parameters that are typically known now (primarily, but not entirely from analysis of the CBR) to high accuracy. The composition of the dark matter remains unknown but the standard 'cold dark matter' model has been so successful that the principle remaining alternatives, Warm Dark Matter or Fuzzy Dark Matter behave essentially like ΛCDM on all large scales with (interesting) deviations becoming apparent below ∼ 1 kpc.
1.4.1. Direct simulations of dark matter Accepting this model we can specify in a cosmologically representative volume the statistical distribution of gas, dark matter and radiation in a fashion sufficiently detailed to provide initial conditions for computation of the evolution of the various components. In the simplest treatments of this evolution, where dark matter is followed via Newton's laws and the transformation of gas into stars and black holes is ignored. Many different groups have worked on the problem producing extraordinarily successful (and convergent) results (see Frenk & White 2012). The Millennium simulation (Springel et al. 2005) was perhaps the most publicly successful such dark matter calculation, but other simulations (Klypin, Trujillo-Gomez & Primack 2011) also of larger volumes (Angulo et al. 2012) or constrained to a certain halo mass scale (Diemand, Kuhlen & Madau 2007, Springel et al. 2008, Stadel et al. 2009, Gao et al. 2012) have made very important contributions. This is problem (A) and it is essentially a solved problem. But it leaves us a long way from understanding the evolution of real galaxies composed primarily of stars.
1.4.2. Semi-analytical models for baryons There exist different approaches to the more difficult part (B), the allowance for star and black hole formation and the input from these sources of mass, energy, momentum and processed matter back into the gaseous component. The first approach to this hard problem was to set up comprehensible 'model problems' the solutions of which would be illuminating. One large class of such efforts has been broadly labeled the 'semi-analytic' method, where one takes the dark matter simulations as a given, and then tries, by one means or another, to estimate how the other components will react. Examples of progress made in the late 90's via the setting and solving of very informative 'model problems' consider the formation of disks from gas accumulating within dark matter halos (Dalcanton, Spergel & Summers 1997, Mo, Mao & White 1998). Modern attempts to input what are thought to be the most important physical processes in a simple fashion (e.g. Kauffmann, White & Guiderdoni 1993, Somerville & Primack 1999, Croton et al. 2006, Bower et al. 2006, Guo et al. 2011, Henriques et al. 2015) aim at finding that set which best produces realistic mock observations (see review by Somerville & Davé 2015). Another class of more analytical models makes the simplifying assumption that star forming galaxies evolve in a quasi-equilibrium fashion regulated by gas inflow and outflow, star formation and the change of mass in the galactic gas reservoir. The above approaches are extensively reviewed in Somerville & Davé (2015).
1.4.3. Direct simulations including baryons While these methods have been most helpful in furthering our understanding, the technical and algorithmic progress has enabled the direct and ambitious effort to include as much of the detailed physics as possible and simply compute forwards from the well established initial conditions to the current time using gravity, hydrodynamics, radiation transfer and all of the elaborate apparatus developed by physics to address continuum mechanics. The computational tools to follow the evolution of dark matter and stars (gravity) as well as gas (hydrodynamics) have been developed since the early 1980s.
The first three-dimensional coupled hydrodynamical simulations including self-gravity used the smoothed particle hydrodynamics (SPH) technique (Efstathiou & Eastwood 1981, Evrard 1988, Hernquist & Katz 1989). The Lagrangian particle based SPH method (Gingold & Monaghan 1977, Lucy 1977, see also Springel 2010b and Somerville & Davé 2015 for recent reviews) is relatively simple to implement and due to its adaptive spatial resolution and good conservation properties has been very popular for galaxy formation simulations until today. However, the basic implementation has to be modified for typical astrophysical conditions including shocks, shear and large temperature gradients and it has become clear that some standard implementations have serious difficulties to properly model fluid mixing and sub-sonic turbulence (Agertz et al. 2007, Springel 2010b). Most of the recent SPH work on cosmological galaxy formation is based on derivatives of either the GASOLINE (Wadsley, Stadel & Quinn 2004) code or the GADGET (Springel 2005) code and include updated implementations to treat the mixing problem better (see e.g. Wadsley, Veeravalli & Couchman 2008, Read & Hayfield 2012, Hu et al. 2014, Hopkins et al. 2014, Schaye et al. 2015, Schaller et al. 2015) and references therein). As an alternative to the SPH method particle based meshless-finite-mass and meshless-finite-volume methods have been proposed (Gaburov & Nitadori 2011). The recent GIZMO implementation is based on the GADGET framework and shows some significant improvements on idealised test problems, in particular for low Mach number gas (Hopkins 2015).
Eulerian hydrodynamic codes have also been widely used for cosmological simulations, some with adaptive mesh refinement capabilities. These codes typically perform better than SPH in terms of mixing and shock problems but might suffer from artifacts due to grid structure and numerical diffusion, which, for some solvers, can become significant. The first rough Eulerian treatment was by Cen & Ostriker (1992a) and the recently most used, greatly improved, Eulerian adaptive mesh refinement codes are ENZO (Bryan et al. 2014), RAMSES (Teyssier 2002), and ART (Kravtsov, Klypin & Khokhlov 1997) and also FLASH (Fryxell et al. 2000) as well as ATHENA (Stone et al. 2008) for ISM simulations on smaller scales. The newly developed moving mesh code AREPO (Springel 2010a) similarly suffers from numerical diffusion but combines advantages of the Lagrangian and Eulerian approaches and performs much better than traditional SPH codes like GADGET on mixing problems with a high convergence rate (Springel 2010b, Sijacki et al. 2012).
There are ongoing efforts to better understand the strengths and weaknesses of different numerical schemes (e.g. Price & Federrath 2010, Heitsch, Naab & Walch 2011, Hubber, Falle & Goodwin 2013, Hayward et al. 2014, Kim et al. 2014) and to constantly improve on accuracy and performance of all major codes. It has been realized early on that different numerical schemes applied to cosmological simulations can result in systems with different physical properties (Frenk et al. 1999), even if only gravity and hydrodynamics are considered. In addition, there is a wealth of published sub-resolution models (see Section 2.2.1) which are used to model galaxy formation. These models are often designed for particular numerical schemes and introduce even stronger variations in physical properties for a given set of initial conditions (Scannapieco et al. 2012). One of the major challenges in computational galaxy formation is to further improve on the numerical schemes and reduce the contribution of sub-resolution modeling to numerically resolved physical scenarios.
These numerical methods, which we could label 'ab initio' computations aiming to solve part (B), will be discussed in the second part of this review. But first we will address two other extremely useful idealized and empirical approaches which preceded and accompanied them.
1.5. Disks, Ellipticals and Mergers - a very useful set of idealized simulations
In the early 70s a definite cosmological model had not emerged and the computational resources as well as the numerical algorithms were still limited. This was the start of idealized merger simulations as it had been realized that galaxies actually interact and merge for bridges, tidal tails and other merger phenomena are observed (Toomre & Toomre 1972, Joseph & Wright 1985, Sanders et al. 1988). Early self-consistent N-body simulations (e.g. White 1978) were limited to the stellar component of galaxies with a few hundred gravitating particles (stars), a situation that has significantly improved until now when millions of star particles, dark matter particles and complicated gas dynamical processes can be studied (e.g. Hopkins et al. 2013). With methods for creating equilibrium models for multi-component galaxies (i.e. Hernquist 1993a) it became possible to simulate the evolution of the stellar and gaseous components of disk galaxies in more detail. For more than 20 years such setups are playing a major role for developing star formation and feedback models in direct comparison with observations of star forming spiral galaxies (e.g. Mihos & Hernquist 1994b, Springel & Hernquist 2003, Li, Mac Low & Klessen 2005, Dalla Vecchia & Schaye 2008, Hopkins, Quataert & Murray 2011, Agertz et al. 2013). In most cases it is tested under which conditions a given model reproduces the observed relation between gas surface density and star formation rate surface density (Kennicutt 1998). Only successful models are then considered for more complex simulations of galaxy mergers or the cosmological formation of galaxies.
A number of important physical processes have been investigated with merger simulations and the insight into galaxy formation physics has been significant. We know that equal-mass mergers are rare and relatively unimportant for the cosmic star formation budget (see Sec. 1.3.4 and Man et al. 2012, Bluck et al. 2009, Williams, Quadri & Franx 2011). For intermediate mass galaxies (e.g. Milky Way) and low mass systems stars are primarily formed from streams of gas that accumulate centrally or in disks (e.g. Rodriguez-Gomez et al. 2016, Qu et al. 2017). For high mass systems (i.e. massive early-type galaxies) mergers become important. Stars added in major and minor mergers can make up as much as 50% of the largely outer envelopes (in case of minor mergers) of these systems (Naab, Johansson & Ostriker 2009, Rodriguez-Gomez et al. 2016, Qu et al. 2017). But the initial proposal that normal ellipticals are made by morphological transformations of disk galaxies in binary major mergers of spirals, though not generally applicable (Ostriker 1980), is influential and instructive. In particular, it was shown that observed nearby disk galaxy mergers most likely evolve into systems with structural similarities to young early-type galaxies (e.g. Rothberg & Joseph 2004).
1.5.1. Collisionless mergers Merger simulations might be separated into two groups. Collisionless simulations of stars and dark matter mutually interacting by gravity alone were evolved by the collsionless Boltzmann equation (see e.g. Binney & Tremaine 2008). Such idealized systems can be considered energy conserving (no radiative losses). In reality almost no galactic system meets these conditions. Even massive galaxies have some amount of hot and cold gas (e.g. Sun et al. 2009, Young et al. 2011, Serra et al. 2012). But if the gas components can be considered dynamically unimportant it is justified to consider a system collisionless (the term 'dry' has been used in the literature). When spheroidal one-component systems merge, their structural evolution can -to good accuracy - be estimated using the virial theorem with only a few assumptions (Cole et al. 2000, Naab, Johansson & Ostriker 2009, Bezanson et al. 2009). Following Naab, Johansson & Ostriker (2009) one can assume that a compact initial stellar system has formed (e.g. involving gas dissipation) with a total energy Ei, a mass Mi, a gravitational radius rg,i, and the mean square speed of the stars is ⟨ vi2⟩. According to the virial theorem (Binney & Tremaine 2008) the total energy of the system is
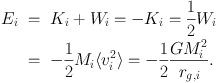 |
(1) |
This system then merges (on zero energy orbits) with other systems of a total energy Ea, total mass Ma, gravitational radii ra and mean square speeds averaging ⟨ va2⟩. The fractional mass increase from all the merged galaxies is η = Ma / Mi and the total kinetic energy of the material is Ka = (1/2) Ma ⟨ va2⟩, further defining є = ⟨ va2 ⟩ / ⟨ vi2⟩ . Here є = 1 represents an equal mass merger and є ∼ 0 for very minor mergers. Under the assumption of energy conservation (e.g. Khochfar & Burkert 2006 indicate that most dark matter halos merge on parabolic orbits) the ratio of initial to final mean square speeds, gravitational radii and densities can be expressed as
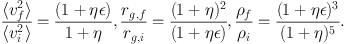 |
For binary mergers of identical systems, η = 1, the mean square speed remains unchanged, the size increases by a factor of two and the densities decrease by a factor of four. In the limit that the mass is accreted in the form of a weakly bound stellar systems with ⟨ va2⟩ << ⟨ vi2⟩ or є << 1, the mean square speed is reduced by a factor two, the size increases by a factor four and the density drops by a factor of 32. These estimates are, however, idealized assuming one-component systems, no violent relaxation and zero-energy orbits with fixed angular momentum. In the presence of a dark matter halo the structural changes become more complicated and e.g. the fraction of dark matter at the center (inside the half-mass radius of the stars) may increase due to violent relaxation (Boylan-Kolchin, Ma & Quataert 2005, Hilz et al. 2012). In general a fraction of the orbital angular momentum of the galaxies will be transferred to rotation in the central galaxy, so that the merger remnants in most cases rotate significantly (White 1979a, Naab, Khochfar & Burkert 2006, Di Matteo et al. 2009a, Bois et al. 2010, Bois 2011). Major mergers of spheroidal galaxies are also expected to flatten existing abundance gradients (White 1979b, Di Matteo et al. 2009b).
If a spheroidal system experiences collisionless minor mergers (with satellite galaxies of much lower mass than the central) violent relaxation effects in the central galaxy are negligible and the satellite stars are stripped at larger radii (Villumsen 1983), a mechanism that offers a plausible explanation for the observed structural evolution of massive galaxies (Nipoti, Londrillo & Ciotti 2003, Hilz et al. 2012) and the formation of extended stellar envelopes in early-type galaxies leading to the very high observed Sersic indices and outer metallicity gradients (Villumsen 1983, Hilz, Naab & Ostriker 2013). Whether minor mergers alone can explain the observed strong size evolution of massive early-type galaxies will depend on the actual merger rates as well as the structure of the satellite galaxies (Nipoti et al. 2009, Cimatti, Nipoti & Cassata 2012, Newman et al. 2012a, Oogi & Habe 2013, Bédorf & Portegies Zwart 2013). Per added unit of stellar mass this process can also increase the fraction of dark matter within a half-mass radius more efficiently than major mergers (Boylan-Kolchin, Ma & Quataert 2005, Hilz, Naab & Ostriker 2013).
Another important process investigated is the morphological transformation of kinematically cold disk galaxies to kinematically hot spheroidal galaxies (Farouki & Shapiro 1982, Negroponte & White 1983, Barnes & Hernquist 1992, Barnes 1992, Hernquist 1992). Violent relaxation heats the disk stars and some fraction of the orbital angular momentum and of the spin of the initial disk systems can be absorbed by the dark matter halos (Barnes 1988). This results in stellar remnants that can have early-type galaxy morphology and kinematics if the progenitor galaxies had a bulge component of sufficiently high phase space density (Hernquist 1993b). Therefore merging is important for the formatin of hot stellar systems. Depending on the mass-ratio of the merging disks - and the amount of 'damage' that is done to the primary disk, the remnants rotate fast or slow, have disky, round or boxy isophotal shapes and are more or less flattened (Barnes 1998, Bekki 1998, Heyl, Hernquist & Spergel 1994, Naab, Burkert & Hernquist 1999, Bendo & Barnes 2000, Cretton et al. 2001, Naab & Burkert 2003, Bournaud, Combes & Jog 2004, Bournaud, Jog & Combes 2005, González-García & Balcells 2005, Jesseit et al. 2009). For very low mass infalling systems the disk might be only moderately heated and retains its flat and rotationally supported morphology for single events (Quinn, Hernquist & Fullagar 1993, Velazquez & White 1999). Repeated minor mergers will make the initial disk system more spherical and reduce its spin (Bournaud, Jog & Combes 2007, Qu et al. 2010).
1.5.2. Mergers with gas A major step in understanding galaxy mergers was established once the simulations included a dissipative gas component. The gravitational torques exerted on the gas during the merger were able to drive the gas from large radii to the nuclear regions of the merger remnant once it lost its rotational support in tidally induced shocks (Barnes & Hernquist 1996). This has important implications for galaxy formation. Using sub-resolution models for the conversion of gas into stars (see Section 2.1), it was shown by many studies that the gas inflow can trigger a nuclear starburst similar to what is observed in ultra-luminous infrared galaxies (ULIRGS) and explain observations of 'extra light' in the centers of low mass early-type galaxies (Mihos & Hernquist 1994a, c, 1996, Kormendy 1999, Springel 2000, Hopkins et al. 2009a, c, Kormendy et al. 2009, Teyssier, Chapon & Bournaud 2010, Hopkins et al. 2013, Hayward et al. 2014). Gas accumulating at the center of merger remnants also makes the potential more spherical, favoring the population of stars on tube orbits (Barnes & Hernquist 1996, Jesseit, Naab & Burkert 2007). As a result, rotating remnants of gas rich mergers can form disk-like subsystems (Bekki & Shioya 1997, Bendo & Barnes 2000, Barnes 2002, Jesseit, Naab & Burkert 2007, Jesseit et al. 2009) and show observed line-of-sight velocity distributions with steep leading wings, which is not the case if gas is neglected (Naab, Jesseit & Burkert 2006, Hoffman et al. 2009, 2010).
The effect of dissipation in binary galaxy mergers has also been used to explain the detailed shape of scaling relations and the fundamental plane and its potential evolution with redshift (Cox et al. 2006a, b, Dekel & Cox 2006, Robertson et al. 2006b, Hopkins et al. 2009b). One branch of binary merger simulations focused on the potential feeding of supermassive black holes, which are observed in most nearby early-type galaxies. Here the merger-triggered inflow provides the low angular momentum gas to be accreted onto the black hole (Hernquist 1989). The energy released from the accreting black hole, on the other hand, has been suggested to drive gas out of the merger remnant, significantly reducing its star formation rate (Springel, Di Matteo & Hernquist 2005a). The idea of 'black hole feedback' to 'quench massive galaxies' was born. Assuming a Bondi-like accretion and a relatively simple scaling for energy feedback in a sub-resolution model , it was also possible to provide an explanation for the observed stellar mass black hole mass relation (Di Matteo, Springel & Hernquist 2005). This finding has led to a number of studies, based on idealized binary merger simulations investigating the evolution of the Mbulge − MBH and σbulge − MBH relation (e.g. Robertson et al. 2006c, Johansson, Naab & Burkert 2009, Debuhr et al. 2010, Debuhr, Quataert & Ma 2011, Choi et al. 2014, Barai et al. 2014) and the evolution of the quasar luminosity function based on the assumption that most of the AGN activity is driven by galaxy mergers (e.g. Hopkins et al. 2005, 2006).
Despite the explanatory successes of these studies, the drawback of idealized sub-resolution models used is that the actual physical processes (e.g. the feedback from central super-massive black holes) cannot be resolved and the cosmological context is omitted. This is true for most merger simulations even though the typical spatial and mass resolution is much higher than in larger scale cosmological simulations (Section 2). The assumptions are mostly simple and physical effects are condensed or hidden in parameters or scale factors, which are often scaled to a specific set of observations (see Section 1.1). Therefore the validity of the astrophysical implications always remains somewhat uncertain. For example many models adopted in binary merger simulations use a simple accretion scheme to determine the mass flow rates onto the black holes. The accretion rate depends on the sound-speed of the surrounding medium, which can vary significantly depending on the assumed star formation and feedback model (see Section 2.3). Alternative models link the accretion rates to gravitational instabilities and torques (Hopkins & Quataert 2011, Hopkins et al. 2012). Some models used for binary merger simulations assume feedback in the form of thermal energy to the gas surrounding the black hole (Springel, Di Matteo & Hernquist 2005a), others take into account the observed momentum output which significantly reduces the amount of hot coronal gas and the observable X-ray luminosities (Debuhr, Quataert & Ma 2011, Choi et al. 2014). Binary merger experiments have been used as test beds for sub-resolution models used in larger scale cosmological simulations.
1.5.3. Caveats of the merger hypothesis The importance of major mergers for the formation and evolution of massive galaxies is still under debate. Idealized merger simulations ignore the cosmological context where gas accretion, repeated minor mergers as well as environmental effects are important. As the expected major merger rates are low some massive galaxies might experience no major merger at all (see Fig. 1). It is clear that galaxy mergers, in particular of equal mass, can have a significant impact on galaxy kinematics and mass growth if they happen at late times. The importance of stars formed in merger-triggered starbursts may have been overestimated as well, in particular due to the fact that most merger simulations ignored halo gas accretion. If halo accretion is included the disks have more realistic constant star formation rates and the contribution from merger triggered star formation is significantly lower and sometimes negligible (Moster et al. 2011). This is supported by observations indicating that most star formation in the Universe happens in relatively normal morphologically settled disk-like galaxies (e.g. Daddi et al. 2007). Merging systems with enhanced star formation rates seem to be of minor importance but might help in the transition to quenched early-type galaxies (Wuyts et al. 2011). Observations at low and high redshift also provide evidence that significant black hole accretion is not solely connected to merging but also gas rich disk like galaxies can host AGN of significant luminosity (Georgakakis et al. 2009, Cisternas et al. 2011, Schawinski et al. 2011, Kocevski et al. 2012). Also, cooling flow instabilities within the hot gas of elliptical galaxies lead to a secular branch of AGN fueling. Apparently major mergers can host luminous AGN but by no means are all AGN induced by mergers. Also it seems unlikely that the population of present day early type galaxies can have directly formed via mergers among the population of present day disk galaxies and their progenitors, as the early-type population is too old, too massive and too metal rich (Naab & Ostriker 2009). At earlier times the discrepancy in mass and size between observed Milky Way progenitors and massive early-type galaxies is even more pronounced (Patel et al. 2013a).
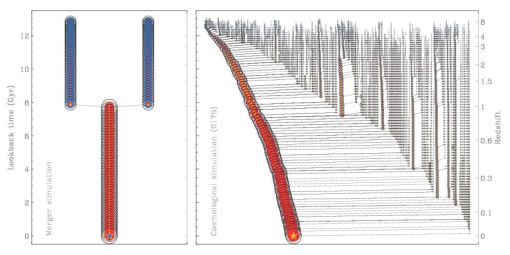 |
Figure 1. Binary disk merger simulations are useful in understanding merging disk galaxies observed in the sky. In general, they lack the realism and complexity of the cosmological assembly of old massive early-type galaxies. In the left panel we show a schematic and very simplified binary disk 'merger-tree'. Two gas-rich (blue) stellar (yellow) disks with little hot gas (red) merge at z ≈ 1 and form an elliptical galaxy. In a cosmological zoom simulation (right panel) of the formation of a dark matter halo (black circles) and its massive galaxy (cold gas: blue) is significantly more complex. It is evident that continuous infall of matter in small and large units is an important characteristic of the assembly of massive galaxies. The galaxy shown (0175 from Oser et al. 2010) is another extreme case as it has no major merger since z ≈ 3. Others galaxies of similar mass can have up to three major mergers. Major mergers definitely happen and they have a strong impact on galaxy evolution. Cosmological assembly and mass growth, however, is always accompanied by numerous minor mergers and gas accretion (figure from Naab et al. 2014). |
A fundamental question in galaxy formation, embedded in the modern hierarchical cold dark matter framework, is how much of the available baryonic matter is converted into stars in the central galaxies in dark matter halos. This quantity might be termed galaxy formation efficiency or galaxy fraction fgal. There have been a number of attempts to estimate this number for the Milky Way. Whereas the stellar mass of the Milky Way is relatively well determined (Rix & Bovy 2013), the major uncertainty is in the mass of the Milky Way's dark matter halo. Typically mass estimates are in the range of 1 − 2 × 1012 M⊙ (Xue et al. 2008, Li & White 2008, Bovy et al. 2012, Watkins, Evans & An 2010, Bland-Hawthorn & Gerhard 2016). The masses result in galaxy fractions of fgal ∼ 20 − 40%. With much better observed stellar mass functions at low and high redshifts and converged dark matter simulations for a given cosmological model, it has become possible to estimate the galaxy formation efficiency (or the relation of galaxy mass to halo mass) for a large range of halo masses locally and at higher redshifts. The methods used include halo occupation distribution modeling (Berlind & Weinberg 2002, Bullock, Wechsler & Somerville 2002, Kravtsov et al. 2004), conditional luminosity function modeling (Yang, Mo & van den Bosch 2003) or a rank ordered matching of observed galaxy mass functions to simulated halo mass functions (Vale & Ostriker 2004, 2006, Shankar et al. 2006, Conroy, Wechsler & Kravtsov 2006, Behroozi, Conroy & Wechsler 2010, Moster et al. 2010, Moster, Naab & White 2013, Behroozi, Wechsler & Conroy 2013, Hearin & Watson 2013, Lu et al. 2015).
Most of these studies indicate that around 10 - 20% of the available baryons are converted into stars in dark matter halos of ∼ 1012 M⊙. This fraction is lower in dark matter halos of higher and lower mass with considerable uncertainties at both ends (see e.g. Gonzalez et al. 2013, Kravtsov, Vikhlinin & Meshscheryakov 2014, Guo & White 2014). The mismatch of most early cosmological simulations with these empirical estimates was highlighted in (Guo et al. 2010) and galaxy fractions became a standard test presented in almost every publication about cosmological simulations. Also at higher redshift the tension with simulations was formerly much more severe (see e.g. Moster, Naab & White 2013) due to the overly efficient early conversion of baryons into stars.
The matching models also provide an independent estimate of the amount of stars formed in the galaxies (in-situ star formation as measured by the star formation rates) and the amount of stars accreted in galaxy mergers. The general conclusion is that all galaxies are dominated by in-situ star formation at high redshift (z ≳ 1.5). A trend that continues to low redshift for moderate mass (Milky Way type) galaxies which are predicted to have accreted between 5% (Moster, Naab & White 2013) and 30% (Behroozi, Wechsler & Conroy 2013) of their stellar mass. High mass galaxies assemble more and more of their stellar mass by mergers towards lower redshifts. However, the estimated fractions of accreted stars by z = 0 of galaxies in massive halos (Mhalo ∼ 1013) vary significantly between 20% and 60% (Moster, Naab & White 2013, Behroozi, Wechsler & Conroy 2013, Yang et al. 2013). The general trend is similar to simulations (e.g. Oser et al. 2010, Lackner et al. 2012, Gabor & Davé 2012, Rodriguez-Gomez et al. 2016, Qu et al. 2017). It has also been highlighted that galaxies in massive halos (Mhalo ≳ 1013 M⊙) form their stars before the halo assembles. Low mass galaxies form their stellar components after their halos assemble (Conroy & Wechsler 2009).