


In rotating spiral galaxies, the circular velocity at radius r relates directly to enclosed mass via vcirc2 = GM(r) / r. Ordered rotation in dSphs is dynamically negligible (see next section); instead, dSphs receive support against gravity primarily from the random motions of their stars. Therefore the estimation of dSph masses is a fundamentally statistical enterprise. The simplest statistic that characterises dSph stellar dynamics is the dispersion of velocities along the line of sight, σ. For a relaxed system of characteristic size R, the virial theorem implies σ2 ∝ GM / R. In principle, measurements of a dSph's size and velocity dispersion provide a simple estimate of its mass (Section 4). In practice, one must be aware of effects that can inflate measured values of the velocity dispersion above equilibrium values.
In the simplest case, solid-body rotation about an axis misaligned with the line of sight will induce a gradient, dV / dR, in the line-of-sight velocity distribution. For example, Figure 14 plots mean velocity along the axes for which the observed velocity gradients are maximal in Carina, Fornax, Sculptor and Sextans. Even at the radii of the outermost observed stars, any ordered motion due to rotation is limited to Rmax dV / dR ≲ 3 km s−1, negligible compared with the observed velocity dispersions of σ ∼ 10 km s−1.
For Carina and Fornax the amplitude and orientation of the observed velocity gradients are consistent with a perspective effect induced not by rotation, but rather by these dSphs’ systemic orbital motions transverse to the line of sight (Kaplinghat & Strigari, 2008, Walker et al., 2008), as measured from HST astrometry (Piatek et al., 2002, 2003, 2007). The observed signal in Sculptor cannot be attributed to its measured proper motion (Schweitzer et al., 1995, Piatek et al., 2006), and thus Sculptor may have a residual rotational component (Battaglia et al., 2008), albeit one that contributes weakly (vrot / σ ≲ 0.5) to the measured velocity dispersion.
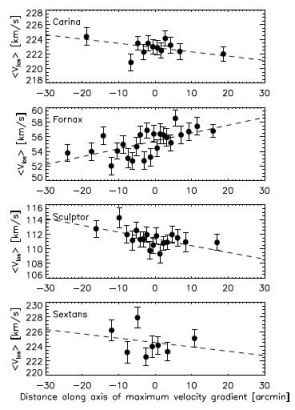 |
Figure 14. Line-of-sight velocity gradients in the Milky Way's ‘classical’ dSph satellites. Panels display mean velocity as a function of distance along the axis corresponding to the maximum velocity gradient, from the samples of Walker, Mateo & Olszewski (2009). The observed gradients give rise to maximum amplitudes Rmax dV / dR ≲ 3 km s−1, significantly less than the velocity dispersions (σ ∼ 10 km s−1). Using VLT spectra from the DART survey, Battaglia et al. (2008) report similar results for Sculptor, measuring a gradient of 7.6−2.2+3.0 km s−1 deg−1 along the morphological major axis. |
All dSphs considered here orbit within the gravitational potential of the Milky Way and are therefore susceptible to external influence from tidal forces. Tides can affect the structure and kinematics of a given satellite through a variety of mechanisms, including stripping, shocking, ‘stirring’ and various orbital resonances. Depending on the strengths of interactions and timescales of subsequent relaxation, tides might inflate observed velocity dispersions and mass estimates based thereupon.
In the most extreme scenarios, tides have been invoked to explain dSph velocity dispersions without dark matter (e.g., Kuhn & Miller, 1989, Kuhn, 1993, Kroupa, 1997, Fleck & Kuhn, 2003, Metz & Kroupa, 2007). Such explanations are most plausible for dSphs that are closest to the Milky Way and exhibit elongated stellar structures, e.g., Ursa Major II (Zucker et al., 2006a, Muñoz et al., 2010), Hercules (Belokurov et al., 2007, Coleman et al., 2007, Martin & Jin, 2010), and possibly Segue 1 (Niederste-Ostholt et al., 2009). However, generalisation of purely tidal mechanisms to explain the apparent dark matter content of the entire dSph population does not account without contrivance for the wide distribution of dSph distances (∼ 30 ≲ D / kpc ≲ 250) or for a monotonic metallicity-luminosity relation (Mateo, 1998, Kirby et al., 2008, 2011).
While tidal stripping involves the transfer of mass from the satellite to the parent outside a particular boundary 6, tidal ‘shocking’ involves impulsive injection of energy into the satellite as it plunges through the disk and/or near the center of the parent system (e.g., Gnedin et al., 1999). While the former process removes mass preferentially from the satellite's outer regions, the latter process tends to decrease its central density (Read et al., 2006a). Early numerical simulations by Piatek & Pryor (1995) and Oh, Lin & Aarseth (1995) suggest that even strong tidal interactions do not significantly inflate a satellite's central velocity dispersion, which therefore can remain a reliable indicator of dynamical mass.
Many recent N-body simulations examine specific phenomenology associated with tidal interactions. For example, Read et al. (2006a) use simulations to demonstrate that the projection of tidal streaming motions along most viewing angles tends to cause velocity dispersion profiles to increase at large radius, and then argue that the lack of such upturns in the classical dSphs (with the possible exception of Draco — see Figure 12) limits the severity of current disruption events. Peñarrubia et al. (2008) use simulations to show that repeated tidal encounters cause monotonic declines in equilibrium values (as evaluated at apocenter) of the satellite's central surface brightness, velocity dispersion and scale radius. Further simulations by Peñarrubia et al. (2009) indicate that when a dark matter halo is present, tides do not generate a clear truncation in the surface brightness profile of the bound remnant, as otherwise is prescribed by the self-consistent dynamical model of King (1966). Rather, as the bound remnant relaxes after a pericentric encounter, tidal debris generates an ‘excess’ of stars at radii where the local crossing time (Rc / σ ∼ 10 Myr at the core radius of a typical dSph) exceeds the time elapsed since the encounter.
Such simulations provide a context for evaluating the tidal origin of breaks and bumps in observed surface brightness profiles of individual dSphs (Section 2.2.3 and Figure 2), and for gauging the severity with which tides influence the observed kinematics. In general, one can expect tides to have stronger and more enduring influence on the outer regions of dSphs, and for the degree of influence on any particular satellite to scale with orbital parameters. A typical dSph with Rc ∼ 100 pc and σ ∼ 10 km s−1 requires ∼ 20 core crossing times to travel a distance of ∼ 100 kpc (a typical Galactocentric distance) at speed ∼ 250 km s−1; the assumption of dynamic equilibrium should therefore hold reasonably well out to several core radii for the majority of dSphs. In practice one must use all available information about a satellite's orbit and outer structure to evaluate the likely contribution of tides on a case-by-case basis.
Unresolved binary orbital motions might contribute significantly to the observed velocity dispersions of the least massive galaxies. Olszewski et al. (1995) use 112 independent velocity measurements for 42 stars in Draco and Ursa Minor to identify seven stars that exhibit velocity variability. Elimination of these stars from their samples has negligible impact on the measured velocity dispersions of Draco and Ursa Minor. Using the larger KPNO/HYDRA sample of (Armandroff et al., 1995) (373 independent velocity measurements for 185 stars), Olszewski et al. (1996) perform Monte Carlo simulations to estimate that the binary frequency for Draco and Ursa Minor stars with periods of ∼ 1 year is ∼ 0.2−0.3 per decade of period. Even though this fraction is larger than the one found in the solar neighborhood (e.g., Duquennoy & Mayor, 1991), further simulations by Olszewski et al. (1996) and Hargreaves et al. (1996a) demonstrate that the scatter introduced by binaries is small compared to the measured dispersions of σ∼ 10 km s−1, and thus that binaries do not significantly inflate dynamical masses of the ‘classical’ dSphs.
More recently, measurements of velocity dispersions as small as σ ∼ 3 km s−1 for several ultrafaint satellites (Simon & Geha, 2007, Martin et al., 2007, Walker et al., 2009a, Adén et al., 2009, Koposov et al., 2011b) have renewed concerns over the possible contribution of binary motions. While simulations by Minor et al. (2010) find that binaries have little effect on dispersions measured for systems with intrinsic velocity dispersions σ ≳ 4 km s−1, complementary simulations by McConnachie & Côté (2010) demonstrate that for systems with intrinsic dispersions near zero (as would be expected for many of the ultrafaints if they contain no dark matter), binaries can inflate measured dispersions to values as high as σ ∼ 4 km s−1.
It is therefore necessary to verify the extreme mass-to-light ratios of the faintest (and coldest) dSphs with repeat spectroscopic measurements that constrain the velocity variability of individual stars. Simon et al. (2011) present second-epoch Keck/DEIMOS velocity measurements for several of the Segue 1 stars first measured by Geha et al. (2009). They find that one of Segue 1's six red giants shows significant velocity variability, as do two fainter stars. Including parametric binary orbital distribution functions in a Bayesian analysis of Segue 1's velocity dispersion, Simon et al. (2011, see also Martinez et al. 2011) estimate a velocity dispersion of 3.7−1.1+1.4 km s−1, implying a dynamical mass-to-light ratio of M / LV ∼ 3400 [M / LV]⊙ and reinforcing their previous conclusion that Segue 1 is the ‘darkest’ galaxy known.
In a separate study, Koposov et al. (2011b) use ∼ 15 VLT/FLAMES observations obtained over one month in order to resolve binary motions directly among members of Boötes I. Figure 15 displays independent velocity measurements for two stars as a function of time. While velocities for the star in the left-hand panel are consistent with a constant velocity, velocities for the star in the right-hand panel change systematically by ∼ 10 km s−1. After discarding probable binaries, Koposov et al. (2011b) find that most members of Boötes I belong to a cold population with dispersion σ = 2.4−0.5+0.9 km s−1 (Figure 16), significantly smaller than previous single-epoch estimates of σ ∼ 6.5 km s−1 (Muñoz et al., 2006, Martin et al., 2007). At present the contribution of binaries to the velocity dispersions measured for the coldest dSphs is poorly understood, and more multi-epoch studies are required.
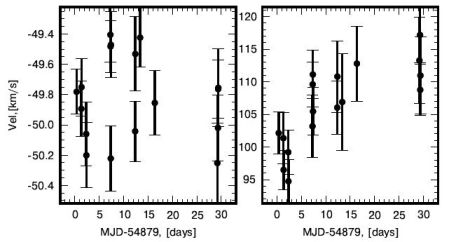 |
Figure 15. Direct detection of binary stars from individual velocity measurements in Boötes I (Koposov et al., 2011b, reproduced by permission of the American Astronomical Society). Left: foreground star with velocities consistent with a constant value. Right: member star (⟨ v⟩Boo ∼ 105 km s−1) exhibiting a velocity increase of ∼ 10 km s−1 over one month. See Section 3.3 for a discussion of the effects of binary orbital motions on measurements of dSph velocity dispersions. |
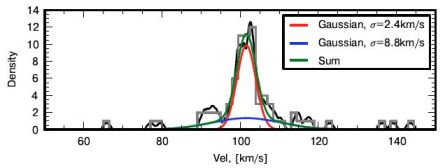 |
Figure 16. Velocity distribution of the Boötes I dSph, from the VLT/FLAMES data of Koposov et al. (2011b, reproduced by permission of the American Astronomical Society), not including 11 stars observed to have significant velocity variability. In the best-fitting two-Gaussian model, 70% of the stars belong to a ‘cold’ component with σ ∼ 2 km s−1 and the rest belong to a hotter component with σ ∼ 9 km s−1. |
6 Equation 4 gives the tidal radius for the idealised case of point-mass potentials. Calculations and simulations by Read et al. (2006b) demonstrate that stars are actually lost from various depths depending on the internal mass distributions of satellite and parent, as well as on the properties of the stellar orbits themselves (e.g., prograde versus retrograde with respect to the orbit of the dSph about the Galaxy). Back.