Copyright © 2011 by Annual Reviews. All rights reserved
| Annu. Rev. Astron. Astrophys. 2011. 49:409-470
Copyright © 2011 by Annual Reviews. All rights reserved |
The ΛCDM paradigm, while providing an excellent model for the large scale structure of the Universe, incorporates little information on the physical nature of dark matter. It assumes only that dark matter is non-baryonic; that it interacts weakly with baryonic matter and itself; that it emits and absorbs no detectable electromagnetic radiation; and that the dark matter particles move at sub-relativistic speeds.
As clusters merge under the pull of gravity, their dark matter halos and X-ray emitting gas can become separated temporarily, as the gas experiences ram pressure and is slowed. The observed offsets between the dark matter and X-ray peaks in the Bullet Cluster (1E 0657-558; Bradac et al. 2006; Clowe et al. 2006) and MACS J0025.4-1222 (Bradac et al. 2008a; Figure 17), both massive merging systems with relatively simple geometries, require conservatively that the scattering depth for the merging dark matter cannot be greater than one. Using gravitational lensing data to estimate the dark matter column densities through these clusters, Markevitch et al. (2004) and Bradac et al. (2008a) use the observed dark matter and X-ray peak separations to derive limits on the velocity-independent dark matter self-interaction cross-section per unit mass of σ/m < 5 cm2 g−1 and σ / m < 4 cm2 g−1 for 1E 0657-558 and MACS J0025.4-1222, respectively. Randall et al. (2008) additionally use the non-detection of an offset between the lensing peaks and the galaxy centroids for the Bullet Cluster to refine this constraint to σ/m < 1.5 cm2 g−1. Upcoming surveys (Section 6.1), should provide hundreds of similar examples, removing the current systematic limitations set by small number statistics. In combination with multiwavelength follow-up observations and improved numerical simulations (e.g., Forero-Romero, Gottlöber & Yepes 2010), this should allow the properties of dark matter in merging clusters to be studied in a robust, statistical manner.
 |
Figure 17. Hubble Space Telescope optical images of the massive, merging clusters 1E 0657-558 (z = 0.30) and MACS J0025.4-1222 (z = 0.54), with the X-ray emission measured with Chandra overlaid in pink and total mass reconstructions from gravitational lensing data in blue. The separations of the X-ray and lensing peaks, and the coincidence of the lensing and optical centroids, imply that the dark matter has a small self-interaction cross-section. Figure credits: Left: X-ray: NASA/CXC/CfA/M.Markevitch et al.; Optical: NASA/STScI; Magellan/U.Arizona/D.Clowe et al.; Lensing Map: NASA/STScI; ESO WFI; Magellan/U.Arizona/D.Clowe et al.; Right: X-ray: NASA/CXC/Stanford/S.Allen; Optical/Lensing: NASA/STScI/UC Santa Barbara/M.Bradač. |
One of the most remarkable predictions of the CDM model is that the density profiles of relaxed dark matter halos, on all resolvable mass scales, can be approximated by a simple, universal profile (Equation 15) with an inner, density slope ρDM ∝∼ r−1. In contrast, for dark matter models with significant self-interaction cross sections, halos are expected to exhibit flattened, quasi-isothermal cores (Spergel & Steinhardt 2000; Yoshida et al. 2000). In the absence of significant rotational support, these cores are also expected to be approximately spherical.
Using Chandra X-ray data for a sample of massive, dynamically relaxed galaxy clusters, (Schmidt & Allen 2007) measure a mean central density slope of −0.88 ± 0.29 (95 per cent confidence limits), in good agreement with ΛCDM. Detailed strong-plus-weak lensing analyses for a subset of these systems yields consistent constraints (Bradac et al. 2008b; Newman et al. 2009; 2011). On smaller scales, using stellar velocity dispersion profiles for the dominant cluster galaxies, Sand et al. (2008) (see also Newman et al. 2011) infer a possible flattening of the central dark matter halos in Abell 383 and MS 2137.3-2353. However, on these small scales, the impact of baryonic physics becomes important.
Arabadjis, Bautz & Garmire (2002) use the lack of a dark matter core in X-ray and lensing data for the relaxed cluster MS 1358+6245, to place a limit on the velocity independent dark matter particle-scattering cross section σ / m < 0.1 cm2 g−1. Miralda-Escudé (2002) use constraints on the ellipticity in the central regions of MS 2137.3-2353 to infer σ / m < 0.02 cm2 g−1. To improve these constraints, combined multiwavelength observations for large samples of relaxed clusters, coupled with improved simulations modeling fully the interactions between dark matter and baryons, are required.
Certain dark matter candidates, including sterile neutrinos, possess a two-body radiative decay channel that produces a photon with energy Eγ = MDM/2, where MDM is the dark matter particle mass (e.g. Feng 2010). Galaxy clusters have been the targets of searches for emission lines associated with such decays. The soft X-ray (keV) regime is particularly interesting, marking the lower limit of masses consistent with constraints from large scale structure formation. To date, all searches for monochromatic X-ray emission lines associated with non-baryonic matter in clusters (as well as other dark matter rich objects) have proved negative (e.g., Boyarsky et al. 2006; Riemer-Sorensen et al. 2007; Boyarsky, Ruchayskiy & Markevitch, 2008). Gamma-ray observations of clusters with the Fermi Gamma-ray Space Telescope have been used to place interesting upper limits on dark matter annihilation, and the lifetimes of particles for a range of masses and decay final states (Ackermann et al. 2010; Dugger, Jeltema & Profumo 2010).
Dark energy, though a key component of the standard cosmological model, provides by no means the only possible explanation for cosmic acceleration. Various non-standard gravity models can also produce acceleration on cosmological scales (for reviews, see Copeland, Sami & Tsujikawa 2006; Frieman, Turner & Huterer 2008). These include frameworks that consistently parametrize departures from General Relativity (GR; Hu & Sawicki 2007; Amin, Wagoner & Blandford 2008; Daniel et al. 2010); full, alternative theories such as the Dvali-Gabadadze-Porrati (DGP) braneworld gravity (Dvali, Gabadadze & Porrati 2000); f(R) modifications of the Einstein-Hilbert action (Carroll et al. 2004); and modifications of gravity based on the mechanism of ghost condensation (Hamed et al. 2004). A critical requirement for any modified gravity model is that it should mimic GR in the relatively small scale, high density regime where GR has been tested precisely. Thus, in addition to investigating whether dark energy is well described by a cosmological constant, we are simultaneously interested in asking whether GR provides the correct description of gravity, and indeed whether dark energy is needed at all.
To discriminate among these possibilities, and between particular dark energy and modified gravity models, it is important to combine expansion history data with measurements of the growth and scale-dependence of cosmic structure. Galaxy clusters provide some of our strongest constraints on structure growth. To utilize these constraints robustly, however, accurate predictions for the halo mass function are required. Recently, a few mass functions for specific modified gravity models have been constructed and calibrated using N-body simulations. These include the self-accelerated branch (Chan & Scoccimarro 2009; Schmidt 2009b) and normal branch (Schmidt 2009a) of DGP gravity, and an f(R) model (Schmidt et al. 2009). Constraints on the latter model using the observed local cluster abundance and other data are presented by Schmidt, Vikhlinin & Hu (2009).
An alternative to evaluating specific gravity theories is to adopt a convenient, parameterized description for the growth of structure. This can then be used to constrain departures from the predictions of ΛCDM+GR (Nesseris & Perivolaropoulos 2008). At late-times, the linear growth rate can be simply parametrized as (e.g. Linder 2005)
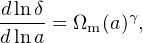 |
(26) |
where δ is the density contrast and γ the growth index. Conveniently, GR predicts a nearly constant and scale-independent value of γ ≈ 0.55 for models consistent with current expansion data. As in the case of w for dark energy models, constraining γ constitutes a phenomenological approach to studying gravity. Rapetti et al. (2009; 2010) report constraints on departures from GR on cosmic scales using this parameterization with cluster data. Their results are simultaneously consistent with GR (γ ∼ 0.55) and ΛCDM (w = −1) at the 68 per cent confidence level (left panel of Figure 18).
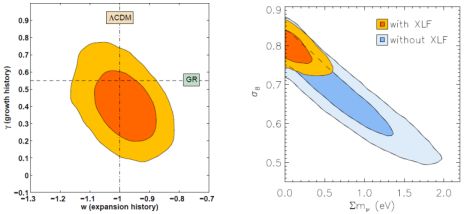 |
Figure 18. Left: Joint 68.3% and 95.4% confidence regions for departures from a General Relativistic growth history, parameterized by γ, and a ΛCDM expansion history, parameterized by w. The analysis uses a combination of cluster growth (XLF; Mantz et al. 2010b), fgas (Allen et al. 2008), WMAP (Dunkley et al. 2009), SNIa (Kowalski et al. 2008) and BAO (Percival et al. 2007) data. From Rapetti et al. 2010. Right: Constraints on neutrino mass and the amplitude of density perturbations for ΛCDM models, including global curvature and marginalized over the amplitude and spectral index of primordial tensor perturbations. Gold contours correspond to the same combination of data as in the left panel; blue contours show the strong degeneracy between neutrino mass and σ8 that exists when cluster growth data are not included in the analysis. From Mantz, Allen & Rapetti (2010). |
The mass of neutrinos directly influences the growth of cosmic structure, since any particle with non-zero mass at some point cools from a relativistic state, in which it effectively suppresses structure formation, to a non-relativistic state, in which it actively participates in the growth of structure (details are reviewed in Lesgourgues & Pastor 2006). In the standard scenerio where the neutrino species have approximately degenerate mass, the species-summed mass, ∑mν, is sufficient to describe their cosmological effects.
Although current data lack the precision to directly detect the effect of neutrino mass on the time-dependent growth of clusters, cluster data do play a key role in cosmological constraints on neutrinos when combined with CMB observations. On its own, the CMB can place only a relatively weak upper bound on the mass, ∑mν < 1.3eV at 95% confidence for a ΛCDM model (e.g. Dunkley et al. 2009; works discussed here used 5 years of WMAP data, but their conclusions are not significantly changed by the 7-year update). Incorporating cosmic distance measurements improves this to ∑mν < 0.61 eV, with the results displaying a strong degeneracy between ∑mν and the value of σ8 predicted from the amplitude of the primordial power spectrum, due to the integrated effect of neutrinos on the growth of structure. Cluster data at low redshift provide a direct measurement of σ8, breaking this degeneracy (right panel of Figure 18), improving the upper limit by a further factor of two, to ∑mν < 0.33 eV (Vikhlinin et al. 2009b; Mantz, Allen & Rapetti 2010; Reid et al. 2010). The degeneracy-breaking power of cluster observations also significantly improves the robustness of neutrino mass limits to the assumed cosmological model (e.g. marginalizing over global curvature; Mantz, Allen & Rapetti, 2010; Reid et al. 2010). In combination with Planck data, expected near-term improvements in cluster mass measurements from high-quality lensing data could reduce the limit on ∑mν to the point of distinguishing between the normal and inverted neutrino mass hierarchies.