


3. Transforming coordinates
Now that computerized data reductions of digital images (e.g., CCD frames) are commonplace, it is frequently necessary to transform positions of stars from one cartesian coordinate system to another. For most practical purposes we need only consider that the coordinate systems of two CCD frames (possibly from different telescopes) are related by a translation of the origin, a rotation, a scale change, and possibly a flip (for instance, if one frame is from a prime focus and the other is from a cassegrain focus), since the effects of higher-order distortions are usually negligible in a typical five-arcminute field of view. Therefore, our transformation equations can be written in the form
So, if we have n stars, we have 2n equations in four
unknowns: A, B,
and then to fool around with
First, let's rewrite our original equations a bit:
letting C =
(forgetting for the moment the possibility of a flip - I presume
you'll know ahead of time when you've got one). These can be rewritten
again,
and yet again,
where
Remember: I told you the tj, i can be anything you
can assign a
numerical value to. Now we can use vanilla least squares to get the
answers we want:
If you really want to know them, you can now compute
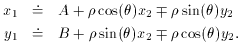
 , and
, and
 . The chintzy way out is to
solve the x and y equations
separately:
. The chintzy way out is to
solve the x and y equations
separately:
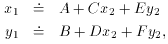
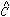 ,
,
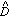 ,
,
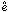 , and
, and
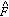 to get some compromise
average values for
to get some compromise
average values for  and
and  . There's a more elegant
way to do it,
however.
. There's a more elegant
way to do it,
however.
 cos(
cos( ) and D =
) and D =
 sin(
sin( ), we get
), we get
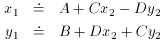
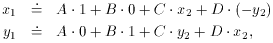
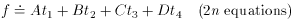
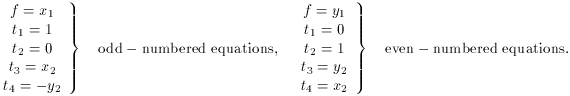
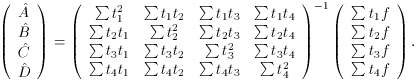
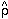 =
sqrt(
=
sqrt(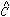 2 +
2 +
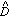 2) and
2) and
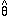 =
arctan(
=
arctan(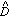 /
/
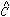 ) - no muss, no fuss, no
compromises, just good, clean least
squares straight from where you are to where you want to go.
) - no muss, no fuss, no
compromises, just good, clean least
squares straight from where you are to where you want to go.