6.1.3 Beamed LFs of High-Luminosity Radio Sources

The beaming calculation is as follows. We start with the derived parent luminosity function, then calculate the effect of beaming it [Eqs. (4)-(6)]) adjusting free parameters (the Lorentz factor) and f (the fraction of luminosity intrinsic to the jet) to match the observed luminosity function of FSRQ. It was not possible to fit the observed FSRQ luminosity function with a single Lorentz factor; it required instead a distribution in the range 5 40, weighted toward low values: n () ^-2.3, with a mean value < > 11 and f 5 x 10^-3. [Note that this last parameter is fixed by the largest and by the maximum value of the ratio between beamed and unbeamed radio flux, R; Eq. (C5).]

Figure 14 shows the beamed (solid line) and observed (filled circles) radio LFs of FSRQ, which are in very good agreement. The ratio between FSRQ and parents, integrated over the full luminosity function assuming that of the FR IIs cuts off at the low luminosity end, is ~ 2%. (Because of the flat LF slope at low luminosities, this percentage is not too sensitive to the cutoff.) The critical angle separating FSRQ from SSRQ and FR IIs ⁽¹⁵⁾ is _c(₁) ~ 14°. The fitted parameters of this beaming model are summarized in Table 3.

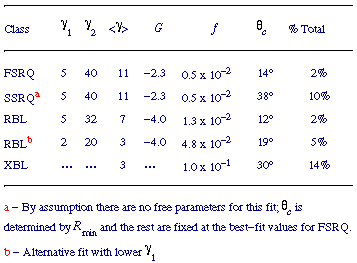
According to the beaming hypothesis, the steep-spectrum radio quasars are supposed to be at intermediate angles and their intrinsic properties - in particular, the value(s) of and f - must be identical to those of the FSRQ. Therefore, these parameters are already fixed. The method of calculation is similar to the one used in the previous section; however, since SSRQ are supposed to be misaligned objects, _min 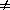0°. We take _min = 14°, and the observed value of R_min ~ 0.002 is used to constrain _max for SSRQ [Eq. (C4)]). With no free parameters, then, we calculate the beamed luminosity function of SSRQ.

The comparison between observations (open triangles) and the beaming model (dashed line) for SSRQ is shown in Fig. 14. The agreement is quite good, especially considering we did not adjust the parameters to optimize the FSRQ and SSRQ fits jointly. The angle dividing SSRQ from FR IIs is ~ 38° (Table 3).

The same distribution of Lorentz factors produces a good fit to both the luminosity functions of FSRQ and SSRQ. The value of ~ 38° for the angle separating SSRQ from FR II galaxies is in reasonable agreement with the angle derived from the number density ratio in the observed range of overlapping luminosity, = arccos (1 + 1/6.4)^-1 30°. The latter estimate is valid only when dealing with unbeamed luminosities or (in an approximate way) when the effect of beaming is not very strong because the objects are viewed off-axis, as in this case. For the 3CR sample, in which beaming is unimportant, Barthel (1989) found = 44°.4 from the ratio of quasars to radio galaxies in the interval 0.5 < z < 1.

Table 3 summarizes the beaming parameters for the radio band for different classes of objects (see Sec. 6.2 for a discussion of the parameters for the BL Lac class). Note that we have used p = 3 + (see Appendix B); using instead p = 2 + results in the Lorentz factors extending to higher values (Padovani and Urry 1992), and in a slightly larger critical angle.

From the observed values of R we can estimate a lower limit to the maximum Lorentz factor (Appendix C). The FR II galaxy OD -159 is the most lobe-dominated source in the 2 Jy sample. The most core-dominated FSRQ known is 0400+258, which does not actually belong to the 2 Jy sample (its 2.7 GHz flux ~ 1.5 Jy); its measured R is comparable to the lower limits (when no extended emission was detected) for some of the 2 Jy FSRQ. For these two objects, the R-values, K-corrected [Eq. (C2)] and extrapolated (when necessary) to 2.7 GHz rest frequency assuming _core - _ext = -1, are R_{min, FR IIs} < 6 x 10^-5 (OD -159; Morganti et al. 1993) and R_{max, FSRQ} 1000 (0400+258; Murphy et al. 1993). Using Eq. (C8), we find _max > (1.7 x 10⁷ 2^1-p)^1/2p ~ 13 for p = 3.

For these observed R values, small values of p imply high values for the largest Lorentz factor (here, for p = 2, _max 54). More precisely, _r -0.3 for the 2 Jy FSRQ (Padovani and Urry 1992) so p 1.7 - 2.7 if p ranges between 2 + and 3 + . Then _max 17 (for p = 2.7) or 120 (for p = 1.7). The need for quite high values of the largest s for smaller values of p was noted by Urry et al. (1991a) and Padovani and Urry (1992) from their fits to the observed LFs.

While the SSRQ-FSRQ-only scheme (ignoring the radio galaxies; Orr and Browne 1982) can not be ruled out, it is much harder to reconcile with the available data, mainly because there seem to be too few SSRQ for them to be the parents of FSRQ (Padovani and Urry 1992). The FR II-SSRQ-FSRQ scheme, illustrated by the curves in Fig. 14, can be tested further via the predicted radio counts of flat- and steep-spectrum quasars, which converge at easily accessible levels (Padovani and Urry 1992).