


The calculations that led to equation (51) are accurate to the appropriate order in photon frequency and electron energy for our purposes, and take account of the relativistic kinematics and statistics of the scattering process. In the non-relativistic limit the scattering process simplifies substantially, and may be described by the Kompaneets (1956) equation
which describes the change in the occupation number, n(
is a dimensionless measure of time spent in the electron
distribution. (4)
Note that a time- (or y-) independent solution of
(52) is given when the
electrons and photons are in thermal equilibrium, so that
n = (exe -1 )-1,
as expected, and that the more general
Bose-Einstein distributions n =
(exe+
In the limit
of small xe, which is certainly appropriate for the
CMBR and hot electrons, ð n / ð xe
>> n, n2, and
(52) becomes
The homogeneity of the right hand side of this equation allows us to
replace xe by x, and a change of variables from
x, y to
In the format of equation (49), this indicates
that the solution of the Kompaneets equation can be written
where the Kompaneets scattering kernel is of Gaussian form
(Sunyaev 1980;
Bernstein & Dodelson
1990).
The difference between the
scattering kernels (33) and (58) is
small but significant for the mildly
relativistic electrons that are important in most cases, and can
become large where the electron distribution becomes more relativistic
(compare the solid and dashed lines in
Fig. 5).
These shape changes lead to spectral differences
in the predicted
Most work on the Sunyaev-Zel'dovich effect has used the Kompaneets
equation, and implicitly the Kompaneets scattering kernel, rather than
the more precise relativistic kernel (44) advocated by
Rephaeli (1995a).
The two kernels are the same at small Te, as expected
since the Kompaneets equation is correct in the low-energy limit. At
low optical depth and low temperatures, where the
Comptonization parameter y is small, and for
an incident photon spectrum of the form of equation (15),
the approximation
ð n / ð y =
with a corresponding
There are three principal simplifications gained by using
(59), rather than the relativistic results.
as seen in Fig. 9. Earlier approximations for
xzero(
It is possible to improve on the Kompaneets result
(59) by working to higher order in 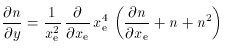
 ) by a
diffusion process. In (52), xe = h
) by a
diffusion process. In (52), xe = h  /
kB Te, which should not be confused
with x = h
/
kB Te, which should not be confused
with x = h  / kB
Trad used previously, and
/ kB
Trad used previously, and
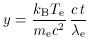
 e is the ``Compton
range'', or the
scattering mean free path, (ne
e is the ``Compton
range'', or the
scattering mean free path, (ne  T)-1.
For a radiation field passing though an electron cloud, y, which is
usually known as the Comptonization parameter, can be
rewritten in the more usual form
T)-1.
For a radiation field passing though an electron cloud, y, which is
usually known as the Comptonization parameter, can be
rewritten in the more usual form
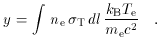
 -1)-1 are also
solutions. A derivation of equation (52) from the
Boltzmann equation is given by
Bernstein & Dodelson
(1990).
-1)-1 are also
solutions. A derivation of equation (52) from the
Boltzmann equation is given by
Bernstein & Dodelson
(1990).
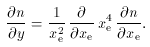
 ,
y, where
,
y, where  =
3y + ln xe, reduces (55) to
the canonical form of the diffusion equation,
=
3y + ln xe, reduces (55) to
the canonical form of the diffusion equation,
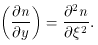
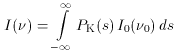
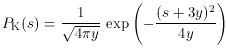
 I (
I ( ),
which for thermal electrons can be characterized by the changing
positions of the minimum, zero, and maximum of the spectrum of the
Sunyaev-Zel'dovich effect with changing electron temperature. This is
illustrated in
Fig. 9 for a range of temperatures that is of most
interest for the clusters of galaxies
(Section 4).
),
which for thermal electrons can be characterized by the changing
positions of the minimum, zero, and maximum of the spectrum of the
Sunyaev-Zel'dovich effect with changing electron temperature. This is
illustrated in
Fig. 9 for a range of temperatures that is of most
interest for the clusters of galaxies
(Section 4).
 n / y may be used in
(55) to obtain a simple form for the spectral
change caused by scattering
n / y may be used in
(55) to obtain a simple form for the spectral
change caused by scattering
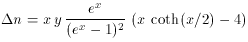
 I
(x) = x3
I
(x) = x3  n (x) I0, where
I0 = 2 h / c2
[(kB Trad / h)]3 again.
This result can also be obtained directly from the integral
(57) for I (x) in the limit of small
y. Fig. 7
compares the Kompaneets approximation for
n (x) I0, where
I0 = 2 h / c2
[(kB Trad / h)]3 again.
This result can also be obtained directly from the integral
(57) for I (x) in the limit of small
y. Fig. 7
compares the Kompaneets approximation for
 I (x) with the full
relativistic results.
I (x) with the full
relativistic results.
1.
The spectrum of the effect is given by a simple analytical
function (59).
2.
The location of the spectral maxima, minima, and zeros are
independent of Te in the Kompaneets approximation, but
vary with Te in the relativistic expressions. To first
order in  ,
which is adequate for temperatures kB
Te < 20 keV (
,
which is adequate for temperatures kB
Te < 20 keV ( < 0.04),
< 0.04),
 )
)
 )
)
 ) are
given by
Fabbri (1981) and
Rephaeli (1995a).
) are
given by
Fabbri (1981) and
Rephaeli (1995a).
3.
The amplitude of the intensity (or brightness temperature)
change depends only on y (  Te
Te  e)
in the Kompaneets approximation, but in the
relativistic expression the amplitude is proportional to
e)
in the Kompaneets approximation, but in the
relativistic expression the amplitude is proportional to
 e (for small
e (for small  e) and also depends on a
complicated function of Te.
e) and also depends on a
complicated function of Te.
 from (51) or the Boltzmann equation. The
resulting expressions for
from (51) or the Boltzmann equation. The
resulting expressions for  n or
n or  I are
usually written as a series in increasing powers of
I are
usually written as a series in increasing powers of  (Challinor & Lasenby
1998;
Itoh et al. 1998;
Stebbins 1998).
Taken to four or
five terms these series provide a useful analytical expression for the
Sunyaev-Zel'dovich effect for hot clusters for a wide range of
x. However, the expressions cannot be used blindly since they are
asymptotic approximations, and are still of poor accuracy for some
(x,
(Challinor & Lasenby
1998;
Itoh et al. 1998;
Stebbins 1998).
Taken to four or
five terms these series provide a useful analytical expression for the
Sunyaev-Zel'dovich effect for hot clusters for a wide range of
x. However, the expressions cannot be used blindly since they are
asymptotic approximations, and are still of poor accuracy for some
(x,  ) values. The
approximations also rely on the assumptions
that the cluster is optically thin and that the electron distribution
function is that of a single-temperature gas (35). Both
assumptions are questionable when precise results (to better than
1 per cent) are needed, and so the utility of the idealized multi-term
expressions is limited. For the most precise work, especially work on
the kinematic Sunyaev-Zel'dovich effect (Section 6),
the relativistic expressions with suitable forms for the distribution
functions, and proper treatment of the cluster optical depth, must be
used if accurate spectra for the effect, and hence estimates for the
cluster velocities, are to be obtained
(Molnar & Birkinshaw
1998b).
) values. The
approximations also rely on the assumptions
that the cluster is optically thin and that the electron distribution
function is that of a single-temperature gas (35). Both
assumptions are questionable when precise results (to better than
1 per cent) are needed, and so the utility of the idealized multi-term
expressions is limited. For the most precise work, especially work on
the kinematic Sunyaev-Zel'dovich effect (Section 6),
the relativistic expressions with suitable forms for the distribution
functions, and proper treatment of the cluster optical depth, must be
used if accurate spectra for the effect, and hence estimates for the
cluster velocities, are to be obtained
(Molnar & Birkinshaw
1998b).
4 (53) corrects equation (11) in
the Kompaneets paper for an obvious typographical error.
Back.