


Although early work on the Sunyaev-Zel'dovich effects concentrated on the
thermal effect, a second effect must also occur when
the thermal (or non-thermal) Sunyaev-Zel'dovich effect is present. This is the
velocity (or kinematic) Sunyaev-Zel'dovich effect, which
arises if the scattering medium causing the thermal (or non-thermal)
Sunyaev-Zel'dovich effect is moving relative to the Hubble
flow. In the reference frame of the scattering gas the microwave background
radiation appears anisotropic, and the effect of the inverse-Compton
scattering is to re-isotropize the radiation slightly. Back in the
rest frame of the observer the radiation field is no longer
isotropic, but shows a structure towards the scattering atmosphere
with amplitude proportional to  e vz / c, where
vz is the component of peculiar velocity of the scattering
atmosphere along the line of sight
(Sunyaev & Zel'dovich
1972;
Rephaeli & Lahav 1991).
e vz / c, where
vz is the component of peculiar velocity of the scattering
atmosphere along the line of sight
(Sunyaev & Zel'dovich
1972;
Rephaeli & Lahav 1991).
The most interesting aspect of the kinematic effect is that it provides a method for measuring one component of the peculiar velocity of an object at large distance, provided that the velocity and thermal effects can be separated, as they can using their different spectral properties. Since there is evidence for large-scale motions of clusters of galaxies in the local Universe, both from COBE (Fixsen et al. 1996) and from direct observations of galaxies (e.g., Dressler et al. 1987; Lynden-Bell et al. 1988), and these motions place strong constraints on the dynamics of structure formation (see the review of Davis et al. 1992), other examples of large-scale flows would be of considerable interest. This is particularly true if those flows can be measured over a range of redshifts, so that the development of the peculiar velocity field can be studied. At present this is beyond the capability of the measurements (Sec. 8), but rapid progress is being made in this area.
Even larger velocities are possible for scattering gas: radio source lobes may be moving at speeds that approach the speed of light, and expanding at hundreds or thousands of km s-1. Although this will boost the kinematic effect, the optical depths of these lobes are probably too small to make the effect observable at present (Sec. 5; Molnar 1998).
Although Sunyaev & Zel'dovich (1972) quoted the result that the radiation temperature decrease in the kinematic effect is
and the spectrum of the kinematic effect has often been quoted (e.g.,
by
Rephaeli 1995b),
the first published derivation of
the size and spectrum of the kinematic effect was given by
Phillips (1995).
The version of the derivation given
here is similar to Phillips' argument, but uses different conventions
and the radiative transfer equation (19) rather than
the Boltzmann equation.
For the sake of simplicity, it is assumed that the kinematic and the
thermal effects are both small, and that only single scatterings are
important. Then the thermal effect, which depends on random motions of
the scattering electrons, and the kinematic effect, which depends on their
systematic motion, will decouple and we can derive the kinematic
effect by taking the electrons to be at rest in the frame of the
scattering medium. This approximation will ignore quantities which
involve cross-products
[(kB Te) / (me
c2)] (vz /
c) relative to terms of order
[(kB Te) / (me
c2)] and (vz / c).
Since the peculiar velocities and electron temperatures are
small for the thermal Sunyaev-Zel'dovich effect, this will not be a
significant limitation on the result for clusters of galaxies. However, this
approximation is not valid for the non-thermal effect, where electron
energies >> me c2 are likely, and an alternative
analysis is necessary
(Molnar 1998;
Nozawa et al. 1998).
In the rest frame of the CMBR, the spectrum of the radiation follows
(1), and the occupation number has the form
(15). The occupation number in mode
where x1 = (h
We may apply the Boltzmann equation (e.g., as in
Peebles 1993,
Sec. 24 and
Phillips 1995),
or the radiative transfer equation (19), to
derive an equation for the scattered radiation intensity. Using
(19), and the form (24) for the scattering redistribution function, the
specific intensity is given by
The optical depth,
where the optical depth is now inserted as an explicit argument of
I. For µ = 1, the
scattering redistribution function takes a particularly simple form,
and we can write the fractional
change in the specific intensity in the frame of the scattering gas
as
The expression on the left-hand side of this equation is a
relativistic invariant: the same fractional
intensity change would seen by an observer in the rest frame of the
CMBR at frequency
where
x2 = x
For small
so that the changes in specific intensity and brightness temperature
are given by
This spectral form corresponds to a simple decrease in the radiation
temperature (79), as stated by
Sunyaev & Zel'dovich
(1972).
For the cluster CL 0016+16 discussed in
Sec. 4, the
X-ray data imply a central scattering optical depth
It would be very difficult to locate the kinematic Sunyaev-Zel'dovich
effect in the presence of the thermal Sunyaev-Zel'dovich effect at low
frequency. The ratio of the brightness temperature changes caused by the
effects is
which is small for the expected velocities of a few hundred km
s-1 or
less, and typical cluster temperatures of a few keV. However, the
thermal and kinematic effects may be separated using their different
spectra: indeed, in the Kompaneets approximation it is easy to show
that the kinematic effect produces its maximum intensity
change at the frequency at which the thermal effect is zero.
Thus observations near x = 3.83 (218 GHz) are sensitive mostly to the
kinematic effect, but in interpreting such observations it is necessary
to take careful account
of the temperature-dependence of the shape of the thermal Sunyaev-Zel'dovich
effect's spectrum, and of the frequency of the
null of the thermal effect (Equation 60;
Fig. 9), as emphasized by
Rephaeli (1995a).
The first strong limits on the
peculiar velocities of clusters of galaxies derived using this
technique are now becoming available (e.g.,
Holzapfel et
al. 1997b;
see Sec. 10.2).
Although this technique measures only the peculiar radial velocity of
a cluster of galaxies, the other velocity components may be measured
using the specific intensity changes caused by gravitational lensing
(e.g.,
Birkinshaw & Gull 1983a,
corrected by
Gurvits & Mitrofanov
1986;
Pyne & Birkinshaw 1993).
These fractional intensity changes are
small, of order
Clusters of galaxies produce further microwave background anisotropies
through the same spacetime effect, if they are expanding or contracting
(Nottale 1984;
Pyne & Birkinshaw 1993).
A contaminating Sunyaev-Zel'dovich effect must also appear at the
same time
if an expanding or collapsing cluster contains associated gas because
of the anisotropy of inverse-Compton scattering
(Molnar & Birkinshaw
1998b),
but the sizes of these effects are
too small to be detectable in the near future.
An interesting extension of this work would be to use the kinematic
Sunyaev-Zel'dovich effect from a radio source to measure the speed of the
radio-emitting plasma. Just as for a cluster of galaxies, the presence
of a scattering medium which is moving relative to the CMBR will
produce a kinematic Sunyaev-Zel'dovich effect which is proportional to

 in a frame moving at speed vz along the z axis away
from the observer is then
in a frame moving at speed vz along the z axis away
from the observer is then

 1) / (kB T1)
is the dimensionless frequency of photons in the frame of
the scattering medium, the radiation temperature of the CMBR as seen
by an observer at rest in the Hubble flow near the scattering gas is
T1 = Trad (1 +
zH), zH is the Hubble flow
redshift, and
1) / (kB T1)
is the dimensionless frequency of photons in the frame of
the scattering medium, the radiation temperature of the CMBR as seen
by an observer at rest in the Hubble flow near the scattering gas is
T1 = Trad (1 +
zH), zH is the Hubble flow
redshift, and  z = vz / c measures
the peculiar
velocity.
z = vz / c measures
the peculiar
velocity.  z is the corresponding Lorentz
factor. µ1 = cos
z is the corresponding Lorentz
factor. µ1 = cos 1 is the
direction cosine of photons arriving at a scattering electron,
relative to the z axis and measured in the frame of the moving
scattering medium (Fig. 12). The relativistic
transformation of frequency relates
1 is the
direction cosine of photons arriving at a scattering electron,
relative to the z axis and measured in the frame of the moving
scattering medium (Fig. 12). The relativistic
transformation of frequency relates  1 to
1 to  in the
frame at rest
relative to the CMBR by
in the
frame at rest
relative to the CMBR by  1
=
1
=  z ( 1
+
z ( 1
+  z)
z)  ,
since the observer at rest sees the scattered photons along the z
axis, where µ = cos
,
since the observer at rest sees the scattered photons along the z
axis, where µ = cos = 1.
= 1.
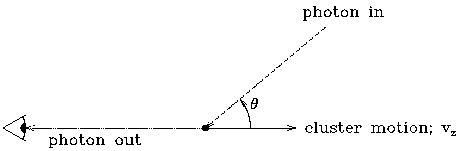
Figure 12. The geometry for the discussion of the
kinematic Sunyaev-Zel'dovich effect, as seen in the frame of an observer
at rest in the Hubble flow.

 e,
enters from (19) as
e,
enters from (19) as
 e =
e = 

 ,sca dz.
For small optical depth, so that photons are scattered only once, this
can be simplified to
,sca dz.
For small optical depth, so that photons are scattered only once, this
can be simplified to


 , where
, where  is related to
is related to  1 by a Lorentz
transform. Furthermore, this is also the fractional intensity change
seen by a distant observer, for whom the scattering medium lies at redshift
zH, after allowance is made for the redshifting of frequency
and radiation temperature. Using the expression for n
1 by a Lorentz
transform. Furthermore, this is also the fractional intensity change
seen by a distant observer, for whom the scattering medium lies at redshift
zH, after allowance is made for the redshifting of frequency
and radiation temperature. Using the expression for n in
(80), and working in terms of the frequency seen at
redshift zero,
in
(80), and working in terms of the frequency seen at
redshift zero,  , (83) becomes
, (83) becomes

 z2 (1 +
z2 (1 +  z) ( 1 -
z) ( 1 -  z
µ1) and x = (h
z
µ1) and x = (h  ) / (kB Trad) as usual.
) / (kB Trad) as usual.
 z, the integral can be expanded in powers of
z, the integral can be expanded in powers of
 z, and
the symmetry of the integrand ensures that only
terms in the expansion which are even powers of
µ1 will appear in
the result. This enables the integral to be performed easily, giving
the result
z, and
the symmetry of the integrand ensures that only
terms in the expansion which are even powers of
µ1 will appear in
the result. This enables the integral to be performed easily, giving
the result



 e0 = 0.01
h100-1/2. At low
frequency the brightness
temperature change through the cluster center caused by the kinematic
effect is -
e0 = 0.01
h100-1/2. At low
frequency the brightness
temperature change through the cluster center caused by the kinematic
effect is -  e0
(vz / c) Trad
= - 0.1 (vz / 1000 km s-1)
h100-1/2 mK,
significantly less than the central thermal Sunyaev-Zel'dovich effect of
-0.82 h100-1/2 mK for all likely
vz.
e0
(vz / c) Trad
= - 0.1 (vz / 1000 km s-1)
h100-1/2 mK,
significantly less than the central thermal Sunyaev-Zel'dovich effect of
-0.82 h100-1/2 mK for all likely
vz.

 grav
(vxy / c), where
grav
(vxy / c), where
 grav is the
gravitational lensing angle, and
vxy is the velocity of the cluster across the
observer's line of sight.
(6) For
typical cluster masses and sizes, the gravitational
lensing angle is less than about 1 arcmin, so that
(
grav is the
gravitational lensing angle, and
vxy is the velocity of the cluster across the
observer's line of sight.
(6) For
typical cluster masses and sizes, the gravitational
lensing angle is less than about 1 arcmin, so that
( I / I)
I / I)  10-6
(vxy/1000 km s-1),
whereas the kinematic Sunyaev-Zel'dovich effect may be an order of magnitude
stronger. The possibility of measuring vz and
vxy
separately then depends on the different angular patterns of the
effects on the sky: the transverse motion produces a characteristic
dipole-like effect near the moving cluster, with an angular structure
which indicates the direction of motion on the plane of the
sky. Nevertheless, substantial improvements in techniques are going to
be required to measure these other velocity terms in this way.
10-6
(vxy/1000 km s-1),
whereas the kinematic Sunyaev-Zel'dovich effect may be an order of magnitude
stronger. The possibility of measuring vz and
vxy
separately then depends on the different angular patterns of the
effects on the sky: the transverse motion produces a characteristic
dipole-like effect near the moving cluster, with an angular structure
which indicates the direction of motion on the plane of the
sky. Nevertheless, substantial improvements in techniques are going to
be required to measure these other velocity terms in this way.
 e
(vz / c), but whereas vz should be
small for a cluster
relative to the Hubble flow, the velocity of the radio-emitting plasma
in a radio galaxy may be a substantial fraction of the speed of
light, and a large kinematic Sunyaev-Zel'dovich effect will be seen if
the optical
depth of the radio-emitting plasma is sufficient. A complication here
is that the location of the null of the non-thermal Sunyaev-Zel'dovich effect
depends on the spectrum of the electrons, and that the cross-terms
between the electron energy and the plasma velocity are no longer
small. Thus the approximation of a cold plasma that was made in the
derivation above, to calculate the spectrum of the kinematic
Sunyaev-Zel'dovich
effect, is no longer valid and a more complete calculation must be
performed using proper angular averages over the (anisotropic)
electron distribution function (see
Molnar 1998).
e
(vz / c), but whereas vz should be
small for a cluster
relative to the Hubble flow, the velocity of the radio-emitting plasma
in a radio galaxy may be a substantial fraction of the speed of
light, and a large kinematic Sunyaev-Zel'dovich effect will be seen if
the optical
depth of the radio-emitting plasma is sufficient. A complication here
is that the location of the null of the non-thermal Sunyaev-Zel'dovich effect
depends on the spectrum of the electrons, and that the cross-terms
between the electron energy and the plasma velocity are no longer
small. Thus the approximation of a cold plasma that was made in the
derivation above, to calculate the spectrum of the kinematic
Sunyaev-Zel'dovich
effect, is no longer valid and a more complete calculation must be
performed using proper angular averages over the (anisotropic)
electron distribution function (see
Molnar 1998).
6 This is a special case of a more
general class of
intensity-changing effects, often referred to as Rees-Sciama effects
(after
Rees & Sciama 1968),
which arise when the
evolution of spacetime near a cluster (or other massive object)
differs from the evolution of the metric of the Universe as a whole
(Pyne & Birkinshaw
1993).
Back.