


The results in Section 3 indicate that passage of radiation through an electron population with significant energy content will produce a distortion of the radiation's spectrum. In the present section the question of the effect of thermal electrons on the CMBR is addressed in terms of the three likely sites for such a distortion to occur:
| 1. | the atmospheres of clusters of galaxies |
| 2. | the ionized content of the Universe as a whole, and |
| 3. | ionized gas close to us. |
4.1.
The Sunyaev-Zel'dovich effect from clusters of
galaxies
By far the commonest references to the Sunyaev-Zel'dovich effect in the literature are to the effect that the atmosphere of a cluster of galaxies has on the CMBR. Cluster atmospheres are usually detected through their X-ray emission, as in the example shown in Fig. 2, although the existence of such gas can also be inferred from its effects on radio source morphologies (e.g., Burns & Balonek 1982) - `disturbed' lobe shapes and head-tail sources being typical indicators of the presence of cluster gas.
If a cluster atmosphere contains gas with electron concentration ne (r), then the scattering optical depth, Comptonization parameter, and X-ray spectral surface brightness along a particular line of sight are
where z is the redshift of the cluster, and
By far the most detailed information on the structures of cluster
atmospheres is obtained from X-ray astronomy satellites, such as
ROSAT and ASCA. Even though these satellites also provide some
information about the spectrum of
bX (and hence an emission-weighted measure of the average gas
temperature along the line of sight) there is no unique inversion of
(63) to ne (r) and Te
(r).
Thus it is not possible to predict accurately the distribution of y
on the sky, and hence the shape of the Sunyaev-Zel'dovich effect
(which we will, in the current section, take to be close to the shape
of y, although Sec. 3.3 indicates that an
accurate prediction of the Sunyaev-Zel'dovich effect requires a
more complicated calculation which includes both the electron
scattering optical depth and the gas temperature).
In many cases it is then convenient to introduce a parameterized model
for the properties of the scattering gas in the cluster, and to fit the
the values of these parameters to the X-ray data. The integral (62)
can then be performed to predict the appearance of the cluster in the
Sunyaev-Zel'dovich effect. A form that is convenient, simple, and
popular is the isothermal
(Cavaliere &
Fusco-Femiano 1976,
1978:
the so-called `isothermal beta model'). This has been much used to fit
the X-ray structures of clusters of galaxies and individual galaxies
(see the review of
Sarazin 1988).
Under these assumptions the cluster will produce circularly-symmetrical
patterns of scattering optical depth, Comptonization parameter and X-ray
emission, with
where the central values are
if the cosmological constant is taken to be zero (as it is throughout
this review).
A useful variation on this model was introduced by
Hughes et
al.(1988)
on the basis of observations of the Coma cluster. Here the divergence in gas mass which
arises for typical
values of
where rlim is the limiting gas radius,
riso is the
isothermal radius, and
For cluster CL 0016+16 shown in
Fig. 2, the redshift
of 0.5455 implies an angular diameter distance DA = 760
h100-1 Mpc (for q0 =
0.5). The X-ray emission mapped with the
ROSAT PSPC best matches a circular distribution of form
(67) with structural parameters
Using the known response of the ROSAT PSPC and the spectral
parameters of the X-ray emission found from the ASCA data,
the emissivity of the intracluster gas in CL 0016+16 is
More complicated models of the cluster density and temperature can be
handled either analytically, or by numerical integrations. For
example, Fig. 2 clearly shows a
non-circular structure
for CL 0016+16: a better representation of the structure of the
atmosphere may then be to replace (64) by an ellipsoidal
model, with
where the matrix M encodes the orientation and relative sizes
of the semi-major axes of the cluster. If CL 0016+16 is assumed to be
intrinsically oblate, with its symmetry axis in the plane of the sky
(at position angle
Whether (64) or (74) is used to describe
the density structure of a cluster, it is important to be aware that
these representations are not directly tied to physical descriptions
of the gas physics and mass distribution in real clusters, but simply
choices of convenience. In principle a comparison of the
Sunyaev-Zel'dovich effect
map and X-ray image of a cluster could be used to derive interesting
information about the structure of the gas, particularly when combined
with other information on cluster structure, such as weak lensing maps
of the cluster mass distribution, velocity dispersion measurements,
and data on the locations of cluster galaxies. Even based on the X-ray
and Sunyaev-Zel'dovich effect data alone there are several possibilities
for finding out more about cluster structures.
However, most of the recent interest in the Sunyaev-Zel'dovich effects
of clusters has not been because of their use as diagnostics of the cluster
atmospheres, but rather because the effects can be used as
cosmological probes. A detailed explanation of the method and its
limitations is given in Section 11, but the
essence of the method is a comparison of the Sunyaev-Zel'dovich effect
predicted from the X-ray
data with the measured effect. Since the predicted effect is
proportional to h100-1/2 via the
dependence on the angular
diameter distance (equation 68 with rc =
DA
It should be emphasized that the
Sunyaev-Zel'dovich effect has the unusual property of being redshift
independent:
the effect of a cluster is to cause some
fractional change in the brightness of the CMBR, and this fractional
change is then seen at all positions on the line of sight through the
cluster, at whatever redshift. Thus the central Sunyaev-Zel'dovich
effect through a cluster with the properties of CL 0016+16 will have the
same value whether the cluster is at redshift 0.55, 0.055, or 5.5. This
makes the Sunyaev-Zel'dovich effect exceptionally valuable as a
cosmological probe of hot electrons, since it should be detectable at
any redshift for which regions with large electron pressures exist.
There have now been a number of detections of the Sunyaev-Zel'dovich
effects of clusters, and recent improvements in the sensitivities of
interferometers with modest baselines have led to many maps of the
effects. A discussion of the detection strategies, and the
difficulties involved in comparing the results from different
instruments, is given in Section 8.
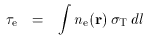
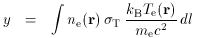
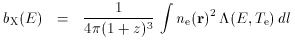
 is the
spectral emissivity of the gas at observed X-ray energy E or into some
bandpass centered on energy E (including both line and continuum
processes). The factor of 4
is the
spectral emissivity of the gas at observed X-ray energy E or into some
bandpass centered on energy E (including both line and continuum
processes). The factor of 4 in the
expression for bX
arises from the assumption that this emissivity is
isotropic, while the (1 + z)3 factor takes account of the
cosmological transformations of spectral surface brightness and
energy.
in the
expression for bX
arises from the assumption that this emissivity is
isotropic, while the (1 + z)3 factor takes account of the
cosmological transformations of spectral surface brightness and
energy.
 model, where it is assumed that the
electron temperature Te is constant and that the
electron number density follows the spherical distribution
model, where it is assumed that the
electron temperature Te is constant and that the
electron number density follows the spherical distribution
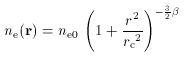
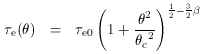


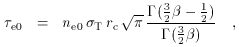
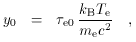
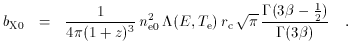
 is the angle between the
center of the cluster and the
direction of interest and
is the angle between the
center of the cluster and the
direction of interest and  c = rc / DA
is the angular core radius of the cluster as deduced from
the X-ray data. DA is the angular diameter distance of the
cluster, given in terms of redshift, deceleration parameter
q0 , and Hubble constant by
c = rc / DA
is the angular core radius of the cluster as deduced from
the X-ray data. DA is the angular diameter distance of the
cluster, given in terms of redshift, deceleration parameter
q0 , and Hubble constant by
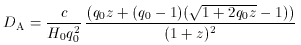
 that fit
X-ray images is eliminated by truncating
the electron density distribution. A model structure of similar form
describes the decrease of gas temperature at large radius. The
density and temperature functions used are
that fit
X-ray images is eliminated by truncating
the electron density distribution. A model structure of similar form
describes the decrease of gas temperature at large radius. The
density and temperature functions used are
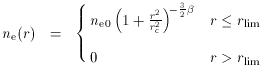
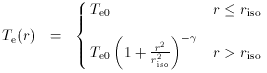
 is some index. Not all choices of
these parameters are physically reasonable, but the forms above
provide an adequate description of at least some cluster structures.
Further modifications of models (72 - 73)
are required in cases where the cluster displays a cooling flow
(Fabian et al. 1984),
but this will be
important only in Sec. 11.1 in the present review.
is some index. Not all choices of
these parameters are physically reasonable, but the forms above
provide an adequate description of at least some cluster structures.
Further modifications of models (72 - 73)
are required in cases where the cluster displays a cooling flow
(Fabian et al. 1984),
but this will be
important only in Sec. 11.1 in the present review.
 = 0.73 ± 0.02
and
= 0.73 ± 0.02
and  c = 0.69 ±
0.04 arcmin, so that rc = (150 ±
10)h100-1 kpc. The corresponding cluster
central X-ray
brightness, b0 = 0.047 ± 0.002 counts s-1
arcmin-2
(Hughes & Birkinshaw
1998).
X-ray spectroscopy of the cluster using data from the GIS on the ASCA
satellite and the ROSAT PSPC led to a gas temperature
kBTe = 7.6
± 0.6 keV and a metal abundance in the cluster that is only 0.07
solar. The X-ray spectrum is absorbed by a line-of-sight column with
equivalent neutral hydrogen column density NH = (5.6
± 0.4) x 1020 cm-2. These spectral parameters are
consistent with the results obtained by Yamashita
(1994) using the ASCA data alone.
(5)
c = 0.69 ±
0.04 arcmin, so that rc = (150 ±
10)h100-1 kpc. The corresponding cluster
central X-ray
brightness, b0 = 0.047 ± 0.002 counts s-1
arcmin-2
(Hughes & Birkinshaw
1998).
X-ray spectroscopy of the cluster using data from the GIS on the ASCA
satellite and the ROSAT PSPC led to a gas temperature
kBTe = 7.6
± 0.6 keV and a metal abundance in the cluster that is only 0.07
solar. The X-ray spectrum is absorbed by a line-of-sight column with
equivalent neutral hydrogen column density NH = (5.6
± 0.4) x 1020 cm-2. These spectral parameters are
consistent with the results obtained by Yamashita
(1994) using the ASCA data alone.
(5)
 e0 = (2.70 ± 0.06)
x 10-13 counts s-1 cm-5. The central
electron number density can then be found from (70) to be about
1.2 x 10-2 h1001/2 electrons
cm-3.
The corresponding central optical depth through the cluster is
e0 = (2.70 ± 0.06)
x 10-13 counts s-1 cm-5. The central
electron number density can then be found from (70) to be about
1.2 x 10-2 h1001/2 electrons
cm-3.
The corresponding central optical depth through the cluster is
 e0 = 0.01
h100-1/2, which
corresponds to a central Comptonization parameter y0 = 1.5 x
10-4h100-1/2. At such a small
optical depth, the Sunyaev-Zel'dovich
effect through the cluster should be well described by
(51), so that the brightness change through the cluster center should be
e0 = 0.01
h100-1/2, which
corresponds to a central Comptonization parameter y0 = 1.5 x
10-4h100-1/2. At such a small
optical depth, the Sunyaev-Zel'dovich
effect through the cluster should be well described by
(51), so that the brightness change through the cluster center should be
 T0 =
-2y0Trad
T0 =
-2y0Trad  -0.82
h100-1/2 mK at low frequency.
-0.82
h100-1/2 mK at low frequency.
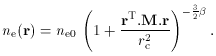
 -40°) and with structural parameters
that match the X-ray image, then the intrinsic axial ratio is 1.17
± 0.03, with best-fitting values for
-40°) and with structural parameters
that match the X-ray image, then the intrinsic axial ratio is 1.17
± 0.03, with best-fitting values for  and the major axis
core radius of 0.751 ± 0.025 and 0.763 ± 0.045 arcmin
(Hughes & Birkinshaw
1998).
The central X-ray surface
brightness is almost unchanged, reflecting the good degree of
resolution of the cluster structure effected by the ROSAT PSPC. With
these structural parameters, the predicted Sunyaev-Zel'dovich effect map of the
cluster is as shown in Fig. 10. The predicted central
Sunyaev-Zel'dovich effect is now
and the major axis
core radius of 0.751 ± 0.025 and 0.763 ± 0.045 arcmin
(Hughes & Birkinshaw
1998).
The central X-ray surface
brightness is almost unchanged, reflecting the good degree of
resolution of the cluster structure effected by the ROSAT PSPC. With
these structural parameters, the predicted Sunyaev-Zel'dovich effect map of the
cluster is as shown in Fig. 10. The predicted central
Sunyaev-Zel'dovich effect is now  T0
T0  -0.84h100-1/2 mK at low
frequency, very little changed from the prediction of the circular model.
-0.84h100-1/2 mK at low
frequency, very little changed from the prediction of the circular model.
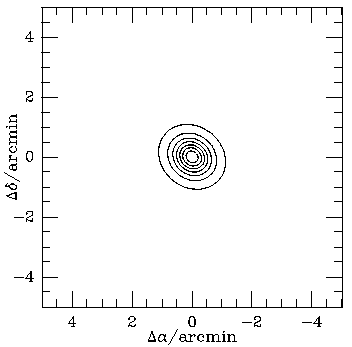
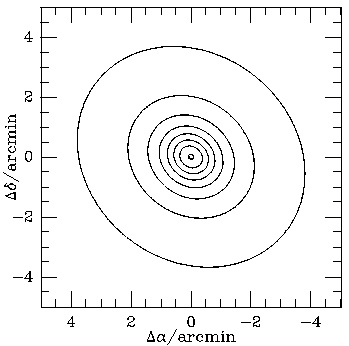
Figure 10. A model for CL 0016+16
assuming that the cluster is oblate with the symmetry axis
in the plane of the sky, and with the structural parameters
fixed by fits to the ROSAT PSPC image
(Fig. 2). Left: the model X-ray
surface brightness. Right: the model Sunyaev-Zel'dovich effect.
The contours in both plots are spaced at
intervals of 12.5 per cent of the peak effect - note that the
Sunyaev-Zel'dovich effect shows a much greater angular extent than the X-ray
emission (compare the angular dependences in equations 66 and 67.
The central Sunyaev-Zel'dovich effect predicted on the basis of the X-ray data
is -0.84h100-1/2 mK.
1.
A comparison of the Sunyaev-Zel'dovich and X-ray images might be
used to determine the intrinsic three-dimensional shape of the
cluster. However, the leverage that the data have
on the three-dimensional projection is poor. Changing the
model for CL 0016+16 from oblate to prolate only results in a change
of about 9 per cent in the central predicted Sunyaev-Zel'dovich
effect. Thus this is unlikely to be a useful tool, at least for simple
X-ray structures.
2.
Since the X-ray emission depends on some average of
ne2 along the line of sight, while the
Sunyaev-Zel'dovich effect depends on an average of ne,
the shape of the Sunyaev-Zel'dovich effect image that is predicted
is sensitive to variations of the clumping factor
Cn = < ne2 >
/ < ne > 2 on the different lines of
sight through the cluster if clumping occurs at constant gas
temperature. The amplitude of the Sunyaev-Zel'dovich effect, indeed,
scales as sqrt (Cn). Thus it might be possible to
measure the sub-beam scale clumping in the cluster gas. However, if
the clumping occurs with a compensating temperature change then the
effect may be reduced. For example, if the X-ray emissivity is
proportional to Te-1/2 and the clumping is
adiabatic, then
changes in the X-ray emissivity are matched by equal changes in the
Comptonization parameter and no difference will be seen in the
Sunyaev-Zel'dovich effect image predicted based on the X-ray data.
3.
Probably the most useful astrophysical result that can be
extracted from the comparison is information on
thermal structure in the intracluster gas. The X-ray and
Sunyaev-Zel'dovich effect images depend on Te in different
ways, with the X-ray image from a particular satellite being a
complicated function of temperature, while the Sunyaev-Zel'dovich
effect image is close to being an image
of the electron pressure. A comparison of the two images therefore
gives information about thermal structure - particularly the thermal
structure of the outer part of the cluster, which has a greater
fractional contribution to the Sunyaev-Zel'dovich effect than to the
X-ray emission (since the X-ray emission depends on
ne2 while
the Sunyaev-Zel'dovich effect depends on ne). However, it is
likely that this information will be more easily gained using
spatially-resolved spectroscopy on the next generation of X-ray satellites.
4.
Finally, as has been emphasized by
Myers et al.
(1997),
the Sunyaev-Zel'dovich effect is a direct measure of the
projected mass of gas in the cluster on the line of sight if the
temperature structure of the cluster is simple. This implies that the
baryonic surface mass density in the cluster can be measured directly,
and compared with other measurements of the mass density, for example
from gravitational lensing. A discussion of this in relation to the
cluster baryon problem appears in Section 10.
 c; see also the
discussion of CL 0016+16 above), this comparison
measures the value of the Hubble constant, and potentially other
cosmological parameters.
c; see also the
discussion of CL 0016+16 above), this comparison
measures the value of the Hubble constant, and potentially other
cosmological parameters.
5 In this section all errors
given in
Hughes & Birkinshaw
(1998)
have been converted to symmetrical ± 1 errors, for simplicity. Better
treatments of the errors are used in more critical calculations, for
example in Sec. 11. Back.
errors, for simplicity. Better
treatments of the errors are used in more critical calculations, for
example in Sec. 11. Back.