


As was noted in Sec. 3.3, a non-thermal population of electrons must also scatter microwave background photons, and it might be expected that a sufficiently dense relativistic electron cloud would also produce a Sunyaev-Zel'dovich effect. Fig. 11, which shows a radio map of Abell 2163 superimposed on a soft X-ray image, indicates that in some clusters there are populations of highly relativistic electrons (in cluster radio halo sources) that have similar angular distributions to the populations of thermal electrons which are more conventionally thought of as producing Sunyaev-Zel'dovich effects. Indeed, in many of the clusters in which Sunyaev-Zel'dovich effects have been detected there is also evidence for radio halo sources, so it is of interest to assess whether the detected effects are in fact from the thermal or the non-thermal electron populations.

Figure 11. 1400-MHz radio contours superimposed on a soft X-ray image of Abell 2163 (Herbig & Birkinshaw 1995). Note the close resemblance of the radio and X-ray structures, and the diffuseness of the radio source. This is a particularly luminous example of a cluster radio halo source, with a radio luminosity Lradio  1035 h100-2 W. 1035 h100-2 W.
|
Quick calculations based on the Kompaneets approximation (for example, equation 59), suggest that at low frequencies the amplitude of the Sunyaev-Zel'dovich effect should be
so that the effect depends on the line-of-sight integral of the
electron pressure alone. If a radio halo source, such as is seen in
Fig. 11, and the cluster gas which (presumably)
confines it are in approximate pressure balance, then this argument
would suggest that the thermal and non-thermal contributions to the
overall Sunyaev-Zel'dovich effect should be of similar amplitude if the angular
sizes of the radio source and the cluster gas are similar. Since the
spectra of the thermal and non-thermal effects are distinctly
different (compare Fig. 7 and
8),
the spectrum of the overall Sunyaev-Zel'dovich effect
measures the energy densities in the thermal gas and in the radio halo
source separately. This would remove the need to use the
minimum energy argument
(Burbidge 1956)
to deduce the energetics of the source.
Matters are significantly more complicated if the full relativistic
formalism of Sec. 3 is used. But this is
necessary, since the
electrons which emit radio radiation by the synchrotron process are
certainly highly relativistic and the use of the Kompaneets
approximation is invalid. Thus we must distinguish between the
effects of the electron spectrum and those of the electron scattering
optical depth, but the results of Sec. 3.3 can be
used to predict the expected Sunyaev-Zel'dovich effect intensity and
spectrum from any particular radio source.
Consider, for example the Abell 2163 radio
halo, for which we assume a spectral index
The dominance of the thermal over the non-thermal effect from the
cluster arises principally from the lower density of relativistic than
non-relativistic electrons. Only a low relativistic electron density
is inferred because of the high efficiency of the synchrotron
process if only a small range of electron energies is present. If the
frequency range of the synchrotron radiation is extended beyond
the 10 MHz to 10 GHz range previously assumed, then the optical
depth to inverse-Compton scattering depends on the lower frequency
limit as
Thus although the original purpose of searching for the non-thermal
Sunyaev-Zel'dovich effect (as was done by
McKinnon et al. 1991)
was to check on the applicability of the minimum energy formula,
it is more appropriate to think of it as a measurement of the minimum
energy of the electrons that produce the radio radiation. Although
limits on this minimum energy can be deduced from the polarization
properties of radio sources, these limits are model-dependent (e.g.,
Leahy 1990),
and an independent check from the
non-thermal Sunyaev-Zel'dovich effect would be useful.
The problem of detecting the Sunyaev-Zel'dovich effect from non-thermal
electron populations is likely to be severe because of the associated
synchrotron radio emission. At low radio frequencies, that synchrotron
emission will easily dominate over the small negative signal of the
Sunyaev-Zel'dovich effect. At high radio frequencies, or in the mm-wave
bands, there is more chance that the Sunyaev-Zel'dovich effect could be
detectable, but even here there are likely to be difficulties separating
the Sunyaev-Zel'dovich effects from
the flattest-spectrum component of the synchrotron emission.
Several inadvertent limits to the non-thermal Sunyaev-Zel'dovich effect are
available in the literature, from observations of clusters of galaxies
which contain powerful radio halo sources (such as Abell 2163) or
radio galaxies (such as Abell 426), but few detailed analyses of the
results in terms of the non-thermal effect have been possible, and a
treatment of the interpretation of the Abell 2163 data is deferred
until later (Sec. 9.2).
Only a single intentional search for the Sunyaev-Zel'dovich effect from a
relativistic electron population has been attempted to date
(McKinnon et
al. 1991),
and that searched for the Sunyaev-Zel'dovich effect in
the lobes of several bright radio sources. No signals were seen, but a
detailed spectral fit of the data to separate residual synchrotron and
Sunyaev-Zel'dovich effect signals was not done, and the limits on the
Sunyaev-Zel'dovich effects
(of y
One difficulty with the analysis given above, and the discussion of
the testing of minimum electron energy or the minimum energy
formalism, is that radio sources are expected to be strongly
inhomogeneous, so single-dish Sunyaev-Zel'dovich effect observations are
averaging
over a wide variety of different radio source structures (such as
lobes and hot spots). This would mean, for example, that the spectral
curvature that might be predicted by a superposition of the source
spectrum and the Sunyaev-Zel'dovich effect might be also be produced by small
variations in the electron energy distribution function from place to
place within the radio source. If strong tests of the electron energy
distribution are to be made, the observations must be made with angular
resolution comparable with the scale of structures within the radio
sources. For all but the largest radio sources (such as the lobes of
Cen A), this means that interferometers (or
bolometer arrays on large mm-wave telescopes) must be used. No work of
such a type has yet been attempted, and the sensitivity requirements for
a successful detection are formidable.
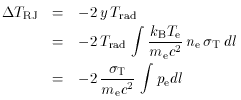
 = -1.5 (there is no
information on the spectral index, since the
halo has been detected only at 1400 MHz:
= -1.5 (there is no
information on the spectral index, since the
halo has been detected only at 1400 MHz:  = -1.5 is typical
of radio halo sources). The diameter of the halo is about
1.2 h100-1 Mpc, and the radio luminosity
(in an assumed frequency range from 10 MHz to 10 GHz) is
1035 h100-2 W.
Using the minimum energy argument in its traditional form (see the
review by
Leahy 1990),
the equipartition magnetic
field is about 0.06 h1002/7 nT and the
energy density in relativistic electrons is about 10-15
h1004/7 W
m-3. This estimate assumes that all the particle energy resides in
the electrons, and that the source is completely filled by the
emitting plasma. The equivalent electron density in the source is
ne = 2 x 10-3
h1006/7 m-3,
which is a factor ~ 106 less than the electron density in the
embedding thermal medium and
corresponds to a scattering optical depth of only
6 x 10-9 h100-1/7, which is
certainly much less than
the optical depth of the thermal atmosphere in which the radio source
resides. Although the power-law electron distribution is more
effective at scattering the microwave background radiation than the
intracluster gas, at low frequencies it is found that the predicted
Sunyaev-Zel'dovich effect from the halo radio source electron distribution is
= -1.5 is typical
of radio halo sources). The diameter of the halo is about
1.2 h100-1 Mpc, and the radio luminosity
(in an assumed frequency range from 10 MHz to 10 GHz) is
1035 h100-2 W.
Using the minimum energy argument in its traditional form (see the
review by
Leahy 1990),
the equipartition magnetic
field is about 0.06 h1002/7 nT and the
energy density in relativistic electrons is about 10-15
h1004/7 W
m-3. This estimate assumes that all the particle energy resides in
the electrons, and that the source is completely filled by the
emitting plasma. The equivalent electron density in the source is
ne = 2 x 10-3
h1006/7 m-3,
which is a factor ~ 106 less than the electron density in the
embedding thermal medium and
corresponds to a scattering optical depth of only
6 x 10-9 h100-1/7, which is
certainly much less than
the optical depth of the thermal atmosphere in which the radio source
resides. Although the power-law electron distribution is more
effective at scattering the microwave background radiation than the
intracluster gas, at low frequencies it is found that the predicted
Sunyaev-Zel'dovich effect from the halo radio source electron distribution is
 TRJ = -5
nK. This is about 105 times smaller than the
Sunyaev-Zel'dovich effect from the thermal gas.
TRJ = -5
nK. This is about 105 times smaller than the
Sunyaev-Zel'dovich effect from the thermal gas.
 e
e  10-12
h-1/7 (
10-12
h-1/7 ( min / GHz)-13/7 (which would be >> 1 if
the electron spectrum extends down to thermal energies). A
reduction in the lower cutoff frequency of the
spectrum by a factor ~ 103 then increases the estimated
relativistic electron density to the point that the non-thermal
Sunyaev-Zel'dovich effect makes a
significant contribution. Indeed, this strong dependence of
min / GHz)-13/7 (which would be >> 1 if
the electron spectrum extends down to thermal energies). A
reduction in the lower cutoff frequency of the
spectrum by a factor ~ 103 then increases the estimated
relativistic electron density to the point that the non-thermal
Sunyaev-Zel'dovich effect makes a
significant contribution. Indeed, this strong dependence of
 e on
e on  min or, equivalently, on the minimum
electron energy, suggests that the non-thermal Sunyaev-Zel'dovich effect is a
potential test for the low-end cutoff energy of the relativistic
electron spectrum.
min or, equivalently, on the minimum
electron energy, suggests that the non-thermal Sunyaev-Zel'dovich effect is a
potential test for the low-end cutoff energy of the relativistic
electron spectrum.
 2 x
10-3 for the best two sources) do not
constrain the electron populations in the radio lobes strongly: the
lobes could be far from equipartition without violating the Sunyaev-Zel'dovich
effect constraint.
2 x
10-3 for the best two sources) do not
constrain the electron populations in the radio lobes strongly: the
lobes could be far from equipartition without violating the Sunyaev-Zel'dovich
effect constraint.